yes, when weight is an issue. No one wants to cart around a heavy amp.
yes, when size is an issue, bigger heatsink bigger enclosure.
Thank you for the input so far.
Intuitively, I can see why one would think that it takes more time to reach thermal stasis with a bigger heatsink: more material to heat up. But is this what really happens?
Also theoretically speaking: if you forget size/mass for a second and think in Rth only, an infinite heatsink would have a Rth of 0, right? Would that not mean that it's impossible to change the temp of the heatsink leading to a thermal stasis almost right from the start (determined by the small Rth of junction to heatsink)?
OK, back to practical applications: I see what you are saying. Once the heat has been transferred to the heatsink, it's dissipated so quickly that the Vbe multiplier senses a lower temp than what the output devices actually are. Due to the different Rths the temp is "divided" much like voltage in a voltage divider.
However, I think the heat resistance from junction to case to heatsink is just too small to become even close to an issue in practical designs, with the possible exception that elvee mentions.
Good point.
Size and cost are disregarded in this discussion. I'm only interested in the thermal and electronic issues.
Merely theoretical jive, but a Class A power amp with an infinite size heatsink is pretty unsmart.
(any amp that doesn't reach thermal stasis in less than an hour is unpractical, save for folks who do not hear a difference anyway)
Intuitively, I can see why one would think that it takes more time to reach thermal stasis with a bigger heatsink: more material to heat up. But is this what really happens?
Also theoretically speaking: if you forget size/mass for a second and think in Rth only, an infinite heatsink would have a Rth of 0, right? Would that not mean that it's impossible to change the temp of the heatsink leading to a thermal stasis almost right from the start (determined by the small Rth of junction to heatsink)?
OK, back to practical applications: I see what you are saying. Once the heat has been transferred to the heatsink, it's dissipated so quickly that the Vbe multiplier senses a lower temp than what the output devices actually are. Due to the different Rths the temp is "divided" much like voltage in a voltage divider.
However, I think the heat resistance from junction to case to heatsink is just too small to become even close to an issue in practical designs, with the possible exception that elvee mentions.
Good point.
Size and cost are disregarded in this discussion. I'm only interested in the thermal and electronic issues.
Last edited:
thermal stasis
Being a layman when it comes to thermal dynamics I wonder how thermal stasis is reached.
Is it a linear curve or does it look more like the curve of charging a capacitor through a resistor (RC-time)? And how would changing the heatsink size affect that curve?
Being a layman when it comes to thermal dynamics I wonder how thermal stasis is reached.
Is it a linear curve or does it look more like the curve of charging a capacitor through a resistor (RC-time)? And how would changing the heatsink size affect that curve?
It is exactly the same as RC curve.
The 'R' is the Rth to the air, which is a defined parameter for the heatsink.
The 'C' is heat capacity, i.e. material 'specific heat' multiplied by its weight.
Note that the unit of Rth*C is:
(K/W)*(J/K)=J/W=s
So it is a time constant as expcted 😉
The 'R' is the Rth to the air, which is a defined parameter for the heatsink.
The 'C' is heat capacity, i.e. material 'specific heat' multiplied by its weight.
Note that the unit of Rth*C is:
(K/W)*(J/K)=J/W=s
So it is a time constant as expcted 😉
Don't be so sure: for a 2N3055, the instability threshold is already reached at a power level of only 8W.
But what does this mean, in practical terms, for a design using this transistor? Can a heatsink be too big in this case?
In theory and massive black anodised heatsink sitting in some hot sun light being used to cool some dinky with amplifier will be kept hot from the sun?
Fans like the Arctic Cooler shown above can be incredibly quiet when run slow. A little air flow can make a huge difference to thermal performance.
Power that is being supplyied gets equal to the power beeing dissipated including infrared radition, convection taking into account matters of the boundery layer on a hetsink fins.
If you are related to aerospace industry and have something like ANSYS handy you might model that.
Except the size you need to take into account how metal distributed in the heatsink (shape) and what metal actually is used.
Unless you gonna manufacture something in thousands quantities where sophisticated modeling could save your funds on a metal in heatsinks (metal is getting pricey especially if it’s going to be copper) by precise layout I would abandon such idea and will use just simple estimation of a heatsink that would let you run a device safely.
Let us try to illustrate the situation with a practical example: put your 2N3055 on an infinite heatsink, and connect a perfect 50V source between emitter and collector (internal resistance=0, no current limitation).
Place a perfect ammeter in series to monitor the collector current.
Then, connect a perfect variable source between base and emitter.
Below ~0.5V, little will happen. If you increase the voltage, you will begin to see a collector current, quickly increasing with the B-E voltage: for each 26mV increase, the current will rise by 2.718x.
But when you approach 160mA Ic, you will notice that the control becomes more and more effective: tiny Vbe increases will generate increasingly high Ic increases.
Finally, when you reach 160mA (=8W Pc), you'll pass the tipping point, and the transistor will be almost instantly destroyed.
Note that in the configuration outlined, this will happen regardless of the size of the heatsink.
But in the real world, there will be some mitigating mechanisms, plus a thermal compensation.
If this thermal comp is made ineffective by a too large heatsink, the thermal runaway will occur, but at a higher power level.
The (simplified) calculations in the previous post show that this can occur at very modest power levels if no degeneration is provided, which is why designs using no degeneration end up in smoke, sooner or later.
Last edited:
Hi Elvee, I am not sure if you and Cordell are describing the same Thermal Runaway Mechanism.
Could you read Cordell and confirm, or otherwise, if you are on the same page?
This confirms you and Cordell are on the same page.
This shows that you already know that the infinite heatsink is not contributing to the problem.
It's as described by Cordell. There is a relationship between Rth j-c and emitter resistor and Vce. Not heatsink.
Last edited:
Adam,
didn't you mean cable sleeve crimping pliers ?
(almost ashamed to admit i bought a ladida WBT sleeve&pliers set within a year after it hit the shops)
I am not aware of Cordell's opinions on those matters.
This is in the "thought experiment" outlined.
In a real circuit, there will be compensations and degeneration mechanisms, explicit or implicit.
All of this will tend to raise the runaway threshold, and make it conditional.
If the thermal sensor is shunted by an extremely low heatsink thermal resistance, it will react very little and with a large lag to the variations of dissipation in the transistor.
This means that a large thermal transient could be sufficient to cross the stability limit.
This thread is indeed meant mostly as a theoretical discussion. And as such elvee's thought experiment is a valid one. I can see the point that when the circuit solely relies on thermal compensation to prevent thermal runaway that too big a heatsink could create problems. However, I'd like to focus a bit more on real world circuits.
In my first thread on this forum anatech mentioned something about not heatsinking ICs with chip heaters (http://www.diyaudio.com/forums/solid-state/39736-intermittent-amp-problem-pm80se.html#post473034).
Are there other reasons to keep the size of the heatsink limited?
It is not the heatsink that is causing the thermal stability problem. Not even when it is infinite.
It is the speed that heat can get away from the junction.
Cordell explains all.
It's in his mosFET interview. Yes he digresses to explain BJTs.
It is the speed that heat can get away from the junction.
Cordell explains all.
It's in his mosFET interview. Yes he digresses to explain BJTs.
It is.
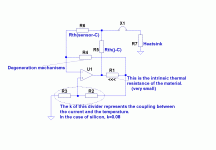
Here is a simplified static model of the situation:
When X1 is closed, the NFB of the system is decreased, and if it falls under 0.08, the positive feedback inherent in the transistor dominates, and the system becomes unstable, unless there are other means of adding NFB, like degeneration resistors.
This means that a system stable with a small heatsink could go into thermal runaway with a larger heatsink.
Intuition is a good guide.
Sometimes.
Here is some training "à la Lewis Caroll", to try to believe impossible things:
Attachments
Yes, Elvee has put his finger on the problem.
There are two mechanisms at work.
One is the internal thermal resistance which becomes dominant if the heatsink is too big. The other is the problem of practical thermal compensation. This problem is really simple to visualize - the definition of an 'infinite heatsink' is that the heatsink temperature does not rise no matter how much power is dissipated. By definition, this means that any rise in die temperature casuses NO rise in heatsink temperature. If so, an external thermal compensation element looking at heatsink temperature as an indication of die temperature will of course see no difference in temperature to compensate, hence result = thermal runaway.
In practice, this will occur with quite realistic sized heatsinks if the thermal resitances from die (of transistor) to die (of the thermal sensor) is sufficiently different at any given boundary. Example which is close to the 'infinite heatsink' thought experiment, is a huge heatsink on which you have a active element and compensation element, with Rth high with respect to Rth of the heatsink to air. The heatsink will be an attenuator and inertia component from active element to NFB element. While you can battle attenuation with gain, you cant make time go backwards - the heatsink imposes a time constant into the control loop which may be longer than is required for destruction by runaway at some operating point- hence, there is danger of destruction.
Last edited:
- Status
- Not open for further replies.