A loudspeaker engineered for single-ended triode amplifiers
 This article follows the design process from theory to measurement of a loudspeaker engineered to be driven by a low powered single-ended triode amplifier. The author has a broadcast background, so accuracy was a key requirement. This is not a loudspeaker designed to sound “nice”, it is a loudspeaker engineered to sound “right”.
This article follows the design process from theory to measurement of a loudspeaker engineered to be driven by a low powered single-ended triode amplifier. The author has a broadcast background, so accuracy was a key requirement. This is not a loudspeaker designed to sound “nice”, it is a loudspeaker engineered to sound “right”.Some Loudspeaker History
In the early 70s, a landmark series of JAES papers written by A N Thiele and R H Small blew away decades of empiricism and put the relationship between a loudspeaker and its enclosure on a firm engineering footing. At the same time, the cheaper and lighter transistor had usurped the valve, and transistor power amplifiers quickly settled down to variations of the H C Lin circuit. Between them, these two events defined an unspoken assumption that has underpinned loudspeaker design for the last forty years.
The Thiele and Small papers showed that a loudspeaker in an enclosure was analogous to an electrical high pass filter and could therefore use electrical techniques to model bass response. Crucially, it was shown that the Q of the bass high-pass filter was determined primarily by the flux density in the gap and the sum of voice coil resistance and amplifier source resistance.
The vast majority of transistor audio power amplifiers use sufficient voltage negative feedback to ensure that their output resistance is essentially zero, and since most amplifiers are transistor, loudspeaker designers since the 70s have assumed that their designs will be driven from zero source impedance.
Single-ended triode amplifiers
Just as the early 80s saw a renaissance of push-pull valve amplifiers, the late 90s saw the reappearance of an even earlier technology – the single-ended triode amplifier. From the point of view of a loudspeaker, the defining characteristics of a single-ended amplifier are:
- Low power – usually < 8W (300B), often 4W (2A3)
- Non-zero output resistance – typically one third to one half load resistance
Dealing with the low power characteristic first, we need an efficient loudspeaker. According to Small(1) the reference efficiency of a closed box loudspeaker is:
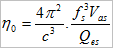
Where:
η0 = reference efficiency
c = velocity of sound in air (≈ 344m/s at 20°C)
fs = loudspeaker free air resonant frequency
Vas = enclosed volume of air having the same compliance as the driver’s suspension
Qes = Q of driver considering voice coil DC electrical resistance RE only
Noting that the first term is a collection of physical constants, this fundamental equation shows us that (all other factors being equal) loudspeakers with a low Qes are more efficient. It’s not explicit, but it also says that you can forget any idea of combining bass extension and efficiency without a box the size of a refrigerator – that f3 term means that bass costs dearly.c = velocity of sound in air (≈ 344m/s at 20°C)
fs = loudspeaker free air resonant frequency
Vas = enclosed volume of air having the same compliance as the driver’s suspension
Qes = Q of driver considering voice coil DC electrical resistance RE only
Turning to the amplifier’s non-zero source resistance characteristic, we will see shortly that although a low Qes is desirable for efficiency, we typically need a somewhat higher value of Qe to shape the loudspeaker’s bass response correctly. However, Qe takes account of amplifier source resistance:
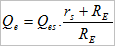
Where:
Qe = Q of driver including all electrical resistances
Qes = Q of driver considering voice coil electrical resistance RE only
rs = amplifier source resistance
RE = loudspeaker voice coil DC resistance
The previous equation is a very happy result because it means that by marrying a high efficiency loudspeaker (low Qes) to a low powered amplifier having significant output resistance (rs) it is possible to achieve the required value of value of Qe. Qes = Q of driver considering voice coil electrical resistance RE only
rs = amplifier source resistance
RE = loudspeaker voice coil DC resistance
Driver choice and the significance of efficiency
The Fostex FE166E data sheet suggests a reasonably flat response up to 20kHz and a claimed efficiency of 94dB/W at 1m with low Qes, so this full range driver was chosen. Typical “bookshelf” loudspeakers (usually actually mounted on stands away from boundaries) have an efficiency of ≈ 86dB/W. 8dB may not sound much, but in power terms it is a factor of 6.3, meaning that a 4W amplifier driving the FE166E would be as loud as a 25W amplifier driving an 86dB/W loudspeaker.
Boxes, and Thiele & Small
Loudspeakers are a collection of compromises and one balance to be struck is in the bass response. Any loudspeaker can be considered to be a high-pass filter, and since it is impractical (read “very expensive”) to engineer the cut-off frequency of this filter to be below the audio band, we are forced to live with its audible effects. The transfer function of the high-pass filter that describes a closed box system is:
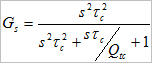
Where:
s = jω
τc = the time constant of the filter
Qtc = the Q of the filter
The key parameter that determines the shape of loudspeaker bass response in the cut-off region is the Q of the 12dB/octave high-pass filter formed by the loudspeaker in its enclosure, Qtc. See Fig. 01.τc = the time constant of the filter
Qtc = the Q of the filter
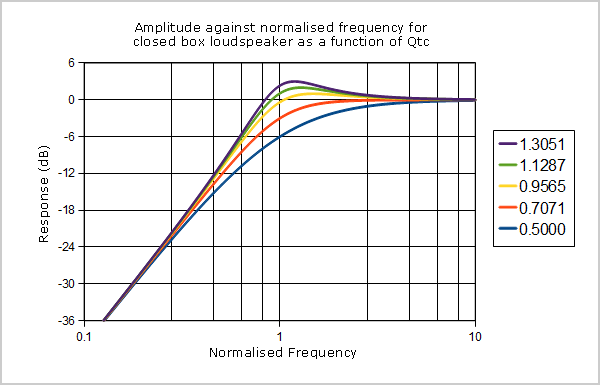
Figure 1: The effect of Q on bass.
Bass sells boxes, so all designers seek to optimise the bass response, but there are different definitions of “optimum”. Starting from a given driver, some feel that the most important goal is to lower the f-3dB cut-off frequency, so they might slightly underdamp the response (Qtc = 0.9565) to give a 1dB peak in the bass above the cut-off frequency – not only does this significantly lower the f-3dB cut-off frequency, but the subjective effect of that 1dB peak is that the cut-off frequency has been even further reduced. Sadly, many designers of small boxes take the underdamped approach too far, allowing peaks of 3dB or more in an effort to exploit the subjective effect. Most prefer a vented or “reflex” box to a closed box, trading transient response for bass extension, with the further option of adjusting damping. Designers having the luxury of a large box and a more discerning customer might prefer to concentrate on transient response and critically damp their loudspeaker (Qtc = 0.5) – calculating that room gain at low frequencies will result in a correct composite response.
Space is too short to fully reprise all the competing techniques, so the author will simply state that vented boxes rely on a Helmholtz resonator requiring time for its amplitude to build and decay. To the author’s ears this makes vented box bass a two-part affair consisting of a clicking transient followed a fraction of the beat later by bass weight. For a given loudspeaker, the compromise is between lowering the cut-off frequency and optimising the transient response. The Arpeggio veers further towards optimising transient response than is usual for this size of box, leading to a closed box having a maximally flat amplitude response (Qtc = 0.7071).
Determining box volume from Qtc
From the Fostex FE166E data sheet:

The primary design specification for the Arpeggio was that it should work correctly when driven by an amplifier having a 6.5Ω source resistance, so we must calculate the effect of this non-zero source resistance on the loudspeaker’s electrical Qe:
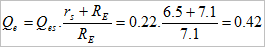
Combining electrical Qe and mechanical Qms is similar to connecting resistors in parallel:
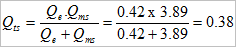
Rearranging Small’s equations(2), the required box volume is:
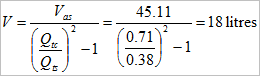
And the predicted f-3dB frequency of the loudspeaker/box combination, fc is:
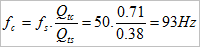
There is plenty of software available for modelling loudspeaker enclosures and plotting informative curves, but the effect of the non-zero source resistance rs generally has to be calculated manually.
But my amplifier’s source resistance is < 6.5Ω…
This is not a problem. Simply add series resistance to make it up to 6.5Ω. Perhaps you have a 300B single-ended amplifier operating under the traditional conditions of Vak = 400V, Ia = 60mA, and 5kΩ loading to produce 8W. Under these conditions, ra ≈ 800Ω and the DC resistance of the transformer primary Rp ≈ 100Ω, so the output resistance seen at an 8Ω tap would be ≈ 1.5Ω. Thus, a 4.7Ω 5W series resistor would leave an allowance for loudspeaker cable resistance.
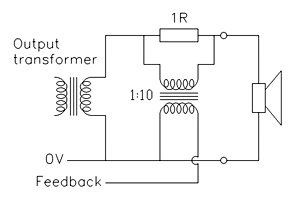
Another way to increase the output resistance of the 300B amplifier would be to add current feedback. In theory, 13dB of current feedback would raise the 1.5Ω output resistance to 6.5Ω, but a 1Ω current sense resistor and an expensive step-up transformer would be required to derive a usefully large feedback signal: See Fig. 02.
In practice, the loss of power caused by a simple 4.7Ω series resistor does not seem to be a problem. The author has driven his Arpeggios from his “Scrapbox Challenge” 6528 single-ended amplifier, which has a 2Ω output resistance on its 8Ω tap, so he added the nearest standard value power resistor he had – 4.7Ω, and the 6W amplifier was still able to make the Arpeggios go loud enough for the author to be nervous about cone excursion.
Other effects of non-zero source impedance
Although we have just seen that provided a suitable loudspeaker is chosen, any required bass response can be engineered in spite of a non-zero source resistance, a potential divider is formed by the amplifier source resistance and loudspeaker impedance:
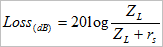
Where:
Loss = attenuation in dB
ZL = impedance of loudspeaker
rs = amplifier source resistance
Unfortunately, practical loudspeakers have an impedance ZL that varies with frequency. See Fig. 03.ZL = impedance of loudspeaker
rs = amplifier source resistance
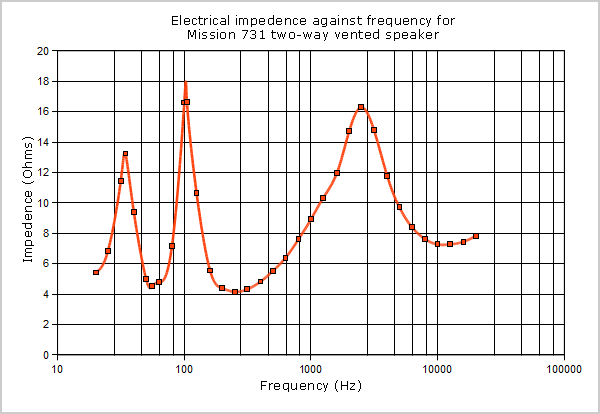
Figure 3: Impedance curve of typical modern loudspeaker.
Despite being specified as an 8Ω loudspeaker, this measurement of the Mission Electronics 731 shows it to be a 4Ω woofer allied to an 8Ω tweeter. This is common practice because:
- It allows a 3dB improvement in apparent sensitivity (dB/W), so the loudspeaker sounds louder, and loudness sells. The 4Ω woofer actually consumes twice as much power as advertised, but a modern transistor amplifier is a voltage source and perfectly capable of driving a 4Ω load at low to medium frequencies.
- Tweeters are typically 3dB more sensitive than woofers. This imbalance could be equalised by adding a series resistor, but a more elegant method is simply to redesign the tweeter for double the impedance and benefit from reduced amplifier distortion at high frequencies due to increased load impedance.
Unfortunately, as will be demonstrated, a single-ended triode amplifier would be most unsuitable for this class of loudspeaker. In order to minimize amplifier distortion, the single-ended triode amplifier would have to treat the loudspeaker as a 4Ω load, so it could have anything up to a 2Ω source resistance, modifying the electrical response at the loudspeaker terminals and thereby deviating from the loudspeaker designer’s response. See Fig. 04.
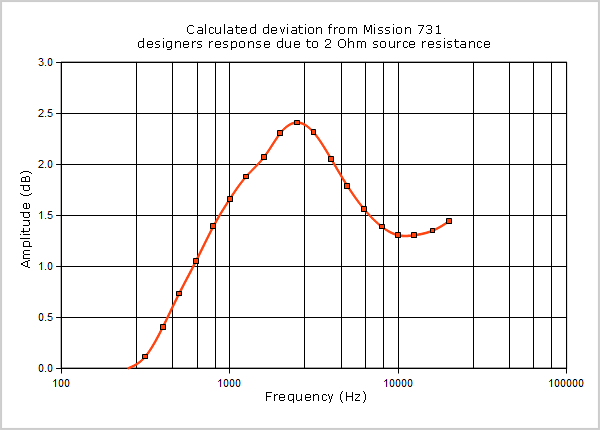
Figure 4: Frequency response error caused by 2Ω source resistance.
Note that the effect of the non-zero source resistance is to produce a 2.4dB peak at the ear’s most sensitive frequency (2-3kHz) followed by a +1.3dB shelf to 20kHz. The effect on the bass response has not been shown because it does not follow directly from the electrical response at the loudspeaker terminals, but a bass peak can be expected. Summarizing, any loudspeaker designed to be driven from zero source resistance will exhibit deviations from the designer’s response if driven from a non-zero source resistance.
Below 2.5kHz, the rise in impedance is caused by woofer voice coil inductance, and above 2.5kHz, the fall in impedance is caused by the crossover beginning to connect directly to the tweeter. The two effects combine to produce a peak at 2.5kHz, so a peak of this form is always indicative of a crossover. It is possible to engineer a crossover having constant input impedance, but it is expensive, so the idea has not become popular.
Avoiding the need to compensate for the crossover impedance peak was a major factor in the choice of a full range loudspeaker for the Arpeggio – compensating for the voice coil inductance of a single driver can be achieved simply and efficiently.
The Zobel network
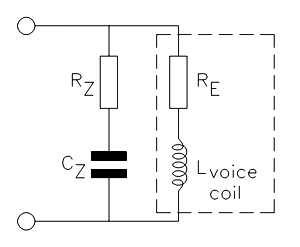
Above low frequencies (> 250Hz) the electrical impedance of any moving coil cone loudspeaker may be represented by the series combination of its voice coil DC resistance and inductance. If we add the complex conjugate of this impedance in parallel (known as a Zobel network), we can correct it to a constant resistance. See Fig. 05.
In theory, the Zobel resistance RZ is equal to the loudspeaker’s RE, and the capacitor value is found using:
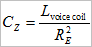
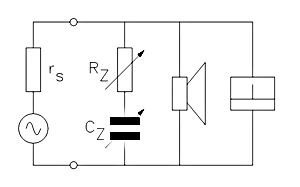
In practice, transformer coupling from the voice coil to the shorted turn of the steel pole pieces either side of the gap means that RZ is typically empirically multiplied by a factor of 1.2. Alternatively, values for RZ and CZ can both be found experimentally using a starting point of RZ = 1.2RE plus a decade capacitance box together with a variable frequency oscillator and meter as shown. See Fig. 06.
The output resistance of the oscillator and the Zobelled loudspeaker form a potential divider whose output is measured by the meter. A good source resistance is 100Ω, but this value is not critical. Ideal Zobel values produce minimal change in the meter reading as oscillator frequency is swept. Note that most DVMs are only designed to measure 60Hz AC and have large errors above this frequency, so a dedicated audio meter is usually best.
Using the previous setup, suitable values for an FE166E were; RZ = 10Ω and CZ = 5.16μF (4.7μF in parallel with 0.47μF is quite close enough). The author used a hot-melt glue gun to glue the capacitors directly to the loudspeaker’s magnet, then soldered a non-inductive 5W thick film resistor to the capacitors and hard-wired this combination to the loudspeaker terminals. See Fig. 07.
Adding this Zobel network produced the electrical effects shown in the graph. See Fig. 08.
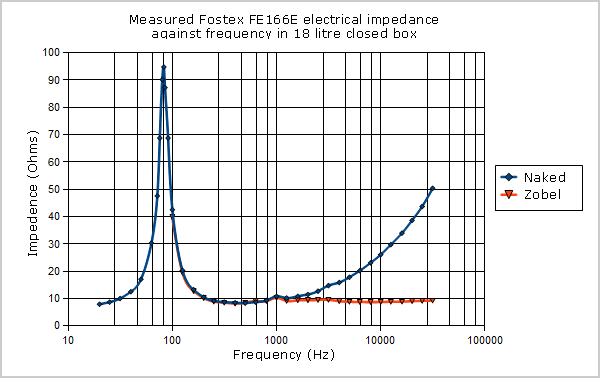
Figure 8: Comparison of loudspeaker impedance with and without Zobel network.
As can be seen, the corrected driver has a very nearly constant resistance of ≈ 9 Ω above 200Hz. The slight blip at 1kHz is not a measurement error but is thought to be a dust cap/voice coil mechanical resonance being coupled back into the electrical impedance. The impedance peak at 83Hz is electrical confirmation of the system’s mechanical resonance and is a good indicator for any system of the lowest frequency that can be reproduced without equalisation.
Baffle dimensions and diffraction
Having determined the Arpeggio’s internal volume it is time to consider that box’s practical dimensions and it should come as no surprise to learn that the size and proportions of the front panel (baffle) are significant. What undoubtedly will surprise the reader is that most loudspeakers have sub-optimal proportions…
At low frequencies, the radiation of sound from a loudspeaker is omnidirectional, so what happens when sound travels across the front face of the box and reaches the edges? The edges are a discontinuity and cause a reflection that interferes with the outgoing wave – this phenomenon is known as diffraction and the reflection is commonly known as a secondary source.
Consider the very worst possibility of a loudspeaker mounted centrally on a circular baffle. The distance from the loudspeaker to the edge is the same for all angles and there will be a frequency for which the time taken for the wave to travel to the edge of the baffle and back corresponds to half a wavelength, so the returning wave is of opposite polarity to the outgoing and they cancel. Similarly, there will be another frequency for which the time taken for the reflected wave to return corresponds to a whole wavelength, so the two waves are of the same polarity and sum constructively. Further, both of these effects can and do occur at multiples of their fundamental frequency, so the complete response is that of a comb filter. See Fig. 09.
We must minimise the effect of this comb filter, and this can be done in a variety of ways arranged in descending order of effectiveness:
(1) Maximise the distance from the loudspeaker to the baffle edge. This lowers the frequency of the first null and thus moves the harmonics of that null closer together, perhaps rendering them indistinguishable or susceptible to some other treatment.
(2) Blur the distance to the baffle edge. Our initial example of a circular baffle had a very sharply defined single distance, but if we were to make that distance variable by placing the loudspeaker in the centre of a square baffle, then some paths would cancel when others summed constructively.
(3) Break the symmetry. The square baffle had a rotational symmetry because each quadrant was identical. We gained an improvement from the circular baffle by breaking an infinite symmetry to four, but if we were to move the loudspeaker from the centre there might be a position where there was no symmetry (one).
(4) Attenuate the wave before reflection. If there is no secondary source then there can be no cancellation and summation.
(5) Blur the edge. Rather than having a sharp edge with an abrupt change of acoustic impedance, the edge could be rounded – this technique is arguably a subset of (2).
The obvious way of achieving (1) is to use a very large baffle, but this tends to be impractical. Nevertheless, some recording studios achieve a good approximation by recessing monitoring loudspeakers so that their baffles are flush with the wall. Similarly, some older cinema systems used very large baffles concealed behind the (large) screen. Both of these approaches necessarily invoke (2) and with thoughtful design may invoke (3).(2) Blur the distance to the baffle edge. Our initial example of a circular baffle had a very sharply defined single distance, but if we were to make that distance variable by placing the loudspeaker in the centre of a square baffle, then some paths would cancel when others summed constructively.
(3) Break the symmetry. The square baffle had a rotational symmetry because each quadrant was identical. We gained an improvement from the circular baffle by breaking an infinite symmetry to four, but if we were to move the loudspeaker from the centre there might be a position where there was no symmetry (one).
(4) Attenuate the wave before reflection. If there is no secondary source then there can be no cancellation and summation.
(5) Blur the edge. Rather than having a sharp edge with an abrupt change of acoustic impedance, the edge could be rounded – this technique is arguably a subset of (2).
At the other end of the scale, the classic BBC LS3/5a monitoring loudspeaker was far too small to use (1), and the diameter of the loudspeaker magnets too large compared to the baffle to be able to use (3), so the designers had to use (4) by adding strips of absorbent felt to the front face of the tweeter. See Fig. 10.
Many modern loudspeakers radius the edge of the baffle, but as this radius is typically only 20mm it is arguable that the effect is mainly cosmetic – 100mm radius would be better to fully invoke (5).
However, the most alarming discovery that falls out of this analysis is that most modern loudspeakers neglect (1) and (3) by mounting their drivers centrally at one end of a slim baffle. Undoubtedly, this has been forced upon loudspeaker designers by the two facts of decreasing living space and increasing consumer goods to fill that space, but it is still an unwelcome compromise – look back to the early 60s when loudspeakers were big shallow affairs with a large frontal area.
Our task is to choose baffle proportions and driver positioning so as to maximise the effect of (2) and (3) whilst easing the requirement for (1). If necessary, we might apply (4) and (5) to tidy remaining defects, but baffle size and proportions are key. Fortunately, we are in possession of far better design tools than the 60s designers and can model baffle diffraction using software based on finite element analysis. Essentially, such models break the baffle into many simple elements, calculate the response at each element, then sum the elements to give a composite response.
Using a baffle diffraction simulator such as “The Edge”
There are undoubtedly many baffle diffraction simulators available, and as with any model, the important factor is understanding that model’s limitations. Browsing diyAudio led to the discovery of “The Edge” software at Home of the Edge. Not only is the software intuitive to use (even by this Luddite) but its predictions generally agree with measurement. The webpage has the facility for users to donate a small sum of money to the software’s author and this writer would strongly urge that you do so too.
Having chosen to use a single Fostex FE166E, the cone diameter is set and we have freedom to choose baffle dimensions and driver positioning. Even if we restrict ourselves to a rectangular baffle, this makes for a four dimensional problem. Fortunately, we can greatly reduce the design complexity by making two important observations:
- The worst form of rectangle would be a square because it doesn’t break the symmetry between top to bottom and side to side, so all the peaks and nulls in the “x” axis exactly match the peaks and nulls in the “y” axis. Ideally, the “x” axis should not harmonically relate to the “y” axis, and the Golden Ratio of 1.618 might be a good starting point for relative “x” and “y” dimensions.
- The distance of the driver to each of the four edges should be as disparate as possible and avoid harmonic relationships. This tends to mean that the optimum driver position is pushed as far as possible into one corner.
Symmetry means that there is no difference between one corner of a rectangular box and any other corner, so the problem is most conveniently modelled by placing the driver as far into the bottom left corner as reasonably practicable (bearing in mind box wall thickness and driver cut-out), then adjusting baffle dimensions in the “Baffle size” box. The software includes a tick box to enable “baffle step compensation” and we will explore this topic in a moment, but suffice to say that it is easiest to view the effect of changing box proportions with this option enabled.
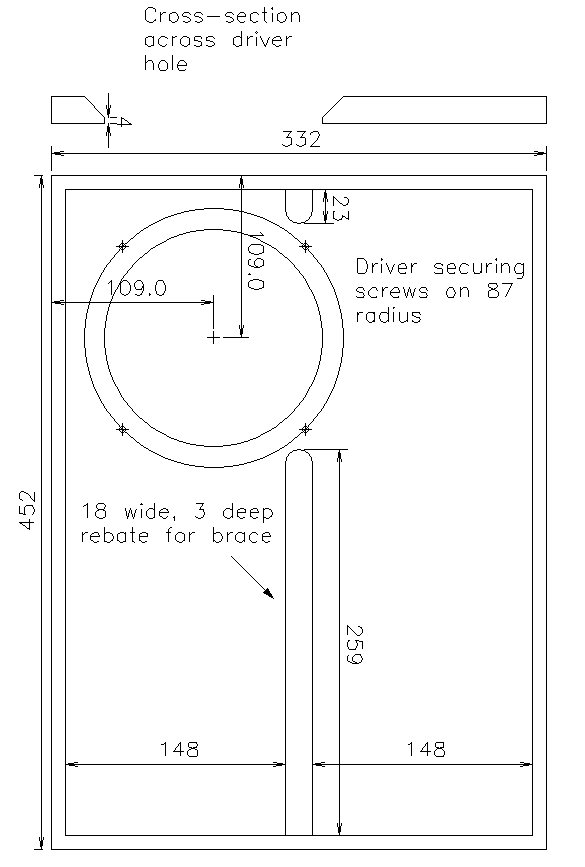
The author’s target was to reduce ripple in the on-axis response to < 1dBpk-pk because ripple cannot be equalised whereas gentle trends can. Thus, the driver was positioned in the corner with its centre 108mm from each edge and baffle dimensions of 330mm x 450mm gave a simulated response that looked equalisable. See Fig. 11.
Baffle step
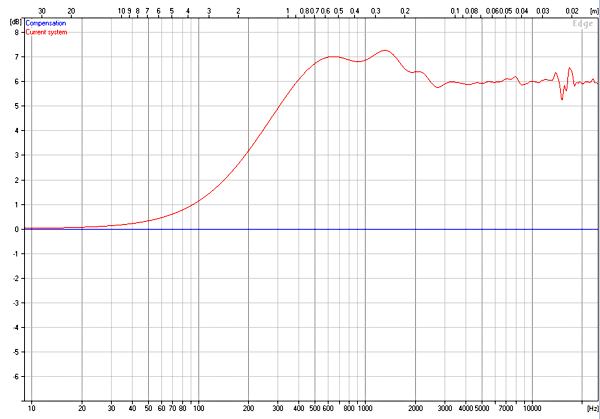
Having settled on baffle size and loudspeaker positioning on that baffle, it is instructive to disable the baffle step compensation and reduce the modelled frequency to well below what the system could actually reproduce. See Fig. 12.
We see a predicted 6dB step in the response because as wavelength falls to become comparable with the dimensions of the box, the loudspeaker no longer radiates into the full volume of a sphere (often known as 4π space) but into only half that volume (2π space), doubling the sound pressure level (SPL). This effect is commonly known as baffle step.
In terms of frequency, the position of baffle step is determined by the size of the baffle, so the ideal would be to make the baffle sufficiently large that baffle step occurs below the system cut-off frequency. This is because any baffle step within the loudspeaker’s pass-band must be equalised electronically, costing amplifier power and loudspeaker distortion. The combination of these two reasons was another factor that led to the chosen baffle dimensions.
From an engineering viewpoint, the best place to apply baffle step equalisation is at the input to the power amplifier, but this makes selling loudspeakers more difficult, so commercial loudspeakers are forced to use an inductor in series with the loudspeaker. The disadvantage of applying baffle step equalisation after the power amplifier is that it wastes amplifier power. Conversely, placing the equaliser before the power amplifier gives two advantages:
- The power amplifier only has to provide as much power as the loudspeaker actually needs. At frequencies above a 6dB equaliser the amplifier is required to deliver 6dB less power – for a single-ended triode amplifier this translates directly into 6dB less amplifier distortion for a given sound intensity.
- With a few exceptions, most music does not require as much power at bass frequencies as elsewhere. Placing a 6dB baffle step equaliser before the power amplifier would allow almost any amplifier/loudspeaker combination to play a string quartet 6dB louder before amplifier clipping than if the equaliser was placed between the power amplifier and loudspeaker. This is a significant advantage for a low power amplifier.
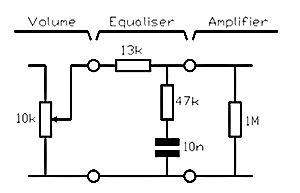
Passive baffle step equalisation at the input to the power amplifier requires a shelf equaliser composed of two resistors and a capacitor that set a pair of time constants. The ratio of the time constants sets the amount of equalisation and R1C sets the upper frequency from which equalisation begins. Unfortunately, although the Edge’s model correctly predicted the Arpeggio’s R1C time constant, it predicted R2C incorrectly and 6dB of baffle step equalisation was far too much. Fortunately, it was easy to replace R2 with a tandem potentiometer and adjust until the bass sounded correct. Pleasingly, subsequent measurement confirmed that the 2.4dB setting determined by ear was appropriate.
The theoretical disadvantage of a passive equaliser is that the time constants are sensitive to changes in terminating resistances. In practice, this proves not to be a problem because it is easy to make a valve amplifier’s input resistance 1MΩ and any modern source can easily drive a 10kΩ load (typical volume control value). Thus, all that is necessary is to apportion component values such that the equaliser is tolerant of these resistances. See Fig. 13.
The small amount of equalisation required means that component values are not too critical, making it easy to use standard component values. Nevertheless, believing stereo matching to be important, the author matched a pair of polypropylene film/foil 10nF capacitors to 1% from his stock and used standard 1% metal film resistors. If your multimeter doesn’t measure capacitance you might prefer to buy 1% metallized polypropylene capacitors to ensure good stereo matching.
Box problems
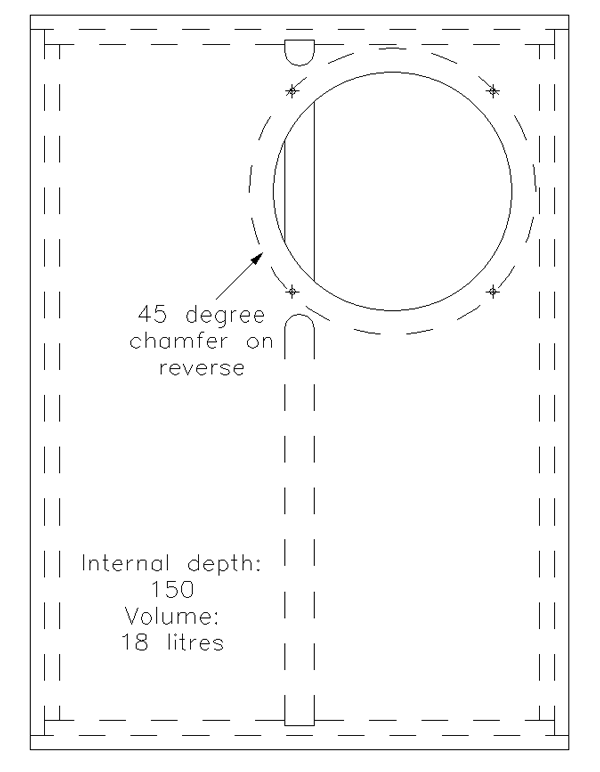
Practical boxes are nasty, and big boxes are even nastier. The problem is panel vibration. The Arpeggio has a box volume of 18 litres and a total box surface area of ≈ 600,000mm2 compared to a loudspeaker cone area of ≈ 13,000mm2 – that’s a ratio of 45 to1. Or to put it another way, if the panels vibrate by only 1/45 of the cone’s travel, they will equal the sound from the cone. Sadly, it is not uncommon for a practical loudspeaker to radiate as much sound from the box as from the cone. It would be hopelessly optimistic to assume that the panels radiate equally energetically at all frequencies, so panel vibration must be restricted as far as possible. In general, it is true to say that the primary difference between a cheap loudspeaker and an expensive one is the attention paid to panel vibration.
There are various ways of tackling panel vibration:
- Make the panel thicker. This popular DIY solution is surprisingly ineffective and using MDF panels > 18mm thick gives very little reward other than allowing better joints between panels.
- Use a lighter, more rigid panel material. Celestion used this approach with the SL600 honeycombed aluminium variant of their SL6 loudspeaker. Mounting drivers onto this material is difficult (read expensive) because although strong, it doesn’t tolerate point loads.
- Surface damp the panel. A BBC-inspired technique was to secure thick bitumastic pads to much thinner plywood panels. One disadvantage is that bitumastic pads harden over the years, reducing their damping.
- Use constrained layer damping. A thin (1-2mm) layer of damping material is sandwiched between two thicker (9mm) layers of MDF. When the panel vibrates it applies a sheer force to the damping material which strongly resists the vibration. JBL tried this extremely effective method of damping panels, but making the composite panel requires a large press, greatly increasing box costs.
- Brace the panel. B&W’s “Matrix” loudspeakers exploit this technique very effectively.
- Make the box smaller. As box size reduces, the panels effectively become better braced. The BBC LS3/5a worked well not so much because it was a good box but because it was a small box.
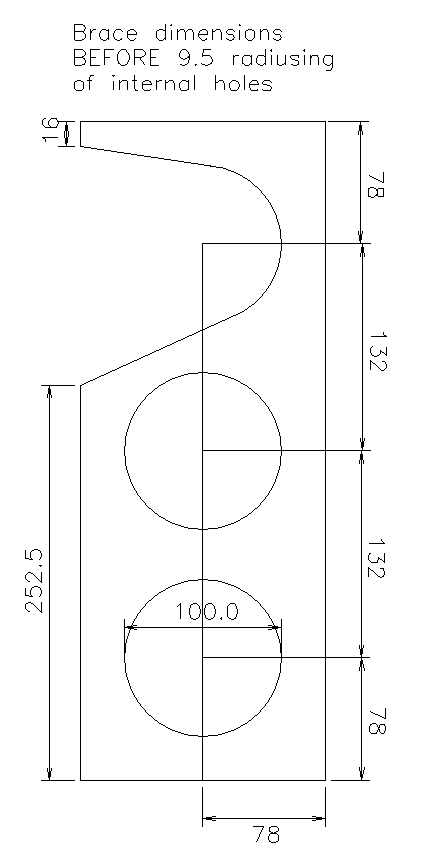
Panel bracing is far and away the best technique but intuition is a very poor guide to effective bracing. Tappan(3) wrote a seminal paper that described how to brace panels effectively. In a nutshell, braces should be applied so as to minimise the diameter of the circle that can be inscribed between adjacent braces (for these purposes, a box wall is defined as a brace). Further, a brace formed of a strip of material is ineffective – the most effective brace is a panel joining opposite walls. Taken together, these two requirements suggest that the most effective bracing is formed by adding panels along the length of the box – which explains why “transmission line” loudspeakers often have a clean lower midrange, it’s nothing to do with the bass loading, more to do with the inadvertent good box.
Because of its proportions, the Arpeggio’s greatest weakness is its large area front and rear panels, so a single vertical panel joining the front to the back is extremely effective. A plain panel could divide the box into a pair of organ pipes, so the panel has large circular cut-outs that prevent pipe resonances without appreciably compromising rigidity.
A lateral thinking method of reducing panel vibration is simply to avoid exciting it. KEF experimented with decoupling the loudspeaker using rubber grommets, but it is difficult to simultaneously achieve adequate decoupling and an effective air seal, particularly if the loudspeaker must point horizontally rather than vertically.
When the cone accelerates it must obey Newton’s laws and apply an equal and opposite reaction to the box. But F = ma, so for a given acceleration, a heavy loudspeaker cone must excite its panel more than a light cone. The Arpeggio’s box is not especially good, but because the loudspeaker cone is so light, it isn’t excited as much. As a general rule of thumb, efficient drivers have lighter cones, making them less effective at exciting panel resonances, reducing box colouration.
Standing waves and fibres
Another box problem relates to standing waves in the air between parallel panels. The worst possible shape would be a cube because all the standing waves would be coincident, so the best possible shape would avoid parallel panels entirely. Many modern loudspeakers have curved panels which not only reduce standing waves but significantly reduce panel vibration because of their greatly increased rigidity. Sadly, curved panels are difficult for home constructors, so the Arpeggio can only reduce standing waves by loosely filling the enclosure with fibrous material.
Fibrous damping works by the air movement bending fibres back and forth and losing energy in each bending cycle. Thus, fibrous damping becomes more effective as frequency rises. To be most effective, the fibres should be placed where air movement is at a maximum, and this means that they should fill the volume of the box, rather than lining the walls. Fortunately, closed boxes can tolerate this placement of fibres whereas vented boxes can’t – another reason the author chose a closed box over a vented box.
The author used long-haired wool rather than bonded acetate fibre (BAF) because he had plenty, but he has no reason to suppose that teased-out BAF wadding would be any less effective in this application.
Breathing
When the cone moves to reproduce a bass note, air must flow through the holes in the loudspeaker basket. Mounting a loudspeaker having a magnet diameter comparable to its cone diameter area in a thick baffle often restricts air flow, causing a loss of clarity in the lower midrange, so it is good practice to use a 45° router cutter to chamfer the inside of the loudspeaker cut-out.
It was allowing for a 45° chamfer in the 18mm baffle that prevented diffraction considerations from moving the loudspeaker centre any closer than 108mm from the Arpeggio’s baffle edges.
Making the box
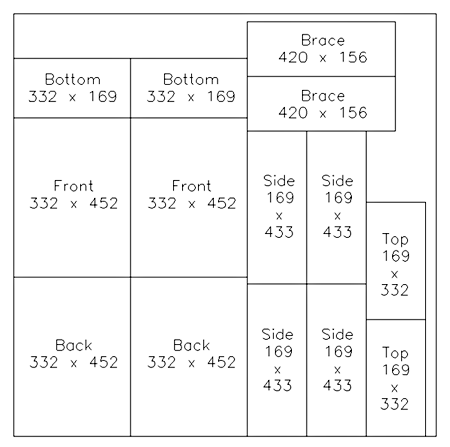
One 1200 x 1200 sheet of 18mm medium density fibreboard (MDF) suffices for a pair of boxes. See Fig. 14.
Placing the driver so close to the corner of the box precludes corner battens, so a rigid jointing method is essential, hence the rebates. A router is essential for this project, together with five standard cutters:
9.5mm rebate
45° bevel
9.5mm radius
≈ 12mm laminate cutter
≈ 12mm standard cutter
All but the last cutter have a ball race on the end to guide the cutter. Individually, cutters tend to be expensive, but a cheap set will almost invariably contain all five of these cutters and more. Since MDF blunts cutters quickly, there is little point in using expensive cutters.45° bevel
9.5mm radius
≈ 12mm laminate cutter
≈ 12mm standard cutter
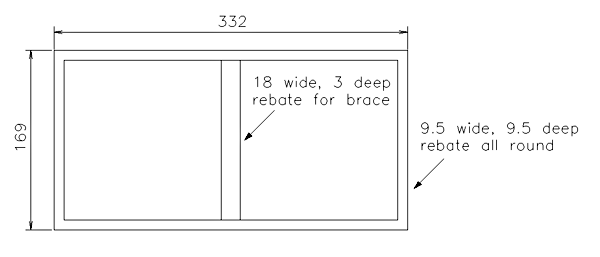
All panels except the internal brace require a 9.5mm wide 9.5mm deep rebate to be routed on all edges on the inside face. When assembled, the box will have slight overlaps at the joints which can be neatly removed with the laminate router cutter – it is for this reason that some panel dimensions appear over-size.
Cut the panels to size and true the edges if necessary. Use the 9.5mm rebate cutter to cut the edge rebate on the inside face of each panel. A router table would make this job extremely easy – so the author bought one. After doing the job using the router hand-held.
Front baffle and rear panel
Note that for best stereo the loudspeakers should be made as a handed pair. One box should have the loudspeaker in the right-hand corner, one in the left; all the drawings refer to the right-handed loudspeaker – simply mirror the driver positioning measurements for the left.
Drill holes in the rear panel to take electrical connectors of your choice behind the driver. Cut the 146mm diameter hole for the driver from the front face using a jigsaw (note that the 109 dimension is not an error; 1mm will be lost from the baffle after assembly). Cutting from the front face means that should the blade bend during cutting, errors will appear on the rear, which will be routed away. Use the 45° bevel cutter from the rear face to chamfer the cut-out to approximately 4mm of the front face. Next, fit the standard cutter and rout the 3mm deep 18mm wide rebates on the front and rear panels. See Fig. 15.
Top and bottom
Rout the 3mm deep 18mm wide rebates on these panels, taking care to ensure that they line up with the rebates on the front baffle and rear panels. It’s useful to uniquely identify each individual panel and its orientation at this point. See Fig. 16.
This panel does not have an edge rebate. Cut the ≈ 100mm diameter holes with a jigsaw, then use the 9.5mm radius cutter from both sides to round them over. These cut-outs do not need to be precise, but the rounding is easy and prevents scratching your hands when filling the box with wool. See Fig. 17.
Assembly
Test fit each box. See Fig. 18.
The panels should fit together snugly and the brace should ensure that the box is square. Check that panels cannot rock on the brace, and conversely, that the brace seats correctly into all the rebates. The easiest way to begin assembling the box is to lay the back panel flat and glue the brace plus top and/or bottom. This minimum combination of panels tends to self-locate because of the morticed joints. If you are really courageous (and have a lot of clamps) you could also glue the sides. You might need assistance to fit and clamp everything fast enough before the glue starts drying. Do not attempt to fit the front baffle at this point. Leave the glue to cure for a day to achieve full strength.
When all the panels but the front baffle have been glued, check that the rebate from one panel lines up with the rebate for the next. If necessary, trim until the front baffle fits firmly and snugly without any rocking. Glue the front baffle. Leave the glue to cure for a day to achieve full strength.
The pair of boxes will now have lips that can be neatly removed by the laminate cutter, although a little sanding will also be necessary. Use the 9.5mm radius cutter to radius the front baffle’s edges.
Decorative finishing
The author has traditionally covered his loudspeakers with Formica phenolic laminate because his woodworking skills permit nothing more adventurous. Furthermore, he has a deep suspicion that gluing hard laminate to MDF with a soft rubbery contact adhesive fortuitously applies constrained layer damping to that panel. This suspicion was founded many years ago when he had applied only the front, back and one side of Formica to a loudspeaker and it was many months before the remaining surfaces were applied. The loudspeaker was playing at the time, and the instant the large side panel was affixed a clear improvement was heard.
If you follow the author’s lead and clad your boxes with Formica, the edge facing the listener of the top, bottom, and sides must be cut perfectly cleanly before affixing to the box. The way to do this is to cut the Formica panels ≈ 5mm oversize (jigsaw with metal cutting blade works well) then clamp four panels of the same size together and use a guide (such as a straight piece of angle) to guide the router to trim the edge using the standard cutter.
Cut the back panels to ≈ 5mm oversize and glue using contact adhesive. Use the laminate cutter to trim excess. If you haven’t done this before, you will be amazed at how neat a job it does. Resist the temptation to run your finger along the beautifully clean edge. It cuts your finger and hurts like a paper cut. The author knows…
Cut and fit the sides, making sure the clean routed edge lines up perfectly with the joint to the front baffle. Trim the other edges with the laminate cutter.
Now that you’re practised, cut the top and bottom (noting that they’re a little larger than you might have expected because they have to extend to the edges of the already fitted Formica. Make sure the clean edge aligns perfectly with the edges of the existing Formica at the corners. Trim with the laminate cutter.
Use 600 grade silicon carbide abrasive paper supported on a scrap of wood to round those sharp edges before you cut yourself.
Felt
Bucking the trend of “any colour so long as it’s black” the author likes bright colours on the front of his loudspeakers, and a convenient way of applying a bright colour is to use felt – especially as it gives a small, but measurable improvement in the off-axis response. The felt is readily available from the haberdashery section of department stores. For the benefit of UK readers, I got mine at John Lewis, but I expect it's all made at the same factory no matter where you buy it. The label says "Superfine felt, 70% viscose, 30% wool. Do not wash, sponge or dry clean". It is 90 cm wide and about 1mm thick. The exact composition and thickness are unlikely to be critical.
On a psychological note, it’s best to avoid blue as it suggests a cold fatiguing sound, whereas red, brown, and black suggest a warmer more relaxed sound. The felt colours you will use are probably darker than MDF, so use a black marker pen on the MDF where it touches the Formica before felting to mask any possible gaps in the join.
A vertical black stripe next to a deep red makes the loudspeaker look smaller and the author has used this on all his successful loudspeakers. It’s up to you, but this design detail is recommended. Mark a clear line on the MDF where the two felt colours are to join. Iron the felt. Being careful not to stretch the felt, use a marker pen to mark a straight line on the felt where that colour will join to the other. Cut along that straight line with dressmaker’s large scissors. Cut the other edges of the felt 20mm oversize and don’t worry about precision edges – their excess will be trimmed later.
Lay masking tape butted up to the front edge of the Formica all round the box to prevent the felt trying to stick to the Formica.
Gluing felt isn’t too difficult, but you do need to get it right first time. Although the glue fumes are unpleasant, if you do the work outdoors any wind will blow the felt so that it sticks to itself. Work indoors with the windows open. The author uses Dunlop “Thixofix” applied using their spreader to the baffle, and 3M “Spraymount” sprayed carefully to the felt. Apply the Thixofix and wait for it to become touch-dry, then spray the felt evenly. The crucial point is to avoid blobs of glue that could soak through the felt.
Fit the larger piece of felt first. Starting at one end of the join line, very lightly tension the felt as you press it down to the line. Then gently press the remainder down to the front surface. Don’t worry about curving the felt over at the radiused edges yet. Now fit the smaller piece of felt, making absolutely sure that it butts up to the first as you position it.
Use the face of a clean steel ruler to press the felt firmly onto and round the corners, and make sure the edge of the ruler presses the felt firmly onto the MDF just before the Formica edge. The felt will be slightly rucked as it approaches the box corners, nevertheless, it can easily be persuaded to glue neatly to the radius between the corners. Use the ruler face to slide along and press the felt down, ensuring that the ruler edge presses into the Formica edge. Be careful when you go over the join between the two colours – and ensure that they butt together neatly.
When you are certain that all the felt has been very firmly pressed onto the glue, it can be trimmed. Using a new curved (№ 10) scalpel blade for each edge cut the felt along the edge of the Formica and gently peel the excess away. If the excess won’t come away easily, repeat the cut – do not force the peeling as the felt will fray. This is easier than it sounds, and the best way to do it to enlist the help of the ruler. Press the flat of the ruler firmly on the felt that must remain and use it to locate the scalpel blade snugly against the edge of the Formica, then slide the ruler, allowing it to move the scalpel. Do not try to move the scalpel independently as it will probably ride up over the Formica (scoring it) or move the ruler and wander into the felt (wrecking it). Start on the bottom edge to get a feel for how the process works. Apply reasonable force to the scalpel and don’t worry about cutting into the MDF, but apply as much pressure as possible to the ruler to make it an effective guide. Replace scalpel blades the instant you suspect they are losing any cutting efficiency – they are cheap.
Cut the hole for the driver with the scalpel. The felt will form a gasket for the driver.
You will note that the description of how to glue and trim the felt is almost as long as the description of how to make the box. This is not because fitting the felt is harder, just that many people are versed in woodwork, but few are practised felt-fitters!
Wiring and wool stuffing
Fit the Zobel network to the driver. Take wires from your terminals to the driver. The driver now needs to be laid on the front baffle and will leave a dent in the felt unless you put a thick piece of cardboard in the way. Tease out ≈ 120g per box of long-haired sheep’s wool (as used in transmission lines) or BAF wadding and completely fill each box. Secure the driver to the box with self-tapping screws, taking care not to let the screwdriver skid and puncture the cone. Pozidriv (Europe) or Philips (America) screws are a good idea. Tighten opposing screws sequentially to avoid distorting the basket.
Final measurements
Detailed explanation of design is all very well, but how well does it work?
Acoustic measurements had to be taken in two parts because the author’s home does not include an anechoic chamber. Not even a little one. Instead, a quasi-anechoic computer-based measurement system was used that removes the effect of room reflections, but needs two different techniques to cover the entire audible range. The first response was measured at the standard measuring distance of 1m by applying a short pseudo-random noise burst and truncating computer FFT analysis just before the first room reflection arrived. Truncation necessarily attenuates the bass response, so bass must be measured differently. The solution is to move the microphone so close to the cone so that although room reflections do occur during the measurement time, their relative amplitude becomes insignificant(4).
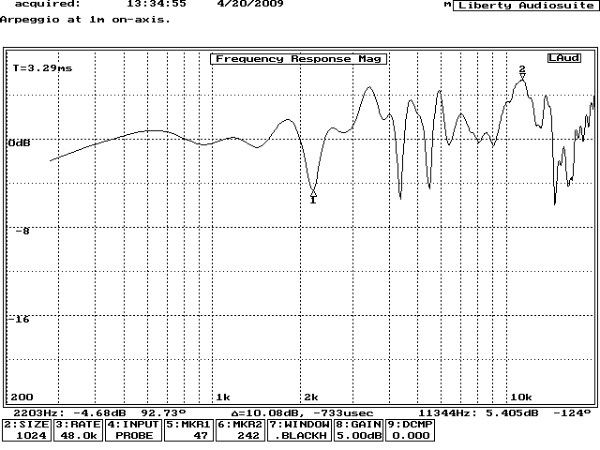
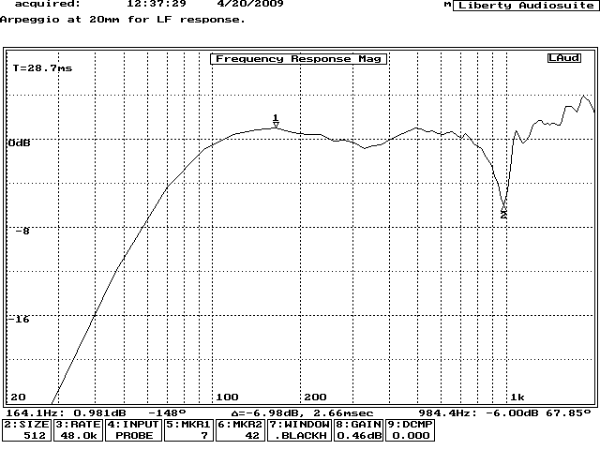
The author is delighted to report that the Arpeggio measures as required when driven from a 6.5 Ohm source resistance. See Fig. 19 and Fig. 20.
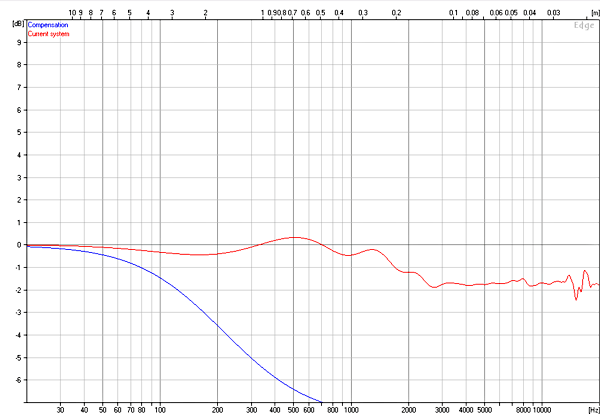
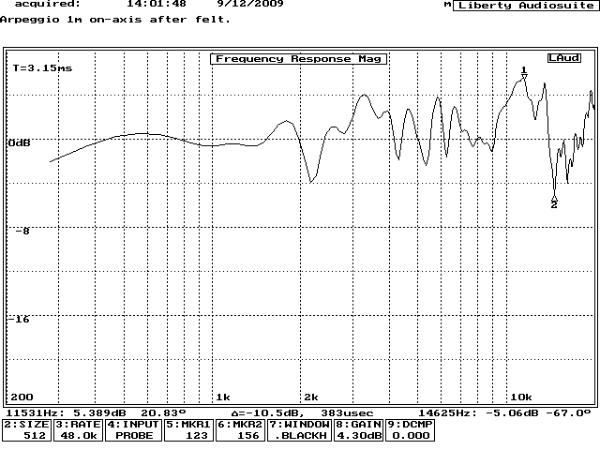
Fig. 19 shows a pleasingly flat response from 500Hz to 2kHz, indicating that aberrations due to baffle diffraction have been minimised, although the 2dB shelf at 2kHz predicted by the “Edge” software did not occur, perhaps due to increasing driver directivity. The flat trend above 2kHz confirms that the Zobel network is operating correctly and preventing the high source impedance from causing a rising response at high frequencies. The abrupt raggedness above 2kHz suggests a mechanical crossover at this frequency to the whizzer cone, nevertheless, the whizzer cone response is surprisingly flat. Note that no smoothing has been applied to “improve” the flatness of this measurement – many loudspeaker measurements are massaged by smoothing or coarse scales.
Fig. 20 shows a flat trend between 100Hz and 600Hz, indicating that baffle step equalisation has been correctly applied. The dip at 984Hz is a measurement artefact due to the obligatory microphone positioning within the cone. The measured bass f-3dB frequency appears to be close to 85Hz, which agrees with the impedance measurement, but is lower than the 93Hz predicted by the Thiele & Small calculation – it is possible that this small but welcome discrepancy is due to wool stuffing increasing the effective box volume but which has not been accounted for in the very simple theoretical model.
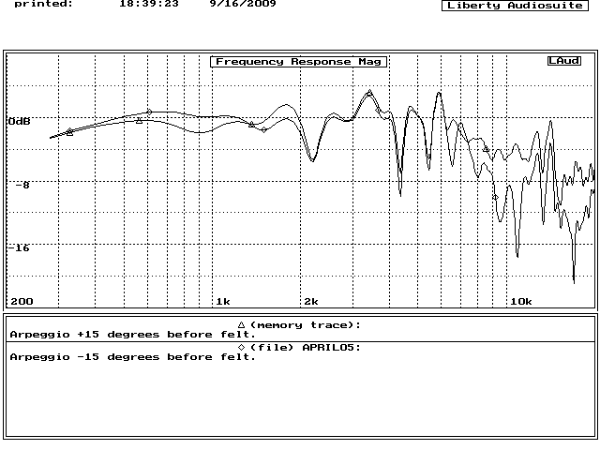
A set of measurements at -30°, -15°, 0°, +15°, +30° was taken before and after felt was added to one of the loudspeakers. There was a slight improvement in the on-axis response, but the clearest indication of the effect of the felt was found by pairing the +15° measurement with the -15° measurement before the addition of felt and repeating this comparison after the addition of felt. Ideally, a comparison between +15° and -15° would produce two exactly overlaid curves because the FE166E loudspeaker is symmetrical, but it is positioned asymmetrically on the box. See Fig. 21.
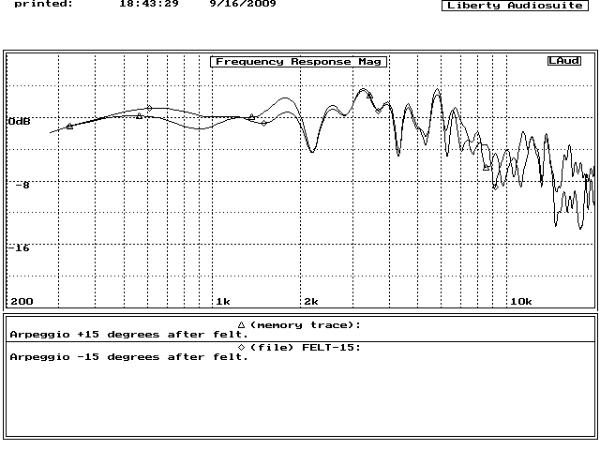
Note that there are two distinct curves with an increasing disparity above 6kHz. Now compare the same measurements after the addition of felt. See Fig. 22.
The disparity above 6kHz has been significantly reduced by the felt.
Returning to the on-axis response, the addition of felt makes the dips at 2.2kHz, 4.3kHz, and 5.3kHz noticeably shallower. See Fig. 23.
Listening
Engineering a loudspeaker with a flat on-axis response is less than half the story. Although it is true that a loudspeaker with a non-flat on-axis response is likely to sound poor, the converse is not necessarily true as it is easy to equalise a poor loudspeaker to give a flat on-axis response.
The author is delighted to report that the Arpeggio sounded good in his 7m x 4m room the instant it received the correct baffle step equalisation. The biggest surprise was the clarity of the bass – this loudspeaker has faults of omission rather than commission. The bass doesn’t go deep but it is very clean and individual notes are easily followed. The next surprise was the clarity and lack of colouration in the midrange, which the author partly attributes to the reduced panel excitation caused by the light cone. The sound of Bach’s Brandenburg Concertos was absolutely super, with convincing strings. (Bach: Brandenburgische Konzerte, Musica Antiqua Köln. Goebel. 1986)
A compromised treble was expected from the dual-cone driver, but it turned out to be perfectly acceptable, although younger ears might be less tolerant (then again, fed on a diet of MP3 players and poor earphones, they might not). With the Arpeggio mounted on a 600mm stand, with the driver at the top, a seated listener is on-axis – this was another reason for choosing the 450mm baffle height dimension. However, dual cone loudspeakers always have poor treble dispersion, so treble falls away rapidly as the listener moves off-axis, but at a listening distance of 4m, positioning is not critical. As expected, the measured response was better above axis than below, and this is why the driver was mounted at the top corner of the box – to provide a good sound to standing listeners.
Deliberately searching for weaknesses exposes the Arpeggio’s lack of bass extension and limited bass power handling.
Bass extension: Albinoni’s “Adagio in G minor for Strings and Organ” became “Adagio in G minor for Strings” – somewhat spoiling the effect. Rock music survived the limited bass extension rather better and the reggae album “Dub Side of the Moon” was surprisingly satisfying.
Bass power handling: The maximum amplifier power that can be applied to this loudspeaker at bass frequencies without excessive cone excursion is ≈ 6W. This limit was determined by listening to a lot of bass-heavy music as loud as was dared whilst simultaneously capturing peak voltages across the loudspeaker using a Tektronix TDS3032 oscilloscope set to infinite envelope mode. Test music included Pink Floyd’s “Dark Side of the Moon” and similar rock from that era (we all listen to the music of our teens). Crude loudness measurements made at the listening distance of 4m using an aged Tandy analogue sound pressure level meter suggested peaks of around 85dBC, but as the meter has a deliberately slow (VU meter) response, true peaks were probably a little higher. Summarising, the Arpeggio excels at voice reproduction and chamber music, but the very articulate bass lacks extension.
Subwoofer
Because the 85Hz roll-off is not peaked, it should be easy to marry a good subwoofer very successfully to the Arpeggio. The ideal crossover would be a 24dB/octave Linkwitz/Riley set to 85Hz using the Arpeggio’s existing 12dB/octave acoustical Butterworth response as one half of the high-pass section. A further advantage would be that filtering the signal would significantly reduce Arpeggio cone excursion, increasing power handling, reducing distortion, and allowing clean 95dB peaks to be easily achieved. However, it would be essential to compensate for the time delay between the subwoofer output and the Arpeggio output to avoid exchanging bass quality for bass quantity. Typically, each 6dB section of a low-pass filter produces delay equivalent to 90° at the f-3dB frequency, so the low-pass section of an 85Hz 24dB/octave crossover is likely to produce a delay of ≈ 12ms. Thus, the high-pass section needs a corresponding delay to avoid transient distortion that is particularly noticeable on snare drums. Even without considering any additional delay contributed by the bass driver, digital compensation seems inevitable.
Probably the most convincing testament to the quality of the Arpeggio is that the author’s LS3/5a have not merely been displaced, but have suffered the ignominy of being carefully packed away in their original cardboard box.
Morgan Jones
Arpeggio Thread for discussion
(1) “Direct-Radiator Loudspeaker System Analysis.” Richard H. Small. Journal of Audio Engineering Society. June 1972. Volume 20. Number 5. pp383-395
(2) “Closed-Box Loudspeaker Systems Part II: Synthesis” Richard H Small. Journal of Audio Engineering Society. January/February 1973. Volume 21. Number 1. pp11-18
(3) “Loudspeaker Enclosure Walls” Peter W Tappan. Journal of Audio Engineering Society. April 1962 .Volume 10. Number 3. pp224-231
(4) “Testing Loudspeakers” 1st Ed. Joseph D’Appolito. Audio Amateur Press (1998) 1-882580-17-6
Last edited by a moderator:
It is always a pleasure to read an article written by an expert, not only in theory, but with hands-on experience.
I will have to adapt the design to construct a new loudspeaker for my 50W push-pull EL43 amplifier - desigend it in 1965, redesigned in 1985, agian in 2003 and still going, either with guitars (separate pre-amps), or turntable.
Skywatch
I will have to adapt the design to construct a new loudspeaker for my 50W push-pull EL43 amplifier - desigend it in 1965, redesigned in 1985, agian in 2003 and still going, either with guitars (separate pre-amps), or turntable.
Skywatch
Symmetry breaking and stiffness - triangular panels
It seems another way to reduce symmetry in the baffle / panel might be be to use a scalene triangular shape.
It has no reflective symmetry unlike rectangular shapes. Plus an added benefit would be increased stiffness compared to a rectangular shape.
One could imagine a "pyramid" or tetrahedron shaped enclosure.
Redhat
It seems another way to reduce symmetry in the baffle / panel might be be to use a scalene triangular shape.
It has no reflective symmetry unlike rectangular shapes. Plus an added benefit would be increased stiffness compared to a rectangular shape.
One could imagine a "pyramid" or tetrahedron shaped enclosure.
Redhat
Bravo Morgan
Morgan - I just received the DiyAudio email newsletter, and was delighted to find your article featured on the webpage, I have had a very quick scan though the pages, and must say I look forward to a more thorough read - great contribution - Cheers, Jack
For more info, Google: Jack Bouska
Morgan - I just received the DiyAudio email newsletter, and was delighted to find your article featured on the webpage, I have had a very quick scan though the pages, and must say I look forward to a more thorough read - great contribution - Cheers, Jack
For more info, Google: Jack Bouska
BRILLIANT article! Excellent explanations.
Everything you say is correct, but some of the effects are too small to worry about.
Instead worry about intermodulation distortion and transients! Steady-state is what builds up in the end - it hardly applies to music!
Box resonances and edge-diffraction: there are two waves - one in the air and others (mainly a bending wave) in the box material. The latter is sped by STIFFNESS and we can make that different in different directions!
The stiffest box I ever made was a dodecahedron: 16 pentagonal tiles - up to 16 speakers; each fills its tile. I would love to see an article on this idea.
Everything you say is correct, but some of the effects are too small to worry about.
Instead worry about intermodulation distortion and transients! Steady-state is what builds up in the end - it hardly applies to music!
Box resonances and edge-diffraction: there are two waves - one in the air and others (mainly a bending wave) in the box material. The latter is sped by STIFFNESS and we can make that different in different directions!
The stiffest box I ever made was a dodecahedron: 16 pentagonal tiles - up to 16 speakers; each fills its tile. I would love to see an article on this idea.
More, please!
Wonderful explanation of all the decisions leading to the final design. It's great to have this in an article - useful as the discussion threads of evolving designs are, it's sometimes hard to sort them out. I hope that other knowledgeable people will contribute articles as Morgan and Nelson have done. Thank you!

bb
Wonderful explanation of all the decisions leading to the final design. It's great to have this in an article - useful as the discussion threads of evolving designs are, it's sometimes hard to sort them out. I hope that other knowledgeable people will contribute articles as Morgan and Nelson have done. Thank you!

bb
Variable impedance amps
Rod Eliot's site has an article on variable impedance amplifiers, mainly how to modify the feedback in a transistor amp to get whatever impedance you need:
Variable Amplifier Impedance
Rod Eliot's site has an article on variable impedance amplifiers, mainly how to modify the feedback in a transistor amp to get whatever impedance you need:
Variable Amplifier Impedance
Different wide range speaker
In my opinion, the Fostex speaker is inferior because it is matching the amplifier power. It should be tested using the 12 inch wide range speaker with above 30Wor more rated power and 99-100dB 1W/1m efficiency. Then you would have neglectable cone movement with big surface and the mass of the speaker magnet and housing would easily compensate for vibrations transfer to the baffle. There are various speakers with these features in the market, for example "Audio Nirvana" etc.
Alltogether, this is the fantastic scientific-engineering approach to show in praxis how it really works. Thanks for all your efforts.
In my opinion, the Fostex speaker is inferior because it is matching the amplifier power. It should be tested using the 12 inch wide range speaker with above 30Wor more rated power and 99-100dB 1W/1m efficiency. Then you would have neglectable cone movement with big surface and the mass of the speaker magnet and housing would easily compensate for vibrations transfer to the baffle. There are various speakers with these features in the market, for example "Audio Nirvana" etc.
Alltogether, this is the fantastic scientific-engineering approach to show in praxis how it really works. Thanks for all your efforts.
Excellent article. I only saw a couple of gaffes. First, the best way to increase the plate resistance of your SET amp is to put an un-bypassed (power) resistor in the cathode circuit. This also lowers distortion. Second, use carbide router bits for your MDF cutting; they last practically forever and are well worth the extra cost.
Very good article, I especially liked the bits about diffraction, driver placement and panel construction, bracing and damping.
Not sure about 93Hz as a cut off though, I think I'd like some bass from a speaker, with a 42 litre vented box you'd get down to 50Hz without any trouble.
I think a lack of any bass at all is often mistaken for lack of woolly bass when people box high Fs drivers into sealed containers.
I have a sealed box that works, but that has a B139 (Fs = 25Hz) and a 72 litre box.
In addition a subwoofer will not be any more precise than a (properly designed without a big bass hump) vented box in my experience.
For stuff without bass however I bet they sound crackingly good, I always like the sound of a whizzer cone driver too for some reason.
Not sure about 93Hz as a cut off though, I think I'd like some bass from a speaker, with a 42 litre vented box you'd get down to 50Hz without any trouble.
I think a lack of any bass at all is often mistaken for lack of woolly bass when people box high Fs drivers into sealed containers.
I have a sealed box that works, but that has a B139 (Fs = 25Hz) and a 72 litre box.
In addition a subwoofer will not be any more precise than a (properly designed without a big bass hump) vented box in my experience.
For stuff without bass however I bet they sound crackingly good, I always like the sound of a whizzer cone driver too for some reason.
a generous contribution from Morgan Jones
Some fine stuff here and generously given to the community, thanks
..a few observations
The 6dB spl diffraction step... is not set in stone, as the power response is maintained...
.....and the step relates to the change, in a free field environment , from spherical radiation at low frequencies to an approximation to 2pi baffle radiation at higher frequencies.
A listening room is not free field and so returns a fair measure of the off and rear radiation at low frequencies back to the listener as both pressure and reverberation, depending on frequency. Typically the step correction need only be 3dB and one may adjust to taste and local acoustic.
I agree with that contributor, that if you can afford it marine grade Baltic or Russian ply is a fine panel choice over MDF which is a bit hard sounding and characterless, but I am nitpicking here.
Bracing is a complex matter as you need to know the shape of the resonant panel modes and then brace according to amplitude and how that mode shape is radiated .
Ironically a brace can reshape a mode so that it is louder due to increased radiation efficiency.
Concerning the Zobel this is a nice touch to maintain the match to a 6.5ohm source.
May I suggest that the magnet is a magnetically and vibrationally noisy location, and that film capacitors are surprisingly microphonic. It would be worth trying them in a quite place eg at the terminals and not on the driver.
Even for a sealed box such as this I would favour rolling up the stuffing and tying it down in a relatively central location. Builders can also tweak the Zobel values to act as a tone control.
The reason the 4'5 ohm resistor addition is possible for a lower output, high Z amplifier is that valve- tube amps happily increase their voltage swing in to higher impedances. So a 10W output into 4 ohms may well swing a 10W equivalent drive voltage into 8ohms; the load line simply rematches.
Even quite high NFB tube amps behave this way.
Some heavy work on RFI reported in the latest issue of HIFICRITIC has confirmed the radio aerial properties of the loudspeaker and its connecting cable.
Some improved results have been reported with 10n 250 V or higher (high quality pp film , even Mundorfs have been used) in series with 76 to 160 ohm ( try them out) wired as a high frequency Zobel across the speaker terminals.
Commercial devices of this type can cost $200 a pair !
The purpose is to gently snub the RF in the speaker and wiring where the cables etc are typically 50 -150 impedance at RF , eg above 1MHz. bigger caps don't seem to work, you need to consider their self resonance frequency.
This RF gets in the amp and for many types we have tried at HIFICRITIC , subtly adds grain and reduces transparency.
RFI is a big issue and as we begin to try and control it , source to load , all cables including mains, and up from the supply , we are finding it a much greater factor in high fidelity than we expected.
Martin Colloms
Tech Ed HIFICRITIC
HIFICRITIC, audio review magazine, hi fi critic
Some fine stuff here and generously given to the community, thanks
..a few observations
The 6dB spl diffraction step... is not set in stone, as the power response is maintained...
.....and the step relates to the change, in a free field environment , from spherical radiation at low frequencies to an approximation to 2pi baffle radiation at higher frequencies.
A listening room is not free field and so returns a fair measure of the off and rear radiation at low frequencies back to the listener as both pressure and reverberation, depending on frequency. Typically the step correction need only be 3dB and one may adjust to taste and local acoustic.
I agree with that contributor, that if you can afford it marine grade Baltic or Russian ply is a fine panel choice over MDF which is a bit hard sounding and characterless, but I am nitpicking here.
Bracing is a complex matter as you need to know the shape of the resonant panel modes and then brace according to amplitude and how that mode shape is radiated .
Ironically a brace can reshape a mode so that it is louder due to increased radiation efficiency.
Concerning the Zobel this is a nice touch to maintain the match to a 6.5ohm source.
May I suggest that the magnet is a magnetically and vibrationally noisy location, and that film capacitors are surprisingly microphonic. It would be worth trying them in a quite place eg at the terminals and not on the driver.
Even for a sealed box such as this I would favour rolling up the stuffing and tying it down in a relatively central location. Builders can also tweak the Zobel values to act as a tone control.
The reason the 4'5 ohm resistor addition is possible for a lower output, high Z amplifier is that valve- tube amps happily increase their voltage swing in to higher impedances. So a 10W output into 4 ohms may well swing a 10W equivalent drive voltage into 8ohms; the load line simply rematches.
Even quite high NFB tube amps behave this way.
Some heavy work on RFI reported in the latest issue of HIFICRITIC has confirmed the radio aerial properties of the loudspeaker and its connecting cable.
Some improved results have been reported with 10n 250 V or higher (high quality pp film , even Mundorfs have been used) in series with 76 to 160 ohm ( try them out) wired as a high frequency Zobel across the speaker terminals.
Commercial devices of this type can cost $200 a pair !
The purpose is to gently snub the RF in the speaker and wiring where the cables etc are typically 50 -150 impedance at RF , eg above 1MHz. bigger caps don't seem to work, you need to consider their self resonance frequency.
This RF gets in the amp and for many types we have tried at HIFICRITIC , subtly adds grain and reduces transparency.
RFI is a big issue and as we begin to try and control it , source to load , all cables including mains, and up from the supply , we are finding it a much greater factor in high fidelity than we expected.
Martin Colloms
Tech Ed HIFICRITIC
HIFICRITIC, audio review magazine, hi fi critic
First, a "Thank you" to Martin Colloms for his observations. As he's the author of "High Performance Loudspeakers" (now into its 6th edition, and thoroughly recommended), we can assume he knows of what he speaks. His comment about baffle step and 3dB is spot-on, since I only needed 2.4dB in my living room. As for positioning braces, I'm ready to believe that there could be better or worse positions, but the central position seems to work and gives the baffle around the drive unit support. I agree that capacitors can be microphonic, but my reasoning for glueing the capacitors to the magnet was that it has a lot of mass and is rigid - which is probably more than can be said for anywhere else in the box! Still, it's an easy enough change to experiment with.
I think the stuffing observation is valuable and well worthy of experimentation. The one thing we do not want is to shake the mass of stuffing up and down. I would expect changes here to affect the bass and low midrange.
I did initially do some calculations on the palliative effect of the flatter loadline allowing greater voltage swing into the loudspeaker plus series resistor, and therefore restoring some of the power you'd expect to lose, but the effect wasn't as great as I'd hoped and the article was already getting quite long, so I left it out.
RFI is insidious - especially if you consider loudspeaker cables to be aerials connected to an amplifier's input stage via a global feedback loop. I seem to remember A N Thiele writing an AES article about this effect and suggesting RF filters at the output of the amplifier. The RF Zobel idea seems to be more aimed towards preventing the loudspeaker cable acting as an incorrectly terminated (and therefore resonant) transmission line.
I think the stuffing observation is valuable and well worthy of experimentation. The one thing we do not want is to shake the mass of stuffing up and down. I would expect changes here to affect the bass and low midrange.
I did initially do some calculations on the palliative effect of the flatter loadline allowing greater voltage swing into the loudspeaker plus series resistor, and therefore restoring some of the power you'd expect to lose, but the effect wasn't as great as I'd hoped and the article was already getting quite long, so I left it out.
RFI is insidious - especially if you consider loudspeaker cables to be aerials connected to an amplifier's input stage via a global feedback loop. I seem to remember A N Thiele writing an AES article about this effect and suggesting RF filters at the output of the amplifier. The RF Zobel idea seems to be more aimed towards preventing the loudspeaker cable acting as an incorrectly terminated (and therefore resonant) transmission line.
Hi Morgan
This project reminds me of an experience I had circa 1975 or 1976 here in Sydney. Allen Wright showed me this Jap 6" fullrange drivers and I went to the importer to get a pair. The brand is no longer available, it was Foster, I believe same as Fostex. As I was paying for them I was told that I ought to get in touch with a chap at Sydney University who had measured these drivers and who might be helpful to me. I did phone him and he promised to send me some computer print-outs. I was shocked that they argued for the addition of series resistance (resistors) to overcome too damped alignments when put into various box volumes as per a computer print-out-table. I then got back to him and started to blurt out about the effect this would have on damping factor blah blah blah. He would have none of it - it was the alignment that mattered and clearly damping factor was no issue with him at all - it was the alignment that mattered, period! Took me a long time and a lot of thinking and finally realised he was right. The gentleman's name? Richard H. Small. Yes, I was arguing against the one and only Mr. Small - what a silly dill I was.
Cheers, Joe Rasmussen - BTW, still getting to ETF regularly? Like to get back there next year.
This project reminds me of an experience I had circa 1975 or 1976 here in Sydney. Allen Wright showed me this Jap 6" fullrange drivers and I went to the importer to get a pair. The brand is no longer available, it was Foster, I believe same as Fostex. As I was paying for them I was told that I ought to get in touch with a chap at Sydney University who had measured these drivers and who might be helpful to me. I did phone him and he promised to send me some computer print-outs. I was shocked that they argued for the addition of series resistance (resistors) to overcome too damped alignments when put into various box volumes as per a computer print-out-table. I then got back to him and started to blurt out about the effect this would have on damping factor blah blah blah. He would have none of it - it was the alignment that mattered and clearly damping factor was no issue with him at all - it was the alignment that mattered, period! Took me a long time and a lot of thinking and finally realised he was right. The gentleman's name? Richard H. Small. Yes, I was arguing against the one and only Mr. Small - what a silly dill I was.
Cheers, Joe Rasmussen - BTW, still getting to ETF regularly? Like to get back there next year.
- Home
- General Interest
- diyAudio.com Articles
- Arpeggio Loudspeaker