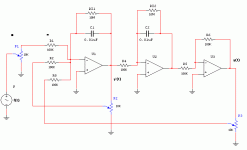
Here is a circuit that represents a forced, damped, harmonic oscillator. It is a differential equation of the form:
a y'' + b y' + c y + f(x) = 0
Assume the initial conditions are y' = y = 0. My question is this: How do I express a, b, and c, from the above equation, in terms of p1, p2, p3, r1, r2, c1, c2, etc? Assuming p1,p2 are attenuation factors in the range [0,1].
a y'' + b y' + c y + f(x) = 0
Assume the initial conditions are y' = y = 0. My question is this: How do I express a, b, and c, from the above equation, in terms of p1, p2, p3, r1, r2, c1, c2, etc? Assuming p1,p2 are attenuation factors in the range [0,1].
Attachments
Hmmm... It occurs to me that this might be in the wrong forum... regardless, I would really like some help with this problem..
Here is what I have so far:
the diffential equation can be re-written as
y'' = -1/a [ by' + cy + f(t) ]
y = -1/a Integral[ by' + cy + f(t) ]dt
and the voltage on the output of the first (summing) integrator is
Vout = y'(t) = -1/(c1) Integral[V1/R1+V2/R2+V3/R3 ]dt
where V1..V3 are the voltges before R1..R3. If we include the attenuation factor of the three pots, we get:
Vout = y'(t) = -1/(c1) Integral[f(t)*p1/R1+y(t)*p3/R2+y'(t)*p3/R3 ]dt
comparing with the above equation, this would lead me to believe that
a = c1, b=p3/R3, c=p3/R2
the only thing is, this doesnt take into account the second integrator....
any ideas??
Here is what I have so far:
the diffential equation can be re-written as
y'' = -1/a [ by' + cy + f(t) ]
y = -1/a Integral[ by' + cy + f(t) ]dt
and the voltage on the output of the first (summing) integrator is
Vout = y'(t) = -1/(c1) Integral[V1/R1+V2/R2+V3/R3 ]dt
where V1..V3 are the voltges before R1..R3. If we include the attenuation factor of the three pots, we get:
Vout = y'(t) = -1/(c1) Integral[f(t)*p1/R1+y(t)*p3/R2+y'(t)*p3/R3 ]dt
comparing with the above equation, this would lead me to believe that
a = c1, b=p3/R3, c=p3/R2
the only thing is, this doesnt take into account the second integrator....
any ideas??
- Status
- Not open for further replies.