Hi all,
As you know, there is a lot of 24bit DACS today. But my thinking is along these lines,
Only with 24bit source material are these of any use (and even then bits nearer the tops aren't real electrical bits, which I believe why multi-bit is more popular).
I think up conversion from 16bit to 24bit modulators can hurt the sound and that it's better to play 16bit material via a 16bit or less device (14bit 1540 anyone?)
So what of the 8bit multibit section of the all-so-common delta-sigma dac of today? can this be exploited?
Because if you have access to software which you can vouch as fixed point throughout, and then down convert all 16bit material to 8bit (edit: properly dithered but lets not discuss dither!) and pass this down-converted data through kernel-sound interface on windows, being confident and certain the data is 8 bit, then technically speaking, if the sound device is a DS modulator (most common and typically multibit upto 8bit or so, before the oversampling section takes over) then in essence you are utilizing the whole fully electrical current divider section of the DAC only to generate the sound.
After alot of tracking down I found software which down convert to 8bit in fixed point.
I'm confident it is fixed point because as you lower the software's volume control, the quantization distortion worsens as the level is reduced - this is tell tale sign not found in other players. At full volume however the sound is fine.
So to refresh, I think there is way too much ambiguity with how software/hardware interfaces is handles data today, for instance, a lot of software is floating point, which I presume up-converts to it's native IEEE '24bit', onto which the sound card, upon reception interprets and applies best filters/routines to play the material. A dubious process.
In all I think we'd all agree its best practice to start with as much precision at ADC side as possible and play through a same or lesser precision device but not the other way around, i.e. 16bit through a 20bit DAC, as more question arises about how this process is handled. (where as vice versa, its plain truncation).
What is the forums opinion ?
P.s. The software I found is XMPlay (free and light at 369kb). There is an 8bit option in there.
Seperately, I find 8-bit synthesizers sound the most natural, providing done right regarding filtering...
As you know, there is a lot of 24bit DACS today. But my thinking is along these lines,
Only with 24bit source material are these of any use (and even then bits nearer the tops aren't real electrical bits, which I believe why multi-bit is more popular).
I think up conversion from 16bit to 24bit modulators can hurt the sound and that it's better to play 16bit material via a 16bit or less device (14bit 1540 anyone?)
So what of the 8bit multibit section of the all-so-common delta-sigma dac of today? can this be exploited?
Because if you have access to software which you can vouch as fixed point throughout, and then down convert all 16bit material to 8bit (edit: properly dithered but lets not discuss dither!) and pass this down-converted data through kernel-sound interface on windows, being confident and certain the data is 8 bit, then technically speaking, if the sound device is a DS modulator (most common and typically multibit upto 8bit or so, before the oversampling section takes over) then in essence you are utilizing the whole fully electrical current divider section of the DAC only to generate the sound.
After alot of tracking down I found software which down convert to 8bit in fixed point.
I'm confident it is fixed point because as you lower the software's volume control, the quantization distortion worsens as the level is reduced - this is tell tale sign not found in other players. At full volume however the sound is fine.
So to refresh, I think there is way too much ambiguity with how software/hardware interfaces is handles data today, for instance, a lot of software is floating point, which I presume up-converts to it's native IEEE '24bit', onto which the sound card, upon reception interprets and applies best filters/routines to play the material. A dubious process.
In all I think we'd all agree its best practice to start with as much precision at ADC side as possible and play through a same or lesser precision device but not the other way around, i.e. 16bit through a 20bit DAC, as more question arises about how this process is handled. (where as vice versa, its plain truncation).
What is the forums opinion ?
P.s. The software I found is XMPlay (free and light at 369kb). There is an 8bit option in there.
Seperately, I find 8-bit synthesizers sound the most natural, providing done right regarding filtering...
Last edited:
Way too many unfounded assumptions, not to mention not understanding basic physics and math. You put your won foot in your mouth - this means that we could have long solved the 'problem' of proper CD playback by 'simply' losing bits of precision forever and playing thorugh less precise DACs. If so, why stop at 8 bits? Whan CD was designed, you could buy 8-bit DACs for subdollar prices already, yet literally hundreds of thousands of man-hours were invested into developing precise higher bit ones from then, to now, with lots of new knowledge and understanding - and the sound did not get worse, but better.
PS, have you ever wondered what makes an 8-bit synth sound right IF it's filters are done right? And why is it specifically the filters?
PS, have you ever wondered what makes an 8-bit synth sound right IF it's filters are done right? And why is it specifically the filters?
Marketing pedaling of increasingly better specs of the ever higher bit converters kept the bits rolling, dunno, something to highlight, to out-do competition and sell. If the industry was given the opportunity to hear the difference in noise between 8 and 16bit systems at moderate, normal listening levels with perhaps a graph to comparing typical noise of a reel to reel beside an 8 bit system, more informed decisions would have been made and 20bit would probably would be considered the max required and seen advertised today. Dubiousness arises I think because 24bit is useful for preservation during transmission and number crunching internally, after conversion and because digital is complicated of course.
They must be time-continuous. Dave Rossum, among other designers of the first digital systems who at the time had a fresh perspective and background in analog electronics, was careful enough to ensure his 8bitter synths where non-linear-phase (intra-channel), which imo is considered more benign in audio, considering the non linearity of all the other mediums being used at the time, including the human ear itself, but linear-phase still somehow found a home in the highly mathematically and carefully contrived digital audio, pedaled by lack of understanding, partially on the consumers part, who in the end just trust to get the best if they spend enough.
Back to what I asked initially though, I feel the soundcard that is, beyond operating system, sound layers, APIs etc etc what have you, should receive data clear, without software interfering(!)
A non audio related example of this software issue; when I use the latest software and the latest codec on a crummy old 1.8ghz single core from 2005, to play 1080p video, it's slow as heck. I blame bloated software in general, in contrary when I use the corecodec H.264 directshow filter in conjunction with windows media player 8 from 2003, 1920x1080 MP4 works FINE, on the same 'slow' 1.8ghz, 1gb ram machine, a smooth as a jag without problems.
Hardware / Software. If hardware isn't done right it doesn't work, period. Software and code is more versatile, and is more of a bane. But this is besides the topic, i'm just using it as an example to prove that as time goes on there is more and more discontinuities in practices because everybody is too concerned with 'doing it their way', not necessarily a bad thing but there is too much ambiguity in software today period (forget about plugins, lets not go there). Phew.
Same applies to web browsers, some sites work flawlessly lightening speed on 'outdated' java and flash but some require the latest latest latest chrome or whatever just run, and badly at that, even on a 4ghz quad core machines! Why does firefox need 200mb aside for plugin? bloatware that's why.
Do try that XMPlay in 8bit mode though, just to experience how appealingly bad 8 bit is (not).
Last edited:
Music production =/= music reproduction.
Bit depth sets the noise floor- it's not that important for a synth, but a hissy background during quiet passages of a recording can be annoying. As soon as you say something like "let's not discuss dither," you're already running down the wrong path for music reproduction.
Bit depth sets the noise floor- it's not that important for a synth, but a hissy background during quiet passages of a recording can be annoying. As soon as you say something like "let's not discuss dither," you're already running down the wrong path for music reproduction.
I should have written 'providing optimal dither schemes is employed' which is what I implied by that saying don't mention it i.e. ignore it, assuming everyone on here would understand it and that.
To clarify what I'm stabbing at, 24bit DAC playing 16bit file is less optimal than a 16 or 14bit DAC playing a 16bit file. This is my case. I don't think there is anything horrific about 8bit, (providing optimal d-word is used - heck even without that, 8 bit doesn't sound too objectionable in the first place, ok it's not greatest but what about 12bit which IS on par with reel to reel).
Every sound device must detect input format then set appropriate filter and I feel this is the bit that is highly ambiguous today...
It's more comfortable sitting with a 16bit device knowing it plays what it receives, without anything dubious going on in between. Is My Point.
Every sound device must detect input format then set appropriate filter and I feel this is the bit that is highly ambiguous today...
It's more comfortable sitting with a 16bit device knowing it plays what it receives, without anything dubious going on in between. Is My Point.
Last edited:
Nothing particularly dubious going on or so it seems to me.
If I have a 16 bit input and a 24 bit DAC core I just stuff the 16 bits into the 16 MSB slots (and handle the sign extension correctly), no magic, just engineering, but now if I turn down in software I have maybe 4 bits or so above the system noise floor to attenuate into before I hit the noise floor, with a 16 bit DAC I do not have that because my dither noise must always be around 1 LSB....
The lions share of the audio production world is floating point, because there the extra headroom is sometimes important (And floating point is in some ways easier to write then fixed point), not much point in sweating it on the playback side given the nature of the tools the production folks use (Protools was fixed point for a while mainly down to the historical need to offload onto DSP cards, and what was available at the time).
BTW you have an overly simplistic view of both hardware and software, either can be screwed up in more or less subtle ways, (For example there was a popular 8 track recorder that in one of its iterations get the LRClk phase wrong so there was a permanent 1 sample offset between odd and even outputs, **** happens.
Regards, Dan.
If I have a 16 bit input and a 24 bit DAC core I just stuff the 16 bits into the 16 MSB slots (and handle the sign extension correctly), no magic, just engineering, but now if I turn down in software I have maybe 4 bits or so above the system noise floor to attenuate into before I hit the noise floor, with a 16 bit DAC I do not have that because my dither noise must always be around 1 LSB....
The lions share of the audio production world is floating point, because there the extra headroom is sometimes important (And floating point is in some ways easier to write then fixed point), not much point in sweating it on the playback side given the nature of the tools the production folks use (Protools was fixed point for a while mainly down to the historical need to offload onto DSP cards, and what was available at the time).
BTW you have an overly simplistic view of both hardware and software, either can be screwed up in more or less subtle ways, (For example there was a popular 8 track recorder that in one of its iterations get the LRClk phase wrong so there was a permanent 1 sample offset between odd and even outputs, **** happens.
Regards, Dan.
OK, since you called out to have your post dissected, here goes.
Quotation, explanation, proof??? Just a lot of 'thinking' and 'opinion' based on very little actual data and knowledge.
All PCM samples are normalized to +-1.0, which means they contain the N MOST SIGNIFICANT bits of an 'infinite' resolution binary number, N being the number of bits in a sample minus 1 (the most significant bit is used as a sign). In other words, extending a 16 bit sample to 24 bits involves all of adding 8 zeros at the end, producing the exact same binary number. How did that hurt resolution? This is basic binary math.
However, to be a 16 bit converter, the bits have to be accurate to at least one more bit past the 16th bit, i.e. to at least half of the 16th bit or better. A 24 bit converter, theoretically, has to be accurate to half of the 24th bit, 256 times more accurate than a 16 bit converter when reproducing 16 bit samples. Again, how does this hurt things???
In the real world, actual 24 bit accuracy while maintaining the standard 2V RMS output is a near physical impossibility, so the BOTTOM and NOT the top bits (so you are dead wrong here and would know it if you had any notion of the most basic binary math, as in which bit carries which weight) in a 24 bit converter are not real because the actual resolution is more like 20-21 bits. That being said, that kind of converter is still 16-32 times more accurate in reproducing 16 bit samples than a 16 bit one, so again, how does this hurt 16 bit reproduction???
There is no such thing as a 16 to 24 bit 'modulator'. There is a 16 to 24 bit FILTER, for example an oversampling filter, which is not used if you only want to extend the bit depth at the same sample rate.
The reason for this is that filter coefficients are fractional numbers which, even for a filter operating on 16-bit input data, may not be accurately represented in 16, or for that matter 24, or for that matter infinite number of bits (like 1/3 cannot be represented in a finite number of decimal places). Digital filtering is a series of multiply-add operation on a first-in first-out buffer, and if one wants to keep thing accurate, it has to work with a lot more precision than the input data, in fact just reducing the coefficients to 16 bits may produce a worse filter and loss of precision on the output, so 40 or more bits was not uncommon even 25 years ago, while now 56 or 64 is the standard. Because 16 bit precise data multiplied by eg. 24 bit precise coefficients can generate results with more precision than 16 bits, the first filters had to reduce bit depth back to 16 bits at the output and of course apply proper dithering while doing it, in order to convert this data into analog using a 16 bit converter. As a result, a 16 bit DAC driven by a digital filter, driven by 16 bit samples, will lose about half a bit of precision. Soon after this first generation two methods were applied to counter this, which are using a more than 16 bit (18, 20 bit) ADC, and noise shaped dither, which pushed the loss of resolution into an ultrasonic region that the output filter after the DAC would almost completely remove, therefore preserving the maximum of the 16 bits of the data.
And while you are mentioning the venerable 1540, it was driven at a 4x rate with a noise shaped digital filter (one of the very first ones!) to actually attain virtually 16 bit resolution – because that's what proper noise shaped dithering can do, as long as there is extra bandwidth to push the noise into.
The current SD modulator based DACs do exactly the same thing, the difference is in the way the DAC attains high bit resolution, and in some cases this can open up more space for better dithering and noise shaping.
What about it? It is not a 8 bit PCM DAC nor is it accessible in any way except perhaps in DSD mode if the chip actually supports DSD data bypass, but then it only uses one bit input. It is usually a potentiometric DAC, which for N bits has N+1 states. Typically it's 6 to 8 bits and therefore has 7 to 9 states, around 3 bit resolution. It always has N=A bits 1 + B bits 0. The trick is that, for instance if 3 bits are on and 5 off, it randomly choses a different set of 3 bits out of the 8 available to be 1, for every sample where 3 bits are on and 5 off. What this does is statistically averages out the tolerances in the actual 8 bits – which should all be exactly equal, but since this is the real world, they are subject to tolerances.
More advanced chips actually use real 6 bit encoding and drive a 63-bit potentiometric DAC, to have even more bit elements to average out the imprecisions. This method of operation is commonly known as dynamic element matching. Why this high precision in a low bit DAC? This is because SD DACs trade amplitude precision for time precision by reducing the number of bits and driving them very fast with a bunch of noise shaping, BUT the actual bits still need to be very precise. This is because in theory to get each extra bit of resolution you need to increase the speed by a factor of two, without noise shaping. With noise shaping the factor drops down but faster than the requirement for precision for the actual real bits without noise shaping. Still, it is obviously much easier to get say 20 bit precision in 6 bits than in 20 bits! For instance using a 63 element potentiometric DAC to get 6 real bits of resolution will reduce the tolerance of a single element by a factor of around 5.6 (this is equal to about 2.5 bits more precision than a regular say R2R 6-bit DAC using the same elements).
If you had access to this DAC you would have to use it exactly as it is already been used to get the same result, everything else will be WORSE not better.
Completely wrong. Oversampling is done FIRST in order to get to a sample frequency which gives you enough space above the audio band to push enough of the quantization noise into the unused part by noise shaping as you next do bit depth reduction. Doig otherwise would result in loss of resolution right from the start and would be clearly audible and visible in measurements.
Some additional oversampling may occur without noise shaping and dithering at the highest sampling rate stages to implement more advanced dynamic element matching.
Weather the software is fixed point throughout has no relevance here. You can't get better than the actual resolution of a DAC chip at it's highest sampling rate by reducing the bit depth, period. Once you have reduced the bit depth, data is lost – the only question is how much and in what frequency range, and how it is decorrelated in order for it not to cause large losses in narrow bands but rather smaller losses smeared across wider bands (i.e. the loss has to convert to noise, not distortion and intermodulation). If your DAC is N bit accurate at your sampling rate and bit depth, regardless of how it got to that resolution, you can't get better than that by any noise shaping you can do externally overall. You may get a slightly better trade-off if you can apply more sophisticated noise shaping than the DAC itself between in band and out of band noise, assuming you can circumvent the built-in digital filters or trick them by concurrently upsampling the incoming material, or the incoming material is already 'content empty' in high frequency.
Which brings me to the astonishing amount of people who think they understand digital audio, and have no notion of noise shaping and dithering, would not recognize it looking directly at it. Many such a guru keeps showing us on youtube how it's hardly possible to hear any difference between 16 and 24 bit samples - while this might be true, the demos are downright wrong if not misleading.
One of them does so while wearing a wool hat over half an inch of hair covering his ears. He proceeds to demonstrate his thesis by reducing the bit depth in a well known audio processing program, keeping the sampling rate high. Then he says he can't hear a difference, but that there is one when looking at the file using a spectrogram view. And shows it to us as 'some sort of strange noise rising in frequency outside of the audio band'. Fortunately, his program is much more clever than he is and knowing it's stuff, applied proper noise shaped dither in an attempt to keep as much of the extra bits of resolution over the target 16 of the file in the audio band, so the typical noise shaping noise vs frequency distribution is nicely visible. He then proceeds to 'explain' this 'phenomenon' with 'I think' followed by sentences which have no base in reality, and must be so just because he 'thinks it'. I will remind readers that 'I think' means using the brain to think about the possible causes and evidence, and not using it to merely believe. Also, when doing such a demo use a file that actually has more than 6 bits of dynamic range, which you will actually notice if you make a path to your ears past the hair and woolen cap.
Again, completely wrong assumptions based on more assumptions as explained in the next to bottom paragraph.
How do you think 'other players' magically avoid quantization distortion? It's not like it's magic, it's just plain dithering. The difference is, with say 16 bits of resolution you can actually reduce volume to a point where you still cannot hear the distortion because you still have spare bits and with 8 bits you run out at -50dB or so, which is still clearly audible given a reasonably quiet ambient. With 16 bits, you still have 40dB or so to spare at -50dB volume, more than the instantaneous dynamics of a (really good!) human ear.
At full volume the sound is fine because the noise is some 50dB below, which is more than the instantaneous dymanic range of the human ear, and therefore imperceptible at that level unless in a completely different band.
Which brings me to the matter of dynamics and number of bits per sample. As SY eloquently said, sound reproduction is NOT sound recording. No-one needs real 24 bits of dynamic range while recording because no-one records in an underground anechoic chamber.
Let me use an example: 144 dB of dynamic range is letting you accommodate to the lack of sound in an anechoic isolation chamber to the point where you can hear your own bloodflow, and then firing a handgun 1 meter away from you. It can be done only once because it WILL result in hearing damage. Immagine getting that dynamic range with a very quiet (30dB background noise) recording venue – now the baseline is 30dB and the loudest noise would have to be 144dB over that – 174dB. At this loudness the recording session would last for about 1 second because everyone would be deaf after that, and this would surely make it difficult to continue, if the involontary spasming of your eye muscles due to your eyes and lungs vibrating to the noise would not. Yes, there are instruments that can generate astonishingly high sound pressures in peaks (120-130dB! and not good for the player of that instrument) but they last very short and this is measured to the absolute 0dB level, so relative to a quiet 30dB recording venue, this is 90-100dB – and 30dB is a VERY quiet recording venue.
Still, even if faithfully recorded, this sort of recording would be lost on the human ear in reproduction – even young and female ears are capable of at best 40-50dB instantaneous dynamics. In other words, if there is a loud peak, for a while later (in seconds) you will be completely deaf for anything 40-50dB quieter, while the ear adjusts again. It reacts much faster to attacks than to decays, and in reality you are lucky if you can manage 30dB of instantaneous dynamics.
In other words, 24 bits are there to accommodate various relative levels needed in mixing the various recorded channels, plus processing. Nowadays the most convenient format is 32-bit fixed point, which is used for processing usually by extending the range by some bits on the most significant end, depending on the number of channels on the mixer (16 channels, 4 bits – because a full scale input on all channels will generate a 16x larger output worst case, for which 4 bits are needed to prevent clipping). The rest of the bits are used as a 'gutter' for accruing errors due to processing with a finite resolution. Once the mix is done, everything is normalized back to +-1 (MSB aligned) and the final reduction in bit depth is done if needed (which of course includes proper noise shaped dithering).
Arguably, real reproduction circumstances make anything over 16 bits superfluous, though it could also be argued that extra bandwidth (higher sampling rate) is beneficial to a degree – however with proper noise shaped dither applied, the requirements are not as great as one would imagine, 24/96 is already overkill. The reason is found in the normalized curves for the sensitivity of the human ear (1 of them) vs frequency. Even so, some extra bandwidth is good because the human hearing is based on earS (2 of them) being able to discern differences in phase and delay smaller than the raw bandwidth of a single ear would suggest. This would lead us to discussions about DSD but that is outside the scope here.
The point is, while more than 16 bits of bit depth may be overkill, in today's world of abundant storage and 64-bit wide CPUs the most convenient data width that is over 16 bits is 32, and the amount of data on a 1 hour CD is considered 'not so bad' so 32-bit and higher sampling rates are here to stay even as a transport format, though it's largely empty or noise-filled.
And an even more dubious assumption. Yes, some software will apply all sorts of mediocre signal processing without telling you, but which software does not or the processing is avoidable, is fairly common knowledge.
Software is often 32-bit floating point which is technically a complete bodge of a 'solution', given that it requires repacking of data (and associated time lost) and provides 24 bit resolution WITHOUT any real data protection from overflows or rounding error creepage. In fact, both of these phenomena will result in loss of precision. While the floating point number range is huge, the precision of each number is only 23 binary digits plus sign – just like the native 24-bit PCM. 32-bit integer would have been a better choice. However, when DSP-like instructions were added to the Intel CPU instruction set, in form of MMX/3Dnow instructions (and later derivatives), they could only be added to the floating point unit while retaining compatibility. So, today, 18 years later we are still victims of that decision, fortunately most serious programs will now use double precision float and get about 48 bits of resolution.
If your program uses 32-bit float, you better disable all processing if you want to retain 24 bit resolution (as to how much it matters, see above paragraph).
The initial assumption is dubious because 32-bit or for that matter any bit floating point is NOT native to any audio DAC. Neither does the 'audio card' apply any filters or interprets anything to apply any filters, this is entirely driven by how the DAC on the audio card is implemented and what options were selected for it's integration onto the card.
This brings us to the 'problem' of higher sampling rates. This primarily has to do with the requirement for brick wall filtering if you want your ADC to produce standard PCM encoding, and your DAC to convert it to analog. The initial 44.1 CD format left a very narrow 2.05kHz range (and assumed a 20kHz bandwidth) into which one had to squeeze a filter that drops the signal 96dB – the equivalent of a 159th order filter expressed in classical analog terms. This is not a trivial matter to implement even with digital filtering and get anything approaching good time domain response. In the analog domain it is close to impossible and doubly more so because you need two exactly equal ones, one for each channel. Doubling the sampling rate to 88.1k increases this transition range to a comparatively massive 46.15kHz – a 22.5 fold increase, severely relaxing the requirements for the filter – even while increasing the usable bandwidth. Even more so with further increases to 96k, 176.4 or 192k – all well known from the olden days of 4x oversampling. Because you actually WANT to increase the bandwidth and not oversample an existing low sampling rate signal, you do not need a brick wall filter at the ADC nor the DAC – a much less severe one is needed and this can be designed for excellent time domain response far above what anyone is able to hear.
It should be noted that the time response you can get is defined ultimately by the sampling rate, not the bit depth. Because of this, DSD is many times more accurate in the time domain than even the highest used PCM – but this comes at a trade-off in resolution in order to keep the amount of data in reasonable limits, and it assumes it was not derived from a PCM master.
In most cases the filtering chosen inside the DAC – and these days all DACs have it built in (and be thankful for that because the people that had to build those first brick wall filters in the analog domain would probably strangle you given the same task again instead of implementing it digitally) – is done based on the sample rate, since it is assumed that the first 20k of the available bandwidth are of most interest. Digital filters scale with sampling rate but the absence of need for a brick wall filter for higher sample rates has made most manufacturers provide more relaxed and time domain accurate filters for sampling rates above 64k.
Now, if a sound card chooses to apply extra processing, this is it's own fault – however, in most cases a serious PC audio system does not use a sound card but rather some sort of data bridge to convert a stream as read from a file to either SPDIF or I2S in the end, possibly using other transport methods on the way (such as USB). All of these have their own problems, none of which have to do with the actual DA conversion – though the quality of the DAC output can be impaired along the 'garbage-in = garbage-out' principle.
Again, completely wrong – the process of extending bit depth is 'plain' and trivial with no loss (you would have to be truly amazingly incompetent to get it wrong) while reducing bit depth is DEFINITELY NOT just 'plain truncation'. Plain truncation is exactly what makes it sound bad, which is why dithering is needed in the first place.
So what kind of an opinion should one have of ideas which are based on assumptions where every single assumption is wrong? See above under 'garbage in = garbage out' principle.
Quotation, explanation, proof??? Just a lot of 'thinking' and 'opinion' based on very little actual data and knowledge.
All PCM samples are normalized to +-1.0, which means they contain the N MOST SIGNIFICANT bits of an 'infinite' resolution binary number, N being the number of bits in a sample minus 1 (the most significant bit is used as a sign). In other words, extending a 16 bit sample to 24 bits involves all of adding 8 zeros at the end, producing the exact same binary number. How did that hurt resolution? This is basic binary math.
However, to be a 16 bit converter, the bits have to be accurate to at least one more bit past the 16th bit, i.e. to at least half of the 16th bit or better. A 24 bit converter, theoretically, has to be accurate to half of the 24th bit, 256 times more accurate than a 16 bit converter when reproducing 16 bit samples. Again, how does this hurt things???
In the real world, actual 24 bit accuracy while maintaining the standard 2V RMS output is a near physical impossibility, so the BOTTOM and NOT the top bits (so you are dead wrong here and would know it if you had any notion of the most basic binary math, as in which bit carries which weight) in a 24 bit converter are not real because the actual resolution is more like 20-21 bits. That being said, that kind of converter is still 16-32 times more accurate in reproducing 16 bit samples than a 16 bit one, so again, how does this hurt 16 bit reproduction???
There is no such thing as a 16 to 24 bit 'modulator'. There is a 16 to 24 bit FILTER, for example an oversampling filter, which is not used if you only want to extend the bit depth at the same sample rate.
The reason for this is that filter coefficients are fractional numbers which, even for a filter operating on 16-bit input data, may not be accurately represented in 16, or for that matter 24, or for that matter infinite number of bits (like 1/3 cannot be represented in a finite number of decimal places). Digital filtering is a series of multiply-add operation on a first-in first-out buffer, and if one wants to keep thing accurate, it has to work with a lot more precision than the input data, in fact just reducing the coefficients to 16 bits may produce a worse filter and loss of precision on the output, so 40 or more bits was not uncommon even 25 years ago, while now 56 or 64 is the standard. Because 16 bit precise data multiplied by eg. 24 bit precise coefficients can generate results with more precision than 16 bits, the first filters had to reduce bit depth back to 16 bits at the output and of course apply proper dithering while doing it, in order to convert this data into analog using a 16 bit converter. As a result, a 16 bit DAC driven by a digital filter, driven by 16 bit samples, will lose about half a bit of precision. Soon after this first generation two methods were applied to counter this, which are using a more than 16 bit (18, 20 bit) ADC, and noise shaped dither, which pushed the loss of resolution into an ultrasonic region that the output filter after the DAC would almost completely remove, therefore preserving the maximum of the 16 bits of the data.
And while you are mentioning the venerable 1540, it was driven at a 4x rate with a noise shaped digital filter (one of the very first ones!) to actually attain virtually 16 bit resolution – because that's what proper noise shaped dithering can do, as long as there is extra bandwidth to push the noise into.
The current SD modulator based DACs do exactly the same thing, the difference is in the way the DAC attains high bit resolution, and in some cases this can open up more space for better dithering and noise shaping.
What about it? It is not a 8 bit PCM DAC nor is it accessible in any way except perhaps in DSD mode if the chip actually supports DSD data bypass, but then it only uses one bit input. It is usually a potentiometric DAC, which for N bits has N+1 states. Typically it's 6 to 8 bits and therefore has 7 to 9 states, around 3 bit resolution. It always has N=A bits 1 + B bits 0. The trick is that, for instance if 3 bits are on and 5 off, it randomly choses a different set of 3 bits out of the 8 available to be 1, for every sample where 3 bits are on and 5 off. What this does is statistically averages out the tolerances in the actual 8 bits – which should all be exactly equal, but since this is the real world, they are subject to tolerances.
More advanced chips actually use real 6 bit encoding and drive a 63-bit potentiometric DAC, to have even more bit elements to average out the imprecisions. This method of operation is commonly known as dynamic element matching. Why this high precision in a low bit DAC? This is because SD DACs trade amplitude precision for time precision by reducing the number of bits and driving them very fast with a bunch of noise shaping, BUT the actual bits still need to be very precise. This is because in theory to get each extra bit of resolution you need to increase the speed by a factor of two, without noise shaping. With noise shaping the factor drops down but faster than the requirement for precision for the actual real bits without noise shaping. Still, it is obviously much easier to get say 20 bit precision in 6 bits than in 20 bits! For instance using a 63 element potentiometric DAC to get 6 real bits of resolution will reduce the tolerance of a single element by a factor of around 5.6 (this is equal to about 2.5 bits more precision than a regular say R2R 6-bit DAC using the same elements).
If you had access to this DAC you would have to use it exactly as it is already been used to get the same result, everything else will be WORSE not better.
Completely wrong. Oversampling is done FIRST in order to get to a sample frequency which gives you enough space above the audio band to push enough of the quantization noise into the unused part by noise shaping as you next do bit depth reduction. Doig otherwise would result in loss of resolution right from the start and would be clearly audible and visible in measurements.
Some additional oversampling may occur without noise shaping and dithering at the highest sampling rate stages to implement more advanced dynamic element matching.
Weather the software is fixed point throughout has no relevance here. You can't get better than the actual resolution of a DAC chip at it's highest sampling rate by reducing the bit depth, period. Once you have reduced the bit depth, data is lost – the only question is how much and in what frequency range, and how it is decorrelated in order for it not to cause large losses in narrow bands but rather smaller losses smeared across wider bands (i.e. the loss has to convert to noise, not distortion and intermodulation). If your DAC is N bit accurate at your sampling rate and bit depth, regardless of how it got to that resolution, you can't get better than that by any noise shaping you can do externally overall. You may get a slightly better trade-off if you can apply more sophisticated noise shaping than the DAC itself between in band and out of band noise, assuming you can circumvent the built-in digital filters or trick them by concurrently upsampling the incoming material, or the incoming material is already 'content empty' in high frequency.
Which brings me to the astonishing amount of people who think they understand digital audio, and have no notion of noise shaping and dithering, would not recognize it looking directly at it. Many such a guru keeps showing us on youtube how it's hardly possible to hear any difference between 16 and 24 bit samples - while this might be true, the demos are downright wrong if not misleading.
One of them does so while wearing a wool hat over half an inch of hair covering his ears. He proceeds to demonstrate his thesis by reducing the bit depth in a well known audio processing program, keeping the sampling rate high. Then he says he can't hear a difference, but that there is one when looking at the file using a spectrogram view. And shows it to us as 'some sort of strange noise rising in frequency outside of the audio band'. Fortunately, his program is much more clever than he is and knowing it's stuff, applied proper noise shaped dither in an attempt to keep as much of the extra bits of resolution over the target 16 of the file in the audio band, so the typical noise shaping noise vs frequency distribution is nicely visible. He then proceeds to 'explain' this 'phenomenon' with 'I think' followed by sentences which have no base in reality, and must be so just because he 'thinks it'. I will remind readers that 'I think' means using the brain to think about the possible causes and evidence, and not using it to merely believe. Also, when doing such a demo use a file that actually has more than 6 bits of dynamic range, which you will actually notice if you make a path to your ears past the hair and woolen cap.
Again, completely wrong assumptions based on more assumptions as explained in the next to bottom paragraph.
How do you think 'other players' magically avoid quantization distortion? It's not like it's magic, it's just plain dithering. The difference is, with say 16 bits of resolution you can actually reduce volume to a point where you still cannot hear the distortion because you still have spare bits and with 8 bits you run out at -50dB or so, which is still clearly audible given a reasonably quiet ambient. With 16 bits, you still have 40dB or so to spare at -50dB volume, more than the instantaneous dynamics of a (really good!) human ear.
At full volume the sound is fine because the noise is some 50dB below, which is more than the instantaneous dymanic range of the human ear, and therefore imperceptible at that level unless in a completely different band.
Which brings me to the matter of dynamics and number of bits per sample. As SY eloquently said, sound reproduction is NOT sound recording. No-one needs real 24 bits of dynamic range while recording because no-one records in an underground anechoic chamber.
Let me use an example: 144 dB of dynamic range is letting you accommodate to the lack of sound in an anechoic isolation chamber to the point where you can hear your own bloodflow, and then firing a handgun 1 meter away from you. It can be done only once because it WILL result in hearing damage. Immagine getting that dynamic range with a very quiet (30dB background noise) recording venue – now the baseline is 30dB and the loudest noise would have to be 144dB over that – 174dB. At this loudness the recording session would last for about 1 second because everyone would be deaf after that, and this would surely make it difficult to continue, if the involontary spasming of your eye muscles due to your eyes and lungs vibrating to the noise would not. Yes, there are instruments that can generate astonishingly high sound pressures in peaks (120-130dB! and not good for the player of that instrument) but they last very short and this is measured to the absolute 0dB level, so relative to a quiet 30dB recording venue, this is 90-100dB – and 30dB is a VERY quiet recording venue.
Still, even if faithfully recorded, this sort of recording would be lost on the human ear in reproduction – even young and female ears are capable of at best 40-50dB instantaneous dynamics. In other words, if there is a loud peak, for a while later (in seconds) you will be completely deaf for anything 40-50dB quieter, while the ear adjusts again. It reacts much faster to attacks than to decays, and in reality you are lucky if you can manage 30dB of instantaneous dynamics.
In other words, 24 bits are there to accommodate various relative levels needed in mixing the various recorded channels, plus processing. Nowadays the most convenient format is 32-bit fixed point, which is used for processing usually by extending the range by some bits on the most significant end, depending on the number of channels on the mixer (16 channels, 4 bits – because a full scale input on all channels will generate a 16x larger output worst case, for which 4 bits are needed to prevent clipping). The rest of the bits are used as a 'gutter' for accruing errors due to processing with a finite resolution. Once the mix is done, everything is normalized back to +-1 (MSB aligned) and the final reduction in bit depth is done if needed (which of course includes proper noise shaped dithering).
Arguably, real reproduction circumstances make anything over 16 bits superfluous, though it could also be argued that extra bandwidth (higher sampling rate) is beneficial to a degree – however with proper noise shaped dither applied, the requirements are not as great as one would imagine, 24/96 is already overkill. The reason is found in the normalized curves for the sensitivity of the human ear (1 of them) vs frequency. Even so, some extra bandwidth is good because the human hearing is based on earS (2 of them) being able to discern differences in phase and delay smaller than the raw bandwidth of a single ear would suggest. This would lead us to discussions about DSD but that is outside the scope here.
The point is, while more than 16 bits of bit depth may be overkill, in today's world of abundant storage and 64-bit wide CPUs the most convenient data width that is over 16 bits is 32, and the amount of data on a 1 hour CD is considered 'not so bad' so 32-bit and higher sampling rates are here to stay even as a transport format, though it's largely empty or noise-filled.
And an even more dubious assumption. Yes, some software will apply all sorts of mediocre signal processing without telling you, but which software does not or the processing is avoidable, is fairly common knowledge.
Software is often 32-bit floating point which is technically a complete bodge of a 'solution', given that it requires repacking of data (and associated time lost) and provides 24 bit resolution WITHOUT any real data protection from overflows or rounding error creepage. In fact, both of these phenomena will result in loss of precision. While the floating point number range is huge, the precision of each number is only 23 binary digits plus sign – just like the native 24-bit PCM. 32-bit integer would have been a better choice. However, when DSP-like instructions were added to the Intel CPU instruction set, in form of MMX/3Dnow instructions (and later derivatives), they could only be added to the floating point unit while retaining compatibility. So, today, 18 years later we are still victims of that decision, fortunately most serious programs will now use double precision float and get about 48 bits of resolution.
If your program uses 32-bit float, you better disable all processing if you want to retain 24 bit resolution (as to how much it matters, see above paragraph).
The initial assumption is dubious because 32-bit or for that matter any bit floating point is NOT native to any audio DAC. Neither does the 'audio card' apply any filters or interprets anything to apply any filters, this is entirely driven by how the DAC on the audio card is implemented and what options were selected for it's integration onto the card.
This brings us to the 'problem' of higher sampling rates. This primarily has to do with the requirement for brick wall filtering if you want your ADC to produce standard PCM encoding, and your DAC to convert it to analog. The initial 44.1 CD format left a very narrow 2.05kHz range (and assumed a 20kHz bandwidth) into which one had to squeeze a filter that drops the signal 96dB – the equivalent of a 159th order filter expressed in classical analog terms. This is not a trivial matter to implement even with digital filtering and get anything approaching good time domain response. In the analog domain it is close to impossible and doubly more so because you need two exactly equal ones, one for each channel. Doubling the sampling rate to 88.1k increases this transition range to a comparatively massive 46.15kHz – a 22.5 fold increase, severely relaxing the requirements for the filter – even while increasing the usable bandwidth. Even more so with further increases to 96k, 176.4 or 192k – all well known from the olden days of 4x oversampling. Because you actually WANT to increase the bandwidth and not oversample an existing low sampling rate signal, you do not need a brick wall filter at the ADC nor the DAC – a much less severe one is needed and this can be designed for excellent time domain response far above what anyone is able to hear.
It should be noted that the time response you can get is defined ultimately by the sampling rate, not the bit depth. Because of this, DSD is many times more accurate in the time domain than even the highest used PCM – but this comes at a trade-off in resolution in order to keep the amount of data in reasonable limits, and it assumes it was not derived from a PCM master.
In most cases the filtering chosen inside the DAC – and these days all DACs have it built in (and be thankful for that because the people that had to build those first brick wall filters in the analog domain would probably strangle you given the same task again instead of implementing it digitally) – is done based on the sample rate, since it is assumed that the first 20k of the available bandwidth are of most interest. Digital filters scale with sampling rate but the absence of need for a brick wall filter for higher sample rates has made most manufacturers provide more relaxed and time domain accurate filters for sampling rates above 64k.
Now, if a sound card chooses to apply extra processing, this is it's own fault – however, in most cases a serious PC audio system does not use a sound card but rather some sort of data bridge to convert a stream as read from a file to either SPDIF or I2S in the end, possibly using other transport methods on the way (such as USB). All of these have their own problems, none of which have to do with the actual DA conversion – though the quality of the DAC output can be impaired along the 'garbage-in = garbage-out' principle.
Again, completely wrong – the process of extending bit depth is 'plain' and trivial with no loss (you would have to be truly amazingly incompetent to get it wrong) while reducing bit depth is DEFINITELY NOT just 'plain truncation'. Plain truncation is exactly what makes it sound bad, which is why dithering is needed in the first place.
So what kind of an opinion should one have of ideas which are based on assumptions where every single assumption is wrong? See above under 'garbage in = garbage out' principle.
A lot of what you wrote I am already in agreement, I understand most of it.
The order of how DSM worked wasn't important just the end result. I like to think whole-fully electrically. It's clear that DSM are really good performers, but compromises are made to get there. I'd much prefer a digital filter (if any) operating systematically (equal to or less but never more than the) input bit depth, with minimal processing than trust some dubious up sampling routines (linear phase? apodising?), which are usually 24bit. At the very end, the interface that joins digital and electrical is almost always fixed point, so I personally dislike anything floating point, it's 'iffy' having it anywhere in the path of PCM, something about that dyn. range of 1000db and the conversion to/from PCM. One example I will highlight was an observation I made with floating point plug-in enabled on another popular 'audio player' with a facility to preview the audio spectrum via means of FFT.
By adding 'dither' to the signal path becomes apparent on the FFT analyser, what I witnessed was that the noise would compand with the signal! i.e. Optimal noise (the d-word) should be steady-state, uncorrelated from the signal (not signal-dependent).
Of course there will always be good and rushed implementations but It seems, older 100% fixed point digital synths from the early 90s have a lot more core sound. This is one small observation for a amateur like myself to notice to make, but it makes me question what software is really doing to the signal these days. And this is why overall I trust more to have hardware centric DSP like pro-tools or sonic core over software DSP based system overall.
The order of how DSM worked wasn't important just the end result. I like to think whole-fully electrically. It's clear that DSM are really good performers, but compromises are made to get there. I'd much prefer a digital filter (if any) operating systematically (equal to or less but never more than the) input bit depth, with minimal processing than trust some dubious up sampling routines (linear phase? apodising?), which are usually 24bit. At the very end, the interface that joins digital and electrical is almost always fixed point, so I personally dislike anything floating point, it's 'iffy' having it anywhere in the path of PCM, something about that dyn. range of 1000db and the conversion to/from PCM. One example I will highlight was an observation I made with floating point plug-in enabled on another popular 'audio player' with a facility to preview the audio spectrum via means of FFT.
By adding 'dither' to the signal path becomes apparent on the FFT analyser, what I witnessed was that the noise would compand with the signal! i.e. Optimal noise (the d-word) should be steady-state, uncorrelated from the signal (not signal-dependent).
Of course there will always be good and rushed implementations but It seems, older 100% fixed point digital synths from the early 90s have a lot more core sound. This is one small observation for a amateur like myself to notice to make, but it makes me question what software is really doing to the signal these days. And this is why overall I trust more to have hardware centric DSP like pro-tools or sonic core over software DSP based system overall.
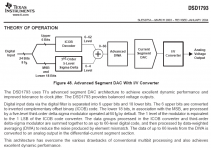
In addition to my original post, the PCM1793 does what's described, passing the top 6bit's 'unscathed' by the modulator onto the current section.
God knows what ICOB and DWA does to the signal.
See this info-graphic in the marketing material for the iFi nano.
It's also re-assuring to see a real product which allows control of the phase behavior of the interpolation filter, as a toggle on the device itself.
I'm think most ICs work this way, pass those significant bits, as I stated in OP. Finding them and then the product they're enclosed is harder to do however.
Any comments?
(Although quite old, see also relevant page of 1793 ds).
God knows what ICOB and DWA does to the signal.
See this info-graphic in the marketing material for the iFi nano.
It's also re-assuring to see a real product which allows control of the phase behavior of the interpolation filter, as a toggle on the device itself.
I'm think most ICs work this way, pass those significant bits, as I stated in OP. Finding them and then the product they're enclosed is harder to do however.
Any comments?
(Although quite old, see also relevant page of 1793 ds).
Attachments
Last edited:
As Ilimzn explained in great detail, you are only making things worse by doing this. You have a lot of misconceptions and it is only going to lead to worse sound. There is nothing lost or altered at all in feeding a 16-bit word to a 24-bit DAC or 32-bit filter. It will be properly aligned unless something is configured incorrectly. It seems like you don't understand the difference between an MSB and an LSB. BTW, there is no reason to fear floating point numbers, but you'll still find most interpolating filters are implemented with fixed point math I think.
Last edited:
- Status
- Not open for further replies.