Haii
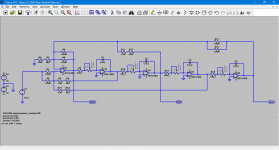
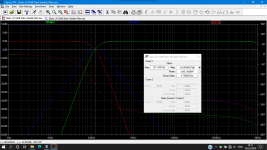
would you help us to create a response formula or curve from this simple state variable filter scheme.
like Linkwitz riley, Butterworth, Bessel and Chebyshev.
below I attached an example but I forgot where the source came from.
would you help us to create a response formula or curve from this simple state variable filter scheme.
like Linkwitz riley, Butterworth, Bessel and Chebyshev.
below I attached an example but I forgot where the source came from.
Attachments
Hi,
TexasInstruments offered a Universal Active Filter, the UAF42.
The datasheet and description presented formulas and design examples which may help.
jauu
Calvin
TexasInstruments offered a Universal Active Filter, the UAF42.
The datasheet and description presented formulas and design examples which may help.
jauu
Calvin
Hii
Calvin
looks interesting. after I read this chip datasheet a filter with slope about 12dB. but the design equations is quite interesting. maybe I need time to learn it
Regards
Dimas
Calvin
looks interesting. after I read this chip datasheet a filter with slope about 12dB. but the design equations is quite interesting. maybe I need time to learn it
Regards
Dimas
It is a very smart design, I like it a lot.
It doesn't make sense to modify The Q-factor, because only LR has a flat sum with identical frequencies, which it is.
One problem is the noise, about 15 times of a single opamp, because of the feedback attenuators and high resistor values.
I scaled down the Rs to 1/5 and the noise went down to half with 5532.
Another problem is by principle when you connect the midbass its -3dB low end will be on or very close to the crossover frequency giving ugly peaks and dips in the sum. A 12dB HP Q=0.71 together with the speaker fall-off would result in a perfectly flat response.
I fiddled around to get a 12dB curve out and found out that the outputs of the 1st -2nd +3rd opamp give a 12dB HP curve, but only Q=0,5 is possible. This works with a closed speaker with Q=1 to form again a flat sum.
Has the advantage of small enclosure.
It doesn't make sense to modify The Q-factor, because only LR has a flat sum with identical frequencies, which it is.
One problem is the noise, about 15 times of a single opamp, because of the feedback attenuators and high resistor values.
I scaled down the Rs to 1/5 and the noise went down to half with 5532.
Another problem is by principle when you connect the midbass its -3dB low end will be on or very close to the crossover frequency giving ugly peaks and dips in the sum. A 12dB HP Q=0.71 together with the speaker fall-off would result in a perfectly flat response.
I fiddled around to get a 12dB curve out and found out that the outputs of the 1st -2nd +3rd opamp give a 12dB HP curve, but only Q=0,5 is possible. This works with a closed speaker with Q=1 to form again a flat sum.
Has the advantage of small enclosure.
Hii.. Bansuri
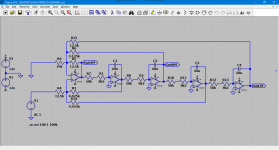
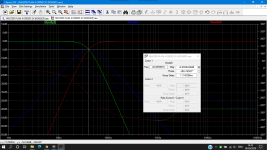
Yes. this use is indeed due to the "thermal noise resistor" which is quite high because I adjusted the JFET Op Amp like TL082 which in my place this Op Amp has a preferred low frequency character so that noise is somewhat ignored due to crossover damping. when using op amp low distortion 5532N/MC33070 there is a change in the resistor value. as follows
Yes. this use is indeed due to the "thermal noise resistor" which is quite high because I adjusted the JFET Op Amp like TL082 which in my place this Op Amp has a preferred low frequency character so that noise is somewhat ignored due to crossover damping. when using op amp low distortion 5532N/MC33070 there is a change in the resistor value. as follows
Attachments
- Home
- Source & Line
- Analog Line Level
- 24dB State Variable Filter