The reason I'm using 4 lm317s is basically to spread the heat between them (and also the 220r voltage dropping resistor) because it's tricky to fit a heatsink on the PCB inside the radford chassis, as they're not very tall. I would have preferred the one but this seems to work just fine. Testing the CCS parts separately reveals they match within 0.2mA
It would not matter if they did not match at all. A 5mA CCS in parallel with a 12mA CCS is a 17mA CCS!
Sorry, I meant between each valve's compound CCS of four LM317s (8 in total for one channel), so the transformer ends up with a very small DC imbalance indeed!
Last edited:
Just so that the valves are always biased exactly right 🙂 It's probably not even necessary, I just like the idea!
The OPT is just a standard EI core (it's a Radford STA15)
The OPT is just a standard EI core (it's a Radford STA15)
CCS bias seems popular these days, but in my opinion is unnecessary and, as you have found, leads to LF problems. Even without feedback it could cause excessive LF phase shift.
Why is 'exactly right' bias not worth pursuing? Two reasons:
1. In looking for the right bias point (whether from datasheets, measurements or listening) you will find a broad compromise between conflicting pressures. 5% or 10% change in current will not usually have much effect.
2. Valves vary, both between different samples and as they age. Maybe 10% to 20% difference? There is no reason to suppose that keeping rigidly to a particular quiescent current will get the best out of any valve at any stage in its life. It might even create problems as the bias voltage adjusts itself to get the 'right' current - clipping on peaks in some designs?
I have to smile when I see designs, both DIY and commercial, where peculiar resistor values are given to 3 significant figures. This gives a spurious air of precision design, when in fact it is merely pretentious. Except in RIAA networks, E12 series at 5% tolerance is fine - for many purposes 10% tolerance is good enough.
For an output stage I would use a combination of fixed and cathode resistor bias. The fixed part increases headroom a little and, if adjustable, copes with valve variation. It also reduces the extent to which the bias shifts with signals due to second-order distortion, so you can run valves cooler. The resistor part protects against bias supply failure.
So I would get rid of the CCS. Rectify your heater supply to get some negative voltage and use that to reduce the value of the cathode resistors. Run the valves a little cooler than the original design - you should get a bit less third-order distortion and they will last longer.
Why is 'exactly right' bias not worth pursuing? Two reasons:
1. In looking for the right bias point (whether from datasheets, measurements or listening) you will find a broad compromise between conflicting pressures. 5% or 10% change in current will not usually have much effect.
2. Valves vary, both between different samples and as they age. Maybe 10% to 20% difference? There is no reason to suppose that keeping rigidly to a particular quiescent current will get the best out of any valve at any stage in its life. It might even create problems as the bias voltage adjusts itself to get the 'right' current - clipping on peaks in some designs?
I have to smile when I see designs, both DIY and commercial, where peculiar resistor values are given to 3 significant figures. This gives a spurious air of precision design, when in fact it is merely pretentious. Except in RIAA networks, E12 series at 5% tolerance is fine - for many purposes 10% tolerance is good enough.
For an output stage I would use a combination of fixed and cathode resistor bias. The fixed part increases headroom a little and, if adjustable, copes with valve variation. It also reduces the extent to which the bias shifts with signals due to second-order distortion, so you can run valves cooler. The resistor part protects against bias supply failure.
So I would get rid of the CCS. Rectify your heater supply to get some negative voltage and use that to reduce the value of the cathode resistors. Run the valves a little cooler than the original design - you should get a bit less third-order distortion and they will last longer.
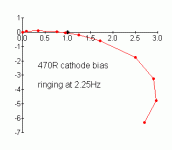
You could try just dropping in 470R cathode resistors instead of the CCS's, just to see if they are the cause of the LF instability or not. Pretty complex design that schem, hope it sounds good? Let us know...
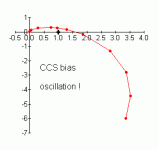
I have put together a quick spreadsheet models, using typical values for LF poles in an amplifier of the Mullard/Radford/Leak topology. I did two versions, one for CCS bias, the other for resistor bias. Without any cheating, the CCS one shows LF oscillation and the resistor one shows extremely marginal stability with serious peaking at 2.25Hz.
The results are in the attachments. Stability requires that the line does not wrap around the 1.0 point on the X-axis.
The step network feeding the PS in the Radford would improve things, which may be why it is there, but in any case the situation is marginal.
The results are in the attachments. Stability requires that the line does not wrap around the 1.0 point on the X-axis.
The step network feeding the PS in the Radford would improve things, which may be why it is there, but in any case the situation is marginal.
Attachments
Last edited:
DF96, very clever, and surprisingly close to reality! The 470R does indeed ring slightly. Out of interest, how did you produce these graphs and what do they represent?
The graph is a plot of real (x) and imaginary 👍 component of the loop gain at low frequencies. I think this is called a Bode plot. The loop gain is A x b, where A is the amplifier gain and b is the feedback. For simplicity I assumed b=1. A at mid-band was 25 - this represents an amplifier with, say, open loop gain 500 and closed loop gain 20.
I then calculated the amplitude and phase of a set of high pass filters: phase splitter, o/p stage coupling, o/p stage cathode, and OPT. I just picked typical values for each:
PS 560K, 0.47uF (0.6Hz)
o/p grid 470K, 0.22uF (1.5Hz)
o/p cathode gm 12.5mA/V i.e. 80 ohms, plus 470uF and CCS (4.2Hz), or 470uF and 470R (4.2Hz/0.7Hz)
OPT -3dB at 20Hz (20Hz)
The 470R cathode resistor turns that HPF into a lead-lag network with less phase shift but higher LF gain. Add up the phase shifts, multiply up the amplitudes, and then plot the results. The closer the curve goes to the 1.0 point the higher the peak in response, at roughly the frequency of closest approach. If the curve circles the point then you get oscillation. If you want to know more your best option is to Google for feedback stability, servo systems, Bode plots. I think Mr. Nyquist had something to say too.
In olden days before spreadsheets they used to do this sort of thing using graph paper. There are short cuts and approximations which can give a good idea.
The quick and easy way to stability is to have a dominant pole - in our case the OPT. Then ensure that all other poles are well away in frequency. You really want the next pole to be down by a ratio of about the mid-band loop gain (i.e. 0.8Hz). The nearest one is the o/p cathode at 4.2Hz. This is much too close so either needs reducing with an even bigger capacitor (2200uF?), or partially cancelling by turning it into a lead-lag with a resistor instead of CCS. That is how they used to get away with such small decouplers. Alternatively, reduce the feedback which will increase the sensitivity and distortion.
Interesting thought: an amplifier with LF problems caused by feedback (i.e. most of them, as this problem is often overlooked) is likely to sound lumpy even when it doesn't actually oscillate, so is this why people don't like feedback?
I then calculated the amplitude and phase of a set of high pass filters: phase splitter, o/p stage coupling, o/p stage cathode, and OPT. I just picked typical values for each:
PS 560K, 0.47uF (0.6Hz)
o/p grid 470K, 0.22uF (1.5Hz)
o/p cathode gm 12.5mA/V i.e. 80 ohms, plus 470uF and CCS (4.2Hz), or 470uF and 470R (4.2Hz/0.7Hz)
OPT -3dB at 20Hz (20Hz)
The 470R cathode resistor turns that HPF into a lead-lag network with less phase shift but higher LF gain. Add up the phase shifts, multiply up the amplitudes, and then plot the results. The closer the curve goes to the 1.0 point the higher the peak in response, at roughly the frequency of closest approach. If the curve circles the point then you get oscillation. If you want to know more your best option is to Google for feedback stability, servo systems, Bode plots. I think Mr. Nyquist had something to say too.
In olden days before spreadsheets they used to do this sort of thing using graph paper. There are short cuts and approximations which can give a good idea.
The quick and easy way to stability is to have a dominant pole - in our case the OPT. Then ensure that all other poles are well away in frequency. You really want the next pole to be down by a ratio of about the mid-band loop gain (i.e. 0.8Hz). The nearest one is the o/p cathode at 4.2Hz. This is much too close so either needs reducing with an even bigger capacitor (2200uF?), or partially cancelling by turning it into a lead-lag with a resistor instead of CCS. That is how they used to get away with such small decouplers. Alternatively, reduce the feedback which will increase the sensitivity and distortion.
Interesting thought: an amplifier with LF problems caused by feedback (i.e. most of them, as this problem is often overlooked) is likely to sound lumpy even when it doesn't actually oscillate, so is this why people don't like feedback?
Thanks very much for you input so far!
Do you think I could cheat by changing C6 to 100nF instead of 1uF, creating the dominant pole there instead? (Feeding some of the LF to the other side of the phase splitter "early" to cancel it out)
I'd rather do as little hacking to these PCBs as possible!
Do you think I could cheat by changing C6 to 100nF instead of 1uF, creating the dominant pole there instead? (Feeding some of the LF to the other side of the phase splitter "early" to cancel it out)
I'd rather do as little hacking to these PCBs as possible!
No, C6 is fine. That pole is well clear, although there might be a small advantage in increasing C6. The dominant pole is the OPT, and there is not much you can do about that in a hi-fi amp. It is the next one down that is the trouble - output cathode. Two options: increase the cathode decoupler to get this pole down, go back to a resistor.
Note that the original design was stable with only 50uF here, because they used a resistor. The pole was around the same frequency as the OPT but had the sting taken out of it by a nearby zero.
Something else to try is either increasing or reducing C4. At present it seems to put a lead-lag right in the critical region, so it might help to move it away up or down. Try changing the 50uF for either 10uF or 220uF.
However, my basic advice hasn't changed: ditch the CCS! As well as creating LF problems it more or less guarantees that the o/p stage bias will be wrong whenever there is a signal present. This is because it fixes average current when what you actually need is fixed quiescent current. Or if you must have a CCS, have a combined CCS with no bypass capacitor in order to force perfect push-pull working. You lose DC balance but gain AC balance. You would then need well-matched output valves.
Note that the original design was stable with only 50uF here, because they used a resistor. The pole was around the same frequency as the OPT but had the sting taken out of it by a nearby zero.
Something else to try is either increasing or reducing C4. At present it seems to put a lead-lag right in the critical region, so it might help to move it away up or down. Try changing the 50uF for either 10uF or 220uF.
However, my basic advice hasn't changed: ditch the CCS! As well as creating LF problems it more or less guarantees that the o/p stage bias will be wrong whenever there is a signal present. This is because it fixes average current when what you actually need is fixed quiescent current. Or if you must have a CCS, have a combined CCS with no bypass capacitor in order to force perfect push-pull working. You lose DC balance but gain AC balance. You would then need well-matched output valves.
I wish I could understand the maths behind poles and zeros - I barely really know what they are, I know that they're related to the position of a rolloff and its corresponding phase shift but I'd like to have a deeper understanding of the mathematics so I could calculate this myself! I know it involves complex numbers and matrices, something I need to learn still...
Each roll-off, HF or LF, has a pole at the corner frequency. In addition, each high-pass roll-off has a zero at the origin, but this can usually be ignored. A lead-lag has a pole and a zero, at the two corner frequencies. I think the pole is at the higher amplitude corner, but I may have got that the wrong way round.
To do all this properly you need complex numbers, but you can get quite a long way without. Just remember that the shape of any first-order roll-off (i.e. 6dB/octave) in terms of amplitude and phase is exactly the same, so universal curves apply. You just have to scale by frequency.
To do all this properly you need complex numbers, but you can get quite a long way without. Just remember that the shape of any first-order roll-off (i.e. 6dB/octave) in terms of amplitude and phase is exactly the same, so universal curves apply. You just have to scale by frequency.
- Status
- Not open for further replies.
- Home
- Amplifiers
- Tubes / Valves
- 1Hz oscillation with CCS biased output valves