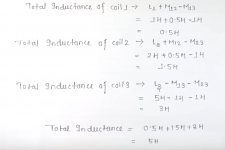Assuming a transformer with a split primary and a known end to end inductance, I feel pretty good about the following.
Total primary inductance is made up of L1+L2+2M
M = K √(L1 L2)
Where I get lost is more than two series primary windings on the same core
Assuming I have 4 windings in the primary and want to work out M, would it be
M = K √(L1 L2 L3 L4)?
Is total end to end inductance then L1+L2+L3+L4+2M?
Assuming I am wrong with the second half (Likely) can you help me with corrections to the formulas?
Thanks,
Marty
Total primary inductance is made up of L1+L2+2M
M = K √(L1 L2)
Where I get lost is more than two series primary windings on the same core
Assuming I have 4 windings in the primary and want to work out M, would it be
M = K √(L1 L2 L3 L4)?
Is total end to end inductance then L1+L2+L3+L4+2M?
Assuming I am wrong with the second half (Likely) can you help me with corrections to the formulas?
Thanks,
Marty
Inductance is Directly Proportional to (Turns) Squared.
2 times the turns = 4 times the inductance
For windings, connected in series, and connected in phase:
1 primary, 1 turn: Inductance is Unity (Call it Unity)
2 primaries, 1 turn each, 2 turns: Inductance is 4X Unity
3 primaries, 1 turn each, 3 turns: Inductance is 9X Unity
4 primaries, 1 turn each, 4 turns: Inductance is 16X Unity
1 primary, 1 turn, another primary 3 turns: Inductance is 16X Unity
Does that explain it?
Careful, the saturation of the core is according to Amp x Turns.
For the same current, 2 times the turns, will saturate at 1/2 the current of 1 times the turns.
2 times the turns = 4 times the inductance
For windings, connected in series, and connected in phase:
1 primary, 1 turn: Inductance is Unity (Call it Unity)
2 primaries, 1 turn each, 2 turns: Inductance is 4X Unity
3 primaries, 1 turn each, 3 turns: Inductance is 9X Unity
4 primaries, 1 turn each, 4 turns: Inductance is 16X Unity
1 primary, 1 turn, another primary 3 turns: Inductance is 16X Unity
Does that explain it?
Careful, the saturation of the core is according to Amp x Turns.
For the same current, 2 times the turns, will saturate at 1/2 the current of 1 times the turns.
Last edited:
Not necessarily. If, in example, one set of turn is reverse wound, inductance is null.
What you need is to write down an entire set of equations and solve then. If you have L1, L2, L3 and L4, each one of them will have a particular k to the others. Assuming that all them are wound in the same sense and in a common core, k will be close to 1.
The formula squaring root of the product of the 4 inductances is wrong as it gives values of Hy^2 which ovbiously isn't inductance. At first time I would be near the sum of the dual products and sqrt of the 4 members added.
What you need is to write down an entire set of equations and solve then. If you have L1, L2, L3 and L4, each one of them will have a particular k to the others. Assuming that all them are wound in the same sense and in a common core, k will be close to 1.
The formula squaring root of the product of the 4 inductances is wrong as it gives values of Hy^2 which ovbiously isn't inductance. At first time I would be near the sum of the dual products and sqrt of the 4 members added.
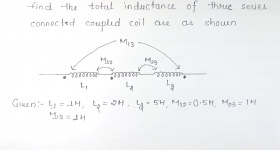
You only need same formula of one pairs of mutually coupled coils for 4 coils, M12, M23, M34, M14 are calculated and added together taken polarity into account.
6. CALCULATION OF TOTAL INDUCTANCE THREE SERIES COUPLED COILS || NUMERICAL PROBLEM ON DOT ON COILS|| - YouTube
6. CALCULATION OF TOTAL INDUCTANCE THREE SERIES COUPLED COILS || NUMERICAL PROBLEM ON DOT ON COILS|| - YouTube
Attachments
Thank you all for the replies and a special thanks to koonw for providing a perfect link and screen shots.
Well, yes, but then that transformer is wired WRONG (out of phase windings) and UNUSABLE.
Nobody will use it that way.
Osvaldo de Banfield,
I said windings connected in series, and in-phase.
It does not matter . . . straight wound, or reverse wound, it just has to be connected serially in-phase.
Right?
I said windings connected in series, and in-phase.
It does not matter . . . straight wound, or reverse wound, it just has to be connected serially in-phase.
Right?
I used this phrase to meaning that not allways increasing turn increase inductance. It also depends on coupling factor and winding sense. Obviously reverse winding has no practical sense in transformers or chokes but in non inductive resistors.
Hopefully all output transformers are well enough designed so that the coupling factor of all the primary windings at low frequencies is excellent.
(high frequency coupling is another matter).
That means that the low frequency limit caused by limited inductance would follow the simple rule . . . Total Turns Squared.
For example, Twice the turns = 4 times the inductance.
But then there also is the limit of inductance which is related to all the details of the laminations.
(high frequency coupling is another matter).
That means that the low frequency limit caused by limited inductance would follow the simple rule . . . Total Turns Squared.
For example, Twice the turns = 4 times the inductance.
But then there also is the limit of inductance which is related to all the details of the laminations.