Hello everyone,
I am currently researching the active three-way crossover scheme proposed by Duelund (referenced on the Linkwitz website) https://www.linkwitzlab.com/crossovers.htm and would appreciate your insights on two design approaches. Below, I outline the configurations and my findings for discussion:
Configuration 1: Current Implementation
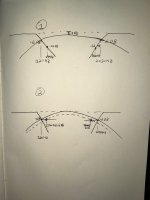
Bass/Treble Filters: Two cascaded 2nd-order filters per driver,Individual 2nd-order filters: -6dB points at 190 Hz (bass)and 1310 Hz (treble).
Cascaded result: -6dB crossover points at 120 Hz and 2050 Hz .
Midrange Filter: A 2nd-order Linkwitz-Riley high-pass (120 Hz) and low-pass (2050 Hz).
Simulation Observation:A slight 1dB dip at 500 Hz due to filter interaction.When the acoustic centers are aligned and midrange polarity is inverted, it might seems no discernible impact on sound quality. ?
Configuration 2:
Midrange Adjustment: Shift the -6dB points to 140 Hz and 1800 Hz.
Theoretical Response: Midrange attenuation reaches -7dB at the original crossover points (120 Hz/2050 Hz). When rising the midrange gain by 1dB flattens the response to 0dB at 500 Hz while maintaining -6dB at the crossover points (solid curve in Figure 2). This matches the curve in linkwitz website , seems it aligns with the original design philosophy.
Is my interpretation of Configuration 2 accurate in replicating Linkwitz’s intended response?
Which configuration (1 or 2) is preferable in terms of Phase coherence and group delay and Acoustic center alignment requirements?
Does Configuration 2 impose stricter requirements for acoustic center alignment compared to Configuration 1?
Attached are the simulated response curves for reference. Your expertise on these matters would be invaluable to my project. Thank you in advance for your time and insights.
Best regards,
Zack
I am currently researching the active three-way crossover scheme proposed by Duelund (referenced on the Linkwitz website) https://www.linkwitzlab.com/crossovers.htm and would appreciate your insights on two design approaches. Below, I outline the configurations and my findings for discussion:
Configuration 1: Current Implementation
Bass/Treble Filters: Two cascaded 2nd-order filters per driver,Individual 2nd-order filters: -6dB points at 190 Hz (bass)and 1310 Hz (treble).
Cascaded result: -6dB crossover points at 120 Hz and 2050 Hz .
Midrange Filter: A 2nd-order Linkwitz-Riley high-pass (120 Hz) and low-pass (2050 Hz).
Simulation Observation:A slight 1dB dip at 500 Hz due to filter interaction.When the acoustic centers are aligned and midrange polarity is inverted, it might seems no discernible impact on sound quality. ?
Configuration 2:
Midrange Adjustment: Shift the -6dB points to 140 Hz and 1800 Hz.
Theoretical Response: Midrange attenuation reaches -7dB at the original crossover points (120 Hz/2050 Hz). When rising the midrange gain by 1dB flattens the response to 0dB at 500 Hz while maintaining -6dB at the crossover points (solid curve in Figure 2). This matches the curve in linkwitz website , seems it aligns with the original design philosophy.
Is my interpretation of Configuration 2 accurate in replicating Linkwitz’s intended response?
Which configuration (1 or 2) is preferable in terms of Phase coherence and group delay and Acoustic center alignment requirements?
Does Configuration 2 impose stricter requirements for acoustic center alignment compared to Configuration 1?
Attached are the simulated response curves for reference. Your expertise on these matters would be invaluable to my project. Thank you in advance for your time and insights.
Best regards,
Zack
Attachments
Hello,
I read by this article a long time ago, interesting but it is theory. You should test with a dsp to choose the best sonic solution. The best result depends on your tools and materials.
To apply active crossover I understood you should always align acoustics center and you should linearize acoustic response of driver if necessary. Here the mid has a 6dB acoustic slope not easy to achieve without linearization.
We are interested by your results 🙂
Best regards.
I read by this article a long time ago, interesting but it is theory. You should test with a dsp to choose the best sonic solution. The best result depends on your tools and materials.
To apply active crossover I understood you should always align acoustics center and you should linearize acoustic response of driver if necessary. Here the mid has a 6dB acoustic slope not easy to achieve without linearization.
We are interested by your results 🙂
Best regards.
I am a great fan of Duelundish acoustic xo for multiway dsp-speakers. Mid-tweeter can be too difficult because of mid's resonances and dispersion.
The challenge is to control each driver's response/phase at least 1,5 octave beyond the xo, so that eg. in a 3-way woofer and tweeter sum well below the mid! Basically LR2 so the mid has reverse polarity.
More theoretical background by John Kreskovsky
https://musicanddesign.speakerdesign.net/tech.html
https://musicanddesign.speakerdesign.net/Duelund_and_Beyond.html
The challenge is to control each driver's response/phase at least 1,5 octave beyond the xo, so that eg. in a 3-way woofer and tweeter sum well below the mid! Basically LR2 so the mid has reverse polarity.
More theoretical background by John Kreskovsky
https://musicanddesign.speakerdesign.net/tech.html
https://musicanddesign.speakerdesign.net/Duelund_and_Beyond.html
If I understand it correctly, you want to implement Linkwitz's approximation to Duelund. Quoting the site you linked to:
"a) Crossover frequencies at 0.24 and 4.1 (e.g. at 120 Hz and 2050 Hz)
Crossover points are at -6 dB.
Filter outputs are in phase when the midrange bandpass has reversed polarity.
Bandpass is centered at normalized frequency 1.0 (e.g. at 500 Hz).
b) Woofer lowpass LPD3 = 0.384 / ( s + 0.38)4
Four real axis poles at -0.38 which can be realized with two LR2 lowpass filters in cascade (e.g. at 190 Hz).
c) Midrange bandpass BPD3 = -15s2 / [(s + 0.28)2 (s + 3.6)2]
Two zeros at the origin and two poles at -0.28 can be realized with a single LR2 highpass filter (e.g. at 140 Hz).
The two poles at -3.6 can be realized with one LR2 lowpass (e.g. at 1800 Hz). It is in cascade with the LR2 highpass.
d) Tweeter highpass HPD3 = s4 / (s + 2.62)4
Four zeros at the origin and four poles at -2.62 can be realized with two LR2 highpass filters in cascade (e.g. at 1310 Hz)."
I think that matches your configuration 2. Linkwitz also tweaked the bandpass gain to get a flattish summed response.
I don't understand what the advantage is supposed to be compared to three-way Linkwitz-Riley. You can get rid of the all-pass section you need for three-way Linkwitz-Riley, but you pay for that with having to use some very specific ratio of the crossover frequencies.
Linkwitz had some interesting ideas on how to correct for the roll-off of the drivers, near the bottom of the page you linked to.
"a) Crossover frequencies at 0.24 and 4.1 (e.g. at 120 Hz and 2050 Hz)
Crossover points are at -6 dB.
Filter outputs are in phase when the midrange bandpass has reversed polarity.
Bandpass is centered at normalized frequency 1.0 (e.g. at 500 Hz).
b) Woofer lowpass LPD3 = 0.384 / ( s + 0.38)4
Four real axis poles at -0.38 which can be realized with two LR2 lowpass filters in cascade (e.g. at 190 Hz).
c) Midrange bandpass BPD3 = -15s2 / [(s + 0.28)2 (s + 3.6)2]
Two zeros at the origin and two poles at -0.28 can be realized with a single LR2 highpass filter (e.g. at 140 Hz).
The two poles at -3.6 can be realized with one LR2 lowpass (e.g. at 1800 Hz). It is in cascade with the LR2 highpass.
d) Tweeter highpass HPD3 = s4 / (s + 2.62)4
Four zeros at the origin and four poles at -2.62 can be realized with two LR2 highpass filters in cascade (e.g. at 1310 Hz)."
I think that matches your configuration 2. Linkwitz also tweaked the bandpass gain to get a flattish summed response.
I don't understand what the advantage is supposed to be compared to three-way Linkwitz-Riley. You can get rid of the all-pass section you need for three-way Linkwitz-Riley, but you pay for that with having to use some very specific ratio of the crossover frequencies.
Linkwitz had some interesting ideas on how to correct for the roll-off of the drivers, near the bottom of the page you linked to.
For accuton c168-6-890 or scan 8531 speakers, working at this frequency should be pleasant and appropriate, the only downside should be their price😀
For the 4order Linkwitz Raily application, the Duelund variant of the midrange bandpass filter has fewer operational amplifiers and smoother group delay, although I doubt if these benefits can be heard