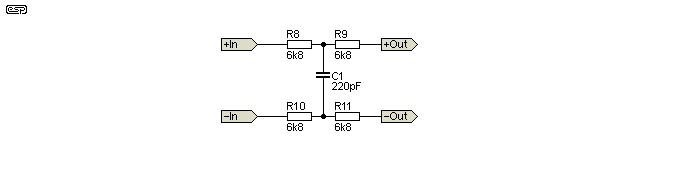
I am building a balanced-to-unbalanced receiver circuit ala ESP's Project 87 (Balanced Transmitter and Receiver II) and want to add the input filter as shown here., to trap out any RF disturbance. My question is: Does the selection of capacitor type here have any audible effect? Normally I use PolyPropylenes for any low-value capacitors in the audio path, but in this particular application, the size is quite a limiting factor; thus I am considering use of a MLCC COG type cap. Usually I would avoid any ceramics in the audio path, but in this case, is it really in the path? It would seem that the capacitor here would only be involved at super-sonic frequencies and thus a non-factor. Opinions?
I would use a low value common mode choke. No losses at all if you select the right value.
This RS PRO 100 μH 500 mA Common Mode Choke 330mΩ | RS Components will give you the idea.
This RS PRO 100 μH 500 mA Common Mode Choke 330mΩ | RS Components will give you the idea.
Unless you've already gone to far down the rabbit hole with the old, somewhat outdated Rod Elliott design, I recommend you take a good look at these THAT Corp chips:
View attachment THAT 1200-Series_Datasheet.pdf
View attachment THAT 1606-1646_Datasheet.pdf
You'll get superior performance at about the same cost, and less components to juggle too.
Mike
View attachment THAT 1200-Series_Datasheet.pdf
View attachment THAT 1606-1646_Datasheet.pdf
You'll get superior performance at about the same cost, and less components to juggle too.
Mike
This filter exclusively suppresses differential-mode noise. To remove common mode noise as well I suggest a "tapped" capacitor (2x470p) with the tap grounded.
The THAT 1200 is a fine design by Bill Whitlock of Jensen transformer fame, which is quite a credential! AND, I don't know that Rod is OUTDATED.
BUT
The LM4562 I am planning to employ has 24 db less THD, almost twice the slew rate, and less than 1/3 the cost of the THAT 1200. By hand selecting the input resistors, I believe I can achieve nearly as good a CMRR.
BUT also, I just found a PolyPro cap that IS small enough to fit! I don't know how I missed it before: WIMA FKP0D002200B00HSSD. However, it is a about 8x the cost of the MLCC COG, so...........
Last edited:
A high "Q" ceramic capacitor is called for in this application. It is the correct part and will not degrade the audio performance with any of its nonlinearities. It operates well above the audio band.
I have been looking at THAT chips like this and I have a (possibly stupid) question.
If I use one of these chips at the input in lieu of an input transformer, then will I get the same protection from ground loops? I want to use a Bluetooth board in my project, which has (of course) a single ended output.
I know that I can use an isolated power supply and avoid a ground loop. But if I stick it in an existing unit and I want to use available power, then (according to what I read from people that have used these boards) I'm stuck with a ground loop. I also know that there's a lot of Bluetooth/amplifier combo boards out there, and I wonder how they're configured to avoid this ground loop.
The solutions I've read always use a transformer. I want to avoid this for obvious reasons. Do I have to convert the signal to differential, then back to single ended, to break the loop? That's two chips. Can I do it with one chip?
Thanks.
I have been looking at THAT chips like this and I have a (possibly stupid) question.
If I use one of these chips at the input in lieu of an input transformer, then will I get the same protection from ground loops? I want to use a Bluetooth board in my project, which has (of course) a single ended output.
I know that I can use an isolated power supply and avoid a ground loop. But if I stick it in an existing unit and I want to use available power, then (according to what I read from people that have used these boards) I'm stuck with a ground loop. I also know that there's a lot of Bluetooth/amplifier combo boards out there, and I wonder how they're configured to avoid this ground loop.
The solutions I've read always use a transformer. I want to avoid this for obvious reasons. Do I have to convert the signal to differential, then back to single ended, to break the loop? That's two chips. Can I do it with one chip?
Thanks.
Rod's circuits work, and are very well sorted. I've used bits and pieces of Rod's circuits in my own builds.
NP0 / C0G capacitors are about as linear as it gets - unlike X7R, X5R, Y5V, Z5U and all the other class 2 ceramic capacitors.
Those designs deal with the problems of long balanced lines, as in studios etc. Not necessary for home systems.
In that case strict matching of R and C is required. Otherwise, part of the common mode noise will end up as differential noise.
Which approach is better ultimately depends on CMRR of the receiver and the level of CM noise.
I have a very large collection of assorted NOS high "Q" ceramic capacitors that I use for applications like this. They're like this https://www.mouser.com/ProductDetai...GAEpiMZZMuMW9TJLBQkXpKJGQ%2BaQuPsllUnV4DGgDs= but smaller.
The important parameter is the capacitor's resonance; the higher the better. Modern MLCC capacitors might be perfectly fine for this application.
How does one tell the "Q" of the various caps available? It doesn't seem to be mentioned in the datasheets I've looked at. Would a MLCC COG actually be better than a PP in this application? I was looking at these TDK FA18C0G1H221JNU00 caps:
https://www.mouser.com/ProductDetail/TDK/FA18C0G1H221JNU00/?qs=sGAEpiMZZMvsSlwiRhF8qkIxJ6vgv2FJodvgKsRQ9tvv9TF39zIteA%3D%3D
which are cheaper and smaller than the "high Q" caps you referenced.
I erred in my earlier comparison---the PP is ~ 2.5 x the cost of the MLCC COG.
https://www.mouser.com/ProductDetail/TDK/FA18C0G1H221JNU00/?qs=sGAEpiMZZMvsSlwiRhF8qkIxJ6vgv2FJodvgKsRQ9tvv9TF39zIteA%3D%3D
which are cheaper and smaller than the "high Q" caps you referenced.
I erred in my earlier comparison---the PP is ~ 2.5 x the cost of the MLCC COG.
In the old days they would specify "high Q" in the product description. In the old days there were no MLCC capacitors.
I use MLCC capacitors as local power supply bypass for op amps, per recommendation. I have also used ceramic disc capacitors for the same application with essentially the same results. The MLCC capacitors are very tiny as a bonus.
My point is that the capacitors you reference are very likely adequate for your application. Unless the circuit they're filtering has extraordinary bandwidth, it shouldn't make a difference. Old fashioned disc capacitors were used in radio equipment (a huge hobby in the 50s and 60s) at very high frequencies. They were ubiquitous back in the day, work excellent for op amp circuits, and I am likely habituated to using them. Plus, I have an enormous stash of them, NOS.
I use MLCC capacitors as local power supply bypass for op amps, per recommendation. I have also used ceramic disc capacitors for the same application with essentially the same results. The MLCC capacitors are very tiny as a bonus.
My point is that the capacitors you reference are very likely adequate for your application. Unless the circuit they're filtering has extraordinary bandwidth, it shouldn't make a difference. Old fashioned disc capacitors were used in radio equipment (a huge hobby in the 50s and 60s) at very high frequencies. They were ubiquitous back in the day, work excellent for op amp circuits, and I am likely habituated to using them. Plus, I have an enormous stash of them, NOS.
220 pF and 470 pF NP0 / C0G MLCC capacitors typically cost about $ 0.25 to $ 0.50 when bought in small quantities, that doesn't seem prohibitively expensive to me.
Regarding the need for linearity, within the passband of the filter, the voltage across the capacitor is about 71 % of the input signal voltage. For a +4 dBu sinusoidal signal, that's about 1.23 V peak, for a +14 dBu signal, about 3.9 V peak.
The capacitance of class 2 capacitors, especially small SMD types (which are good at filtering RF interference due to their small parasitic inductance), can easily change by a few percent due to such a signal level. In fact some of them are far worse than that. See Figure 1 of https://pdfserv.maximintegrated.com/en/an/TUT5527.pdf for some examples, although those are for rather larger values than are needed here.
As a rough estimate, assume that the current through the capacitor will have a harmonic distortion of the order of 0.2 %. At 10 kHz, +4 dBu, the current through the capacitor is ideally about 17 uA peak, so 34 nA peak distortion. That's equivalent to a distorting voltage of 2 times 6.8 kohm times 34 nA peak equals 462.4 uV peak across the input resistors of the filter. Compared to the assumed +4 dBu input signal, that's 0.0266 % distortion.
All in all, to save less than a dollar of money per channel, you get a roughly estimated 0.0266 % extra distortion at 10 kHz in a circuit using an extremely low distortion op-amp.
Your intent is true, but your math needs some help. 0 dbu = 0.775 volts rms. +4 dbu thus equals 1.23 volts rms, 1.74 volts peak. You cannot calculate the voltage across an element in an RC circuit by simply using the linear values; Z=√R2+1(2*π*f*C)2 is the appropriate formula, thus giving ~73.6K ohms of impedance at 10 KHz loading the 1.74 peak voltage; 23.6uA peak current.
Last edited:
I assume that the right hand side of the schematic of post #1 is to be loaded by two times 10 kohm to (virtual) ground, per the Balanced Transmitter and Receiver II you referred to. For frequencies far below cut-off, you then get a simple resistive voltage division in each branch between 6.8 kohm and 6.8 kohm + 10 kohm. As 16.8/(16.8 + 6.8) ~= 0.71, the voltage across the capacitor is about 71 % of the input voltage. At higher frequencies, the voltage gets smaller due to the filtering effect of the capacitor.
71 % of 1.74 V divided by 1/(2 pi f C) is about 17 uA peak when f = 10 kHz and C = 220 pF.
71 % of 1.74 V divided by 1/(2 pi f C) is about 17 uA peak when f = 10 kHz and C = 220 pF.