First I apologize as I am sure this question has been asked and answered, I simply cannot find it anywhere (Probably am not constructing the correct search string).
I am designing cabinet for a FRFR guitar speaker. My question relates to the port tube.
With Thiele / Small the volume of free air within the cabinet seems to be crucial.
The walls of the port tube do indeed take up volume within the cabinet.
Question: Does one subtract the volume introduced by the walls of the portion of the port tube that is sticking into the internal area of the cabinet from the internal volume of the cabinet?
I hope I am making myself clear.
Volume of a cylinder: Volume=(Pi*Radius^2*Length);
Where:
- Radius^2 means Radius Squared.
- Length is the length of the port tube that is sticking into the cabinet.
So the internal volume of the cabinet consumed by the port tube walls is:
(Pi*((OD/2)^2)*Length)-(Pi*((ID/2)^2)*Length).
Note: My port tube is straight on both ends (no flanges).
If one wants to reply with something like 'It is negligible, don't worry about it' save your time as I am an extremely anal individual! 🙂
Thanks for any assistance.
I am designing cabinet for a FRFR guitar speaker. My question relates to the port tube.
With Thiele / Small the volume of free air within the cabinet seems to be crucial.
The walls of the port tube do indeed take up volume within the cabinet.
Question: Does one subtract the volume introduced by the walls of the portion of the port tube that is sticking into the internal area of the cabinet from the internal volume of the cabinet?
I hope I am making myself clear.
Volume of a cylinder: Volume=(Pi*Radius^2*Length);
Where:
- Radius^2 means Radius Squared.
- Length is the length of the port tube that is sticking into the cabinet.
So the internal volume of the cabinet consumed by the port tube walls is:
(Pi*((OD/2)^2)*Length)-(Pi*((ID/2)^2)*Length).
Note: My port tube is straight on both ends (no flanges).
If one wants to reply with something like 'It is negligible, don't worry about it' save your time as I am an extremely anal individual! 🙂
Thanks for any assistance.
This might or might not help -
How Good Is Your Port | audioXpress
I actually admire somebody who is correctly designing a loudspeaker cabinet especially a ported one , its not easy .
I am very naive to comments as regards "anal " and had to look it up I hope my blocking of tracking is good as some of the results would make me look in a bad light but luckily I don't use Google anything and I found the right answer ( among many I would certainly not post ! ).
Nothing wrong with an extreme attention to detail without it technical progress would be limited.
How Good Is Your Port | audioXpress
I actually admire somebody who is correctly designing a loudspeaker cabinet especially a ported one , its not easy .
I am very naive to comments as regards "anal " and had to look it up I hope my blocking of tracking is good as some of the results would make me look in a bad light but luckily I don't use Google anything and I found the right answer ( among many I would certainly not post ! ).
Nothing wrong with an extreme attention to detail without it technical progress would be limited.
Thanks Duncan2, Gala.
Gala, not that I do not trust you, but where did you source your answer from?
I am looking for a real good source on Thiele / Small.
Thank you.
Gala, not that I do not trust you, but where did you source your answer from?
I am looking for a real good source on Thiele / Small.
Thank you.
The duct walls are generally insignificant.
But look at the basic tuned system. A volume of air, and a duct.
The duct could be outside the box. If you "hide" it inside, then the box must be that much bigger, the total volume of the duct. (+/- end-effects but I'll leave that to the truly obsessed.)
Note that "flat" loses meaning on a self-played instrument. If say 87Hz is up a dB, the skilled player will pluck just that much less. Unlike HiFi where the balance is carved in vinyl and not easily adjusted by the user.
But look at the basic tuned system. A volume of air, and a duct.
The duct could be outside the box. If you "hide" it inside, then the box must be that much bigger, the total volume of the duct. (+/- end-effects but I'll leave that to the truly obsessed.)
Note that "flat" loses meaning on a self-played instrument. If say 87Hz is up a dB, the skilled player will pluck just that much less. Unlike HiFi where the balance is carved in vinyl and not easily adjusted by the user.
rMidi,
The air in the port is incompressible (no change in velocity across the port), and thus provides no addition to the compliance of the air in the box- it shouldn't be counted as useable volume.
You must not be too anal. It's Galu, not Gala 😀
Thanks PRR.
I do understand what you are saying.
In the FRFR (Flat Range, Falt Response) this really is not about dB's. Its about reproducing a signal without any colorization from the speaker(s) or cabinet.
So far from my short excursion into the Thiele / Small cabinet design world I have found that a significant number of the sources on the net do not seem to be very reliable as far as the information they are presenting. All of the 'calculator' sites simply seem to be 100% incorrect in their calculations.
For instance mh-audio.nl has a calculator to calculate port length (amongst many). It asks for the 'volume of box'. I am assuming the volume asked for must be the net volume, not the gross volume. Since Gula pointed out that the portion of the port tube extending into the cabinet fills up more of the interior volume (reducing the net volume) how could one possibly know the 'volume of box' without already knowing the length of the port tube? What is the purpose of such a calculator? Am I missing something here?
Sigh, I am at a loss.😕
I do understand what you are saying.
In the FRFR (Flat Range, Falt Response) this really is not about dB's. Its about reproducing a signal without any colorization from the speaker(s) or cabinet.
So far from my short excursion into the Thiele / Small cabinet design world I have found that a significant number of the sources on the net do not seem to be very reliable as far as the information they are presenting. All of the 'calculator' sites simply seem to be 100% incorrect in their calculations.
For instance mh-audio.nl has a calculator to calculate port length (amongst many). It asks for the 'volume of box'. I am assuming the volume asked for must be the net volume, not the gross volume. Since Gula pointed out that the portion of the port tube extending into the cabinet fills up more of the interior volume (reducing the net volume) how could one possibly know the 'volume of box' without already knowing the length of the port tube? What is the purpose of such a calculator? Am I missing something here?
Sigh, I am at a loss.😕
Gads!
I cannot believe I misspelled 'Galu' twice!
I will flog myself a sufficient number of times this evening until I get over it!
tsmith (yes I have shortened you handle, dropped off he 1315 to save time. Did I save time? No because I have spent 'saved' time explaining it 10 fold)
Thanks for the explanation. Aha! Of course the air within the port tube cannot be compressed! It acts like a piston then does it not?
I cannot believe I misspelled 'Galu' twice!
I will flog myself a sufficient number of times this evening until I get over it!
tsmith (yes I have shortened you handle, dropped off he 1315 to save time. Did I save time? No because I have spent 'saved' time explaining it 10 fold)
Thanks for the explanation. Aha! Of course the air within the port tube cannot be compressed! It acts like a piston then does it not?
Are you using their 'new' calculator? HiFi Loudspeaker Design
It accepts the T/S parameters and port diameter to calculate the box volume for a flat amplitude response. It also allows customisation of the box volume.
Vb in this calculator is "The airspace volume of the box. The volume of the driver and any building material needs to be added to this value."
Since the port takes up airspace in the box do we similarly add its volume to Vb?
You are correct in that the calculator does not specifically say that you should do so and, like you, I would welcome further comment.
The majority of speaker designers on this forum use computer software which must obviate the problem.
Thanks Galu.
No I was not using the 'new' calculator. Thanks for the link. I will take a look.
I have been thinking about the port taking up air space.
My question:
Does the port tube act the same is it is extending outside of the cabinet rather than into the cabinet?
New terms I believe I am using correctly:
- Gross volume. The internal volume of the cabinet excluding all other things (driver mass, building materials, port tube,..)
- Net volume. Gross volume minus all things taking up volume within the cabinet (driver mass, building material, port tube,..)
Perhaps this is true?
-- The port extends into the box and takes up air space, decreasing the net volume.
-- DOES A PORT WORK THE SAME WAY IF IT IS EXTENDING OUTSIDE OF THE CABINET?
-- If the above is true (Feel free to tell me if I am correct or not) then:
---- Calculate the length of the port tube utilizing the existing net volume (does not include port tube volume)
---- Now I have the port tube length.
---- Increase the internal 'gross' (non net, not including volume of driver, building materials,....) by the volume that would be taken up by the ort tube extending into the cabinet.
---- Muck with the dimensions of the cabinet to accommodate for the new 'gross' volume.
Thanks for all of your help so far.
No I was not using the 'new' calculator. Thanks for the link. I will take a look.
I have been thinking about the port taking up air space.
My question:
Does the port tube act the same is it is extending outside of the cabinet rather than into the cabinet?
New terms I believe I am using correctly:
- Gross volume. The internal volume of the cabinet excluding all other things (driver mass, building materials, port tube,..)
- Net volume. Gross volume minus all things taking up volume within the cabinet (driver mass, building material, port tube,..)
Perhaps this is true?
-- The port extends into the box and takes up air space, decreasing the net volume.
-- DOES A PORT WORK THE SAME WAY IF IT IS EXTENDING OUTSIDE OF THE CABINET?
-- If the above is true (Feel free to tell me if I am correct or not) then:
---- Calculate the length of the port tube utilizing the existing net volume (does not include port tube volume)
---- Now I have the port tube length.
---- Increase the internal 'gross' (non net, not including volume of driver, building materials,....) by the volume that would be taken up by the ort tube extending into the cabinet.
---- Muck with the dimensions of the cabinet to accommodate for the new 'gross' volume.
Thanks for all of your help so far.
If it's just a case of understanding loudspeaker data, then Eminence give good support: Understanding Loudspeaker Data | Eminence Speaker
By the way, things like this are very confusing to me.
I assume that all things 'port tube' are interacting with the free air space within the cabinet. Am I correct here?
I refer to the free air space as the net volume.
I assume that Vb is the 'Gross' volume of the cabinet. So shouldn't this be 'needs to be subtracted from this value'?
(Gross Volume - (driver mass + building materials))= Net volume.
I would think that the length of the port tube is in relation to the current net volume.
I assume that all things 'port tube' are interacting with the free air space within the cabinet. Am I correct here?
I refer to the free air space as the net volume.
I assume that Vb is the 'Gross' volume of the cabinet. So shouldn't this be 'needs to be subtracted from this value'?
(Gross Volume - (driver mass + building materials))= Net volume.
I would think that the length of the port tube is in relation to the current net volume.
The port works the same way whether it is located inside the cabinet, outside, or some of both.
As for Vb:
Consider this formula (Keele?) for calculating a vented Vb from T/S parameters:
Vb = 15 Vas (Qts ^ 2.87)
It becomes obvious that Vb is the net amount of usable air inside the enclosure. Like Vas and Qts, Vb has a specific meaning in speaker building.
1) If you start out by defining a target Vb based on driver parameters- once you have calculated that target, add volume to compensate for what's lost when braces and baskets, etc are placed into the enclosure. Call that new, larger estimated volume before adding braces whatever you want, it's no longer Vb.
2) If you are working backwards from a user-defined volume as a design constraint, then you will have to estimate how much of that space will be rendered unusable, subtract it and what you have left is the Vb. Yes, in this case determining Vb for a vented design is an iterative process because port dimensions and Vb are intertwined.
BUT, it's easy to over-analyze and nitpick details that are not too significant in the end.
For example: If you're basing your build on published specs, be aware that it's not uncommon for them to be off 10 or 20%, even more. Think about how accurate you really need to be in that case.
As for Vb:
Consider this formula (Keele?) for calculating a vented Vb from T/S parameters:
Vb = 15 Vas (Qts ^ 2.87)
It becomes obvious that Vb is the net amount of usable air inside the enclosure. Like Vas and Qts, Vb has a specific meaning in speaker building.
1) If you start out by defining a target Vb based on driver parameters- once you have calculated that target, add volume to compensate for what's lost when braces and baskets, etc are placed into the enclosure. Call that new, larger estimated volume before adding braces whatever you want, it's no longer Vb.
2) If you are working backwards from a user-defined volume as a design constraint, then you will have to estimate how much of that space will be rendered unusable, subtract it and what you have left is the Vb. Yes, in this case determining Vb for a vented design is an iterative process because port dimensions and Vb are intertwined.
BUT, it's easy to over-analyze and nitpick details that are not too significant in the end.
For example: If you're basing your build on published specs, be aware that it's not uncommon for them to be off 10 or 20%, even more. Think about how accurate you really need to be in that case.
Tim is on the ball here. 😎 I'm just an old school, back of the cigarette pack, designer!
Just another wee comment on accuracy:
Thiele's data is based on pure theory, but your system may have losses that prevent agreement between predicted response and measured performance.
Small actually specified that about 30% overvolume was necessary to make up for typical losses.
Fine tuning can always be done by adjusting the length of the reflex tube. You may not end up with a system that is theoretically perfect, but it's more important that you get it to sound right for your guitar reproduction purposes.
Just another wee comment on accuracy:
Thiele's data is based on pure theory, but your system may have losses that prevent agreement between predicted response and measured performance.
Small actually specified that about 30% overvolume was necessary to make up for typical losses.
Fine tuning can always be done by adjusting the length of the reflex tube. You may not end up with a system that is theoretically perfect, but it's more important that you get it to sound right for your guitar reproduction purposes.
Tim Said:
'Consider this formula (Keele?) for calculating a vented Vb from T/S parameters:
Vb = 15 Vas (Qts ^ 2.87)
'
I see this same formula on pages such as DiyAudioCorner:UsefulFormulas.
I also see form the above link that this is in ft3.
With this said I assume that:
- The value for Qts is to be given in ft3 for the calculation.
- The output of the calculation is in ft3.
Being the newbee that I am I read this as utilizing the following operators:
Vb=(15 x Vas x (Qts^2.87))
This cannot be right, can it?
Published Celestion specifications for F12-FX200:
Vas: 47.3Liters / 16.7ft3
Qts: 0.777
Vb=(15 x 16.7 x (Qts^2.87))
Vb=((250.5) x (0.4847394033527477093283460679479))
Vb=121.42722053986330118675069002095
I am assuming that 121.42722053986330118675069002095 is in ft3.
Wouldn't this be cabinet that is roughly 5' x 5' x 4.86'?
Perhaps this is correct and this has something to do with it:
- Celestion F12-FX200 1x12 Cabinet Design. The PDF is downloadable from this page.
- I Asked Dr. Decibal (whomever He or She is) about the lining of the cabinet with polyester wadding that is called for in the design.
-- Let me apologize for only including He and She as genders and do not want to alienate anyone here. I understand the ABC news has identified 58 gender options but it is not practical to include all 58 of the in this post
- Dr. Decibal responded with 'It fools the speaker into thinking it is living in a larger cabinet'.
Note: I do understand that the Celestion design is not perfect.
I am starting to think that this speaker / cabinet / box / tuning world is actually no place for an anal programmer such as myself!
Cheers
'Consider this formula (Keele?) for calculating a vented Vb from T/S parameters:
Vb = 15 Vas (Qts ^ 2.87)
'
I see this same formula on pages such as DiyAudioCorner:UsefulFormulas.
I also see form the above link that this is in ft3.
With this said I assume that:
- The value for Qts is to be given in ft3 for the calculation.
- The output of the calculation is in ft3.
Being the newbee that I am I read this as utilizing the following operators:
Vb=(15 x Vas x (Qts^2.87))
This cannot be right, can it?
Published Celestion specifications for F12-FX200:
Vas: 47.3Liters / 16.7ft3
Qts: 0.777
Vb=(15 x 16.7 x (Qts^2.87))
Vb=((250.5) x (0.4847394033527477093283460679479))
Vb=121.42722053986330118675069002095
I am assuming that 121.42722053986330118675069002095 is in ft3.
Wouldn't this be cabinet that is roughly 5' x 5' x 4.86'?
Perhaps this is correct and this has something to do with it:
- Celestion F12-FX200 1x12 Cabinet Design. The PDF is downloadable from this page.
- I Asked Dr. Decibal (whomever He or She is) about the lining of the cabinet with polyester wadding that is called for in the design.
-- Let me apologize for only including He and She as genders and do not want to alienate anyone here. I understand the ABC news has identified 58 gender options but it is not practical to include all 58 of the in this post
- Dr. Decibal responded with 'It fools the speaker into thinking it is living in a larger cabinet'.
Note: I do understand that the Celestion design is not perfect.
I am starting to think that this speaker / cabinet / box / tuning world is actually no place for an anal programmer such as myself!
Cheers
There are no units for Qts, the resulting Vb will be in whatever units you use for your Vas.
BTW, that is by no means the only valid method of determining a Vb. Instead of using a formula, most people these days seem to just start with a sim using recommended values, and fiddle around from there.
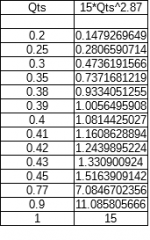
In that formula, the term 15(Qts^2.87) is a multiplier. Consider it a function of Qts that relates Vb to Vas.
Calculating that multiplier for some various values of Qts in the chart below, you see that somewhere around 0.4, the Vb needed for this alignment is about equal to Vas.
Lower Qts values need volumes lower than Vas, and higher Qts values need volumes larger than Vas. Again, this isn't the only valid path to determine a Vb. But that general trend for Vb vs Qts holds true if your goal is keeping a relatively flat response.
This is pretty much jumping in the middle of the subject, and not a good place to start.
BTW, that is by no means the only valid method of determining a Vb. Instead of using a formula, most people these days seem to just start with a sim using recommended values, and fiddle around from there.
In that formula, the term 15(Qts^2.87) is a multiplier. Consider it a function of Qts that relates Vb to Vas.
Calculating that multiplier for some various values of Qts in the chart below, you see that somewhere around 0.4, the Vb needed for this alignment is about equal to Vas.
Lower Qts values need volumes lower than Vas, and higher Qts values need volumes larger than Vas. Again, this isn't the only valid path to determine a Vb. But that general trend for Vb vs Qts holds true if your goal is keeping a relatively flat response.
This is pretty much jumping in the middle of the subject, and not a good place to start.
Attachments
Last edited:
Don't worry Galu, I won't make a habit of it! Heading back to the peanut gallery now...
