No, of course not ..it's obviously the pict of the wav file i uploaded
The listening test was pretty darn conclusive.
But I'll probably still do the mic & scope test,
as much to learn how to do the necessary scope triggering, as to see how the measurement compares to the wave.
But learning that triggering may come easy or hard, sooner or later...dunno...current project..
Will post scope trace if i get it to work well.... when i feel it's real data...
The listening test was pretty darn conclusive.
But I'll probably still do the mic & scope test,
as much to learn how to do the necessary scope triggering, as to see how the measurement compares to the wave.
But learning that triggering may come easy or hard, sooner or later...dunno...current project..
Will post scope trace if i get it to work well.... when i feel it's real data...
No, of course not ..it's obviously the pict of the wav file i uploaded
The listening test was pretty darn conclusive.
Of what? Now listen to it thru a full range speaker. Notice any difference?
Look at the end of the sine where it does an instant 45 degree change. The speaker cone has to stop instantly. And start instantly at the begining. This is only possible with infinite bandwidth. Thats why these waveforms do not exist in nature.
Last edited:
Hi cbdb,
Yes, when i listen to it full range it gets sharper, more full spectrum.
But I'm a little suspect about the test file now...
JRiver buffers and plays it quite differently, play to play.
Didn't hear that with just the sub.
Maybe it's just too short a file to use..
I'd advise folks not to try it with anything other than a sub, or better just scrap it, till a proven file that has digital silence before and after to make sure it plays correctly.
I'm out of my element building digital soundtracks....looking forward to trying my arb generator output, when the amplifier option arrives.
When you explain why these waveforms do not exist in nature, that makes sense.
Thx ! 🙂
Yes, when i listen to it full range it gets sharper, more full spectrum.
But I'm a little suspect about the test file now...
JRiver buffers and plays it quite differently, play to play.
Didn't hear that with just the sub.
Maybe it's just too short a file to use..
I'd advise folks not to try it with anything other than a sub, or better just scrap it, till a proven file that has digital silence before and after to make sure it plays correctly.
I'm out of my element building digital soundtracks....looking forward to trying my arb generator output, when the amplifier option arrives.
When you explain why these waveforms do not exist in nature, that makes sense.
Thx ! 🙂
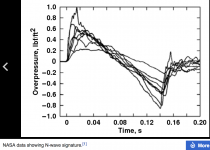
The naturally occurring "N" waveform of a thunderclap would have some similarity to a truncated sine wave like Mark posted.Thats why these waveforms do not exist in nature.
Although I have heard the "crack" sound of randomly truncated sine waves many times when un-muting them through a good full range system, having been within 100 feet of a lightning strike two times in my life, have to say there is no sound system that has come very close to reproducing that sound.
And that's fine by me- but still wonder what the OP Wonderfulaudio application is...
Art
Attachments
Last edited:
You wouldn't, obviously, can't you use REW to measure the subs output?Didn't hear that with just the sub.
.. but still wonder what the OP Wonderfulaudio application is...
Me, too. I've kept reading, hoping he'd pop back in -- and explain ..
Wow, Art -- twice within 100 feet -- bet that raised your blood pressure!
I think I see the light bulb coming on for mark100 -- let's see those recorded waveforms.
Cheers
Yeplet's see those recorded waveforms.
You seemed so eager 🙂I just can't buy that a 50Hz sine wave needs full spectrum bandwidth to be faithfully reproduced till i see, hear, and measure it ....
BTW, recording means, er, recording, not something made in a file 🙄
If I have understood correctly, the thesis is that a single sine wave is not actually a sine wave at all. This is because, for example, when it starts at t=0, it needs to accelerate from a velocity of zero to a finite velocity in zero time; this is infinite acceleration and it is posited that this requires an infinitely large bandwidth. A continuous sinewave, on the other hand, has the advantage of momentum to help the system achieve the velocity required at the zero crossing.
This sounds believable as a thought experiment, but if the reasoning is correct, then surely we would expect the fft of a “single sinewave cycle that is not really a sinewave at all” to show a raft of harmonics, which would be the reason it would require a large bandwidth. If the harmonics are not there, then there would be no need for the large bandwidth.
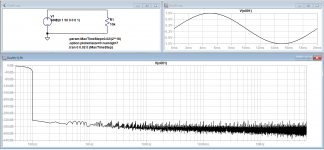
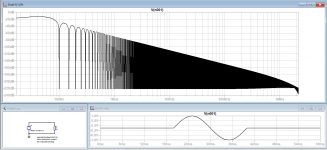
LTspice will happily perform an fft on one cycle of a 50Hz sinewave. I’ve attached a screenshot below. I can’t see any evidence of this requiring a large bandwidth. Moreover, if the output is filtered at, say, 100Hz, the single sinewave cycle will still be passed unchanged.
Since the time-domain and frequency-domain analyses are mathematically related and just different views of the same phenomena, perhaps someone here could explain to me how this relationship is apparently broken in the case of a single sinewave cycle.
This sounds believable as a thought experiment, but if the reasoning is correct, then surely we would expect the fft of a “single sinewave cycle that is not really a sinewave at all” to show a raft of harmonics, which would be the reason it would require a large bandwidth. If the harmonics are not there, then there would be no need for the large bandwidth.
LTspice will happily perform an fft on one cycle of a 50Hz sinewave. I’ve attached a screenshot below. I can’t see any evidence of this requiring a large bandwidth. Moreover, if the output is filtered at, say, 100Hz, the single sinewave cycle will still be passed unchanged.
Since the time-domain and frequency-domain analyses are mathematically related and just different views of the same phenomena, perhaps someone here could explain to me how this relationship is apparently broken in the case of a single sinewave cycle.
Attachments
As a matter of interest, what does it make of the signal if you have a period of time at 0V before and after the wave?
Good question.
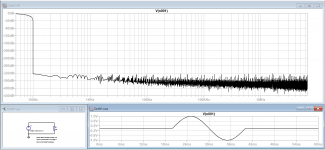
Capture1.png is the fft over the time period of the single cycle only.
Capture2.png is the fft over the whole of the time period, i.e. with silence before and after included in the fft.
Not quite sure what to make of that!
Capture1.png is the fft over the time period of the single cycle only.
Capture2.png is the fft over the whole of the time period, i.e. with silence before and after included in the fft.
Not quite sure what to make of that!
Attachments
Attachments
- Home
- Loudspeakers
- Subwoofers
- Achieve good time domain behaviour to produce single cycle sine