So all pass filters and LR4 crossovers are both evil and objectionable?
Not solely on the basis of principle, IMHO. "How does it sound?" is always a question, along with, "how do you like it?"
The dilemma of WHY loudspeakers seem to get away with so much distortion and phase shift is a real one. In fact, it drove a wedge between my professional relationship of John Meyer and myself, some 40+ years ago. Back then we had a lab together, making a world class all horn loaded PA loudspeaker. We acquired one of the first FFT systems, for about $50,000 (big bucks at the time) from Tektronix and we made all kinds of measurements, mostly speaker measurements, of course. Well, when it came to my electronic gain modules, a 10bit FFT measurement hardly could find anything thing at all, and this extended to some IC's as well. At this point John Meyer decided that audio electronics was easy, and I was replaceable. After all, speakers had so many more problems, didn't they? Of course, I mustered on, subjectively trying the 5534, for example when it first came out. Yet, I found that quality discrete was still better sounding than the 5534, etc at the time (40 years ago) so I had to keep making discrete op amps, etc, (darn, it would have saved me a lot of time and money to just use IC's), but if I wanted to make something special, I had to do it with discrete components for the most part. I made a few studio boards, and analog tape recorders back then with discrete 'op amp' cards, and even simpler Trans-amps that I put in, where I could get away with not having a buffered output stage. Even today, I would have to design a discrete op amp, instead of using IC's, and important exception might be the AD-825, or some current mode IC's that I don't normally have available.
Last edited:
Do they? Is it? People talk a lot about the differences in the sound of speakers.The dilemma of WHY loudspeakers seem to get away with so much distortion and phase shift is a real one.
I agree on the first sentence. We still have a LOT to discover on how our brains are processing the sounds.The dilemma of WHY loudspeakers seem to get away with so much distortion and phase shift is a real one...
... Even today, I would have to design a discrete op amp, instead of using IC's, and important exception might be the AD-825, or some current mode IC's that I don't normally have available.
For the second sentence, I'm pretty happy with some FAST OPAs. Adding buffers when they are used in line output stages.
BTW: Like you, I really dislike 2N5532 too.
I agree with SJ... it's not a dilemma, it's well known and observed, and much harder to deal with than the electronics, which is pretty easy now. LS distortion is often quite audible.
I agree on the first sentence. We still have a LOT to discover on how our brains are processing the sounds.
For the second sentence, I'm pretty happy with some FAST OPAs. Adding buffers when they are used in line output stages.
BTW: Like you, I really dislike 2N5532 too.
Try the https://wakamatsu.co.jp/waka/snas386f-317462.pdf
🙂
THx-RNMarsh
Last edited:
Tried, loved 🙂
One of the very few that are optimized with a feedback resistance between 1 & 2 kOhms. Well done !
Last edited:
It isn't phase shift (time domain waveform distortion) per se that matters so much to humans (except maybe at LF and for the punch of percussive sounds which tend to be heard more according to their time domain waveforms), as much as it is rate of change of phase with respect to frequency, aka Group Delay, IMHO.
Mark,
That makes sense, if harmonics of a particular fundamental are delayed with respect to that fundamental, a change in timbre could possibly be heard. This being said, I have read studies over the years flatly stating group delay cannot be heard without qualification, which doesn't make sense to me.
Audibility of group delay should be proportional to what frequency it starts at (filter corner freq?) and how much delay is caused (filter order?). Perhaps there is a minimum amount which is perceived? And what is the group delay worst case of common DAC filters..and at what frequency?
All of which I donna know...
Cheers!
Howie
Audibility of group delay should be proportional to what frequency it starts
at (filter corner freq?) and how much delay is caused (filter order?).
Nonlinear phase shift in a first order low pass filter begins at around
1/10 of the corner frequency, and follows an arctangent function.
Here's an example of (normalized) filter delay. The first order delay
is 1/BW, where the BW is in radians/second. Higher order filters have
increasing delay, as shown here. The Bessel is the best type in this respect.
Attachments
Last edited:
And what is the group delay worst case of common DAC filters..and at what frequency?
IMHO, with purely linear phase interpolation I wouldn't expect audible group delay, however there is an IIR filter the runs after the interpolation filter. Apparently, the IIR filter is what determines the fast or slow transition property of the selectable built-in interpolation filters. I suspect that is the case because I believe that even if custom interpolation filter coefficients are loaded and selected in the dac, it is still possible to choose one of the built-in filters to give the custom filter a slow-transition property in addition to (or modifying) its own frequency contour.
It may be that if using a linear phase interpolation filtering, the problem is not group delay in this particular case. Rather is may be there are just not enough taps available to attenuate the transition band fast enough and the stop band deep enough to keep all aliasing inaudible. Again, that is an inference from something about the dac which is that the PRO chips can be run in stereo only mode all 8 dac channels either used for one stereo channel or the other, either that or any channels not used for stereo may be left unused. Reason is because in stereo only mode the built-in interpolation filter taps can be doubled from 128 to 256 taps (which requires loading custom coefficients). That leaves not enough extra taps and DSP configurability for any more than 2 interpolated channels, but the filter could then be made faster and deeper. Why? My guess would be that if all the dac channels are used to make two stereo channels, noise can be reduced by combining all the analog outputs into 2 channels. In that case dynamic range can be enough so that noise does not sufficiently mask remaining aliasing if using only 128 filter taps. Again, a guess. Don't know why else that feature may be there. Well, if only a bit of noise is masking aliasing according to someone's reckoning, maybe it isn't quite masked enough for someone else's brain processing. That's all.
Last edited:
Nonlinear phase shift in a first order low pass filter begins at around
1/10 of the corner frequency, and follows an arctangent function.
Here's an example of (normalized) filter delay. The first order delay
is 1/BW, where the BW is in radians/second. Higher order filters have
increasing delay, as shown here. The Bessel is the best type in this respect.
Are you saying this delay as opposed to phase shift?
Are you saying this delay as opposed to phase shift?
The time delay (as a function of frequency) is the derivative of the phase shift, d(phase)/df.
If the phase is a linear function of frequency, then the time delay is a constant for all frequencies,
and the input signal wave shape is preserved, though delayed.
If the phase (as a function of frequency) = K*f, where K is a constant,
then the time delay is d(K*f)/df = K * df/df = K, a constant independent of frequency.
So the time delay is the same for all frequencies, and the input waveform is preserved.
The value of K (the delay) will vary with the type and order of filter.
Attachments
Last edited:
I wasn't aware that Black treated a non-linear transfer function in detail at all, in that sense one might say "approximation". I would call that a somewhat poor choice of words.
The problem has a solution, http://www.its.caltech.edu/~musiclab/feedback-paper-acrobat.pdf
Thanks very much for your help. I'd seen the Boyk paper before, but put in a better effort this time, with a somewhat better result. For me, it's still a distance between that level of maths and an intuitive knowledge; more like translating from a non-Romance language to English. And it seems there's no understanding this without penetrating the maths.
Again, much thanks,
Chris
The new terms (re-entrant distortion) do not appear because the signal has gone round the loop again. They appear as an unavoidable matter of algebra and so can appear even in the ideal case of instantaneous signal propagation. The feedback is trying to adjust the input seen by the amplifier (the 'error' signal in servo terms) so that the output follows the signal input; anything in the output which is not in the input is attenuated. Essentially the feedback is doing an inversion.
To give a simple example, assume the amp output is 1+x - where x is something not in the input. To correct this the feedback has to generate 1/(1+x).
1/(1+x) = 1 -x +x^2 -x^3 +x^4 etc.
Can you see how simple algebra generates re-entrant distortion even when everything happens simultaneously?
That is all amazingly clear. Thank you very much. You're a great teacher, the highest calling.
An important part that I still don't understand is why the feedback generates the reciprocal of the output. It seems to come from Black, and you're showing me a simple enough version for my limitations. I'll need to work on this quite a lot more, but you've gotten me to place where I can see the mountaintop and with renewed hope of reaching it.
Again my deep thanks,
Chris
Yes, It is the time the sounds that come from our speakers takes to reach our ears. Each frequency with the same delay. It is important for the speakers that compose our sets to be "time aligned" (their distances) if we want square waves to be properly reproduced.If the phase is a linear function of frequency, then the time delay is a constant for all frequencies, and the input signal wave shape is preserved, though delayed.
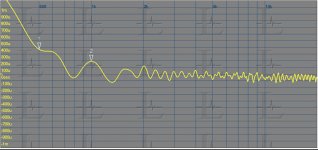
Mr Leon, the creator of Elipson, used to do this in the 70th. Because the wave lengths are short at high frequencies, it is more critical as the cross frequency increases (medium/treble).(See attached 1)
A simple way to tune-it is to optimize square waves. Or/and, for those who use DSP active filters with adjustable delays, to tune it carefully.(see attached 2 & 3)
Attachments
Last edited:
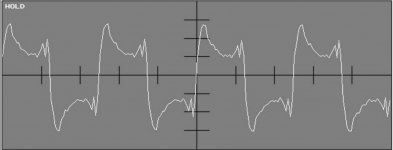
Phase issues can cause peak amplitude issues.Allpass.pdfDan.
Thanks Max, that is one type of phase modification I have experience with, in the broadcast industry we sometimes call that phase scrambling. Early all-pass scramblers and clippers produced audible artifacts as well as sometimes causing early FM transmitters to lose PLL lock due to LF (<1 Hz) energy causing center frequency offsets. Later units performed composite (combined L+R baseband and L-R subcarrier) signal processing for maximum loudness (a policy I abhor) without over-modulating or losing transmitter frequency lock.
I have done many hours of comparisons pre/post processing, listening to processors both at home and in studios auditioning them pre-purchase, and the early units including even the vaunted Orban 8000A (early 1980s) can cloud and smear CD-quality material, especially that with with significant HF energy. This full-time allpass approach is what made me disagree with the statement that phase delay is inaudible.
The algorithms used in the modern DSP-based audio processors/stereo generators such as the Orban 8500 (2000's) and newer are able to selectively alter phase of asymmetrical signals only when needed with extremely few if any audible side-effects. Analysis of crest factor before and after processing shows little if any difference if the processing is set up merely for peak AGC. Progress indeed, with kudos to Bob Orban and Greg Ogonowski...
Howie
You're welcome, and audibility is why I brought it up in the middle of the current claims counter to this.Thanks Max, that is one type of phase modification I have experience with, in the broadcast industry we sometimes call that phase scrambling.......This full-time allpass approach is what made me disagree with the statement that phase delay is inaudible.
There are VST etc plugins to do such processing, it would be educational for most to do some AB comparisons.
Subtle frequency dependent phase shifting can cause increase or decrease in peak values, and this may trigger changes in system behaviours that are directly audible.
'Theory' says levels of harmonics are the same and that area under curves are the same....so they must sound the same !.
Changes in timings of harmonics registers in the brain as a change in conditions and is an alert signal.....something wrong if we did not pick it up.
Dan.
Last edited:
- Status
- Not open for further replies.
- Home
- Member Areas
- The Lounge
- John Curl's Blowtorch preamplifier part III