Zobel

Status
Not open for further replies.
Jump to Latest
#2
Re

But, I can usually do a little better using XSim and tweaking it. 🙂

Also, bumping the values of the Zobel you can sometimes nudge the driver phase a little, helping with driver matching.

So use the calculators only as a starting point.

Best,

E
 
#7
Ah, the inevitable re-appearance of that piece of nonsense formula for speaker impedance correction, falsely attributed to Zobel. The correct method to obtain a flat impedance with minimum phase i.e. the speaker will look like a resistance in the crossover frequency range is to use Boucherot's method for power factor correction. This involves finding the impedance and phase of the speaker at the crossover frequency and solving for R=cos theta.Z and for XL= sin theta.Z From this information vector formula methods are used to resolve the distribution of current in the correction circuit to find the values for C and R. The Smith & Larson Woofer Tester will do all this for you, if you are not familiar with the maths involved.
 
#8
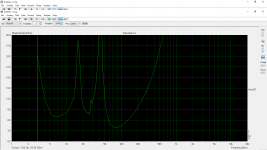
Without zobel

An externally hosted image should be here but it was not working when we last tested it.


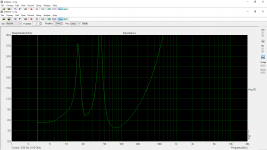
With zobel as per calculator 12.2uF + 7 ohms (using Re)

An externally hosted image should be here but it was not working when we last tested it.


With zobel 9uF + 8,2 ohms (using nominal driver impedance not Re)

An externally hosted image should be here but it was not working when we last tested it.
 
Last edited:
#11
Because 12uF has a reactive impedance of ~26ohms at 500Hz, just like what your plot is showing.

You need a capacitor that has a low impedance at the higher frequency so that the source sees the added R as a load in parallel to the voice coil.

Effective impedance = sqrt (26.5^2 + 7^2) =~27ohms.
 
Last edited:
#12
75uF + 8R2
 

Attachments

  • limp 9m + seteta tresuF co zobel seteta cico uF 8R2.png
    limp 9m + seteta tresuF co zobel seteta cico uF 8R2.png
    22.4 KB · Views: 211
#14
Thanks Andrew now I understand how it's work.

AndrewT said:
Because 12uF has a reactive impedance of ~26ohms at 500Hz, just like what your plot is showing. please show me the maths to calculate by myself

You need a capacitor that has a low impedance at the higher frequency so that the source sees the added R as a load in parallel to the voice coil.

Effective impedance = sqrt (26.5^2 + 7^2) =~27ohms. what's 26.5 & 7?
Click to expand...
 
#17
AndrewT said:
Because 12uF has a reactive impedance of ~26ohms at 500Hz, just like what your plot is showing.

You need a capacitor that has a low impedance at the higher frequency so that the source sees the added R as a load in parallel to the voice coil.

Effective impedance = sqrt (26.5^2 + 7^2) =~27ohms.
Click to expand...

merlin el mago said:
Thanks Andrew now I understand how it's work.
Click to expand...
Frequency F0 =1/{2PiXcC} for capacitor and F0 = XL/{2PiL}
XL= 2*Pi*F0*L
This is 90degrees phase difference to the resistor's impedance.
You add these two 90degrees phase difference impedances using the sqrt of squares rule
Effective impedance = Sqrt( XL^2 + R^2)
 
#20
Hi merlin el mago,

Before you run an impedance test in Limp, make sure you run a calibration test via the CAL button.
After that, measure the impedance of a resistor (for example 8.2 ohms metal film or metal oxide). If the response (in ohms and phase) is nice and flat, you can then be assured that your loudspeaker impedance measurements will be accurate.
If the response in ohms or phase are not flat, you may be able to correct this via the cable compensation button next to the CAL button.
Hope this helps.🙂

Peter
 
Status
Not open for further replies.
Top Bottom