"I've never read anything indicating people worrying about that enough to measure the effect. "
And some people eat at McDonalds too.
Even at low levels, a speaker with high FMD sounds 'congested' compared to a speaker with low FMD.
I have problems listening to the JBL 4430 studio monitor (15 + horn) because it has quite a bit of FMD on certain program material. Same issue with the larger 4435 dual 15 monitor. The answer here proved to be a custom monitor with the 2204 woofer and 2342 HF horn, crossed at 100hz to dual subs.
And some people eat at McDonalds too.
Even at low levels, a speaker with high FMD sounds 'congested' compared to a speaker with low FMD.
I have problems listening to the JBL 4430 studio monitor (15 + horn) because it has quite a bit of FMD on certain program material. Same issue with the larger 4435 dual 15 monitor. The answer here proved to be a custom monitor with the 2204 woofer and 2342 HF horn, crossed at 100hz to dual subs.
That's an interesting insight. I assumed those differences were caused by thermal compression. If diffraction is involved - and I think you're onto something there - then wouldn't it be diffraction off of moving parts on the baffle (i.e. woofers) though?
In sighted listening, perhaps. But if one doesn't know how much "FMD" a speaker has... 😉
Full range drivers do indeed have doppler distortion. It is a recognised dissadvantage of using a single full range driver.
Textbooks of repute cover the issue. For any given cone area and acoustic level, the doppler distortion is easily calculated, with a formula you can derive with first year high school math.
It's even covered in my ancient copy of Acoustical Engineering, H F Olson, first published 1940. In the last edition (1960), it is on page 190, which has a usefull graph showing the doppler distortion for various power levels and cone diameter.
There are several reasons why you don't see coverage of doppler distortion in hi-fi/audiophile magazines, even though speaker engineers are well aware of it:-
1. Unlike other aspects of speaker perfomance eg flatness or otherwise of frequncy response, the amount of doppler distortion is set by two factors (cone area and power level) and there is nothing the speaker manufacturer can do about that. So there is no need to quote it in datasheets or measure it. You can just calculate it at any time.
2. Historically, doppler distortion was never a real concern. In the era of hi-fi getting widespread acceptance by consumers (ie 1950's), music was compressed to fit the limitted dynamic range of discs, so power levels were low. Speaker drivers were large, up to 15 inches, 12 inch common.
Practices in quoting the quality of quality audio are remarkably persistent. For instance, professional enginners have long known that total harmonic distortion is almost useless as a measure of amplifier (or speaker) badness, but it was the first way that reviews could do it, and they are still doing it.
However, these days, power levels are high and drivers are small. Doppler distortion is now important.
3. To measure doppler distortion, you need a low distortion microphone and low distortion and low noise microphone preamp. Such things were and are very expensive and beyond the resources of hi-fi/audiophile reviewers.
4. In audio reproduction up until the 1980's, the weakest link in the reproduction chain was the pickup. Indeed distortion, from tracing distortion and tracking error, is inherent in disc replay, even if you have a perfect cartridge.
5. In paper cone loudspeakers, cone breakup is another source of distortion which can easily be greater than the doppler distortion.
6. Doppler distortion is proportional to the power level. This means that at the important low level passages in music, doppler distortion is very low.
7. In sealed enclosures ("acoustic supension"), air distortion dominates. Compressing a fixed volume of air behind a cone is inherently non-linear. At modern power levels with today's small cone areas, air non-linearity in front of the cone is not entirely negligible.
Now we have CD's, and with the best of modern recordings, the weakest link in the chain is your speakers.
Last edited:
Presumably by "FMD" you mean "frequency modulation distortion" which is the alternative name for doppler distortion.
The fact is, FMD/Doppler with speakers of typical cone diameter range is always negligible at low program levels. If programme levels are low, the cone travel is low, so the cone velocity is low. If the cone velocity is low, FMD/doppler must be low.
If your speakers sound 'congested' at low levels, you have some other problem, perhaps the voice coil is touching the pole pieces, or the speakers have an unusually low impedance inducing some sort of cross-over distortion in the amplifier - that can happen with some unusual solid state amplifier topplogies, or your amplifier is marginally unstable with those particular loudspeakers connected.
Last edited:
"In sighted listening, perhaps. But if one doesn't know how much "FMD" a speaker has... "
Just because you can't hear, don't insult those of us that can hear.
When the vocalist sounds like she is gargling while singing, that's really bad FMD.
Just because you can't hear, don't insult those of us that can hear.
When the vocalist sounds like she is gargling while singing, that's really bad FMD.
Remember, I mentioned this on the AMT thread. 🙂
Yes, you'll get diffraction from several sources, BUT it depends on the wavelength (and practically speaking the intensity of that wavelength as it diffracts). Ex. Woofer's will have diffraction from the surround at higher freq.s.. but because of directivity often are suppressed in level relative to the average. Ex. tweeter reacting to a woofer's surround: not enough "sources" and not concentric, nor is the diffraction "angle" nearly as great as the loudspeaker baffle's edges. The loudspeaker baffle's edges most certainly have an effect but often at a lower freq. because it's further away from the tweeter and reacts to a lower wavelength, and sometimes it's suppressed in intensity because of the high-pass filter.
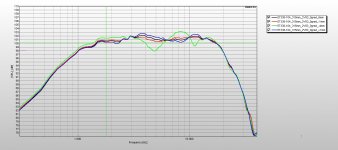
You can see several tweeters on this site that have been measured with various levels of "inset":
??-????????
What he hasn't shown is that it's very much a condition of intensity.. at lower intensity each diffraction "source" (if we think of it as discreet points of pressure), are very low and have decreasingly less effect as the tweeter's pressure is lowered. (..and likewise, it will have greater alteration as pressure for the tweeter is increased.)
Ex. the Morel ET338-104 (-4mm looks like cr@p)
Attachments
Last edited:
Why is compressing air in a sealed loudspeaker enclosure inherently non linear? In thermodynamics and fluid dynamics, air compressibility is linear and follows ideal gas law until very high compression ratios well beyond the several percent experienced by cone movement. PV=RT is about one of the safest bets in equations describing properties of air volume or density vs temperature.
Thanks for the link - I agree that the equation with compressibility factor and using gamma=1.4 for air is correct. It's nice to see the derivation by SL. Although I am not quite sure where the assertion that second order distortion is given by p_max-p_min/p_max+p_min.
The example shown is for a 12in driver experiencing 10mm of motion in a 40L box, which produces 1.75% second order, if the above relationship is true and justified as equal to second order HD. Not negligible, but I think at this level of motion, the driver inherent distortion is probably about 10% if not more.
In response to the OP's question from post 1: for a coaxial speaker with a CD mounted to a horn that is stationary, are we talking about distortion caused by the moving cone because it acts as the secondary expansion of the initial stationary horn?
For some coax's with a large horn that bypasses the speaker cone as a secondary expansion, would this effect not be an issue? Take for example, this coax from B&C:
http://www.parts-express.com/bc-15fhx76-15-professional-coaxial-speaker-60-x-40-8-ohm--294-5773
Last edited:
Let's assume the Ideal Gas Law (Kronig-Classius Equation) , PV = RT is true. R and T are constant. Thus P = k/V.
Let's assume the speaker cone movement is somehat extreme - this will make the basic concept clear by exageration.
Assume we have a square box, 300 mm x 300 mm x 300 mm. Assume one entire side is the speaker cone, vibrating in and out by 30 mm each way under tight control of the amplifier. When the cone moves in, the volume will be decreased by 30/300 ie decreased to 0.9000 of the rest value. Thus pressure goes up to 1/0.900 ie 1.1111 times the rest value. When teh cone moves out, the volume will be increased to 1.100 times the rest value. The the presure drops to 1/1.1000 ie 0.9.0909... of the rest value.
So the pressure cycle is non linear, because the ideal gas law is non-linear - it's a reciprocal relationship. In my example, the cone moving in 30 mm, the pressure goes up 1.1111 - 1.000 = 0.1111 and when the cone moves out it goes down 1.000 -0.90909 = 0.0909. So the pressure rise is different to the pressure drop - it's non-linear.
Not only is it, like all x times y relationships, NON-LINEAR, its not actually a precise law anyway. PV= RT is most certainly NOT one of the safest bets in science.
You got taught PV = RT in high school science. You get taught a lot of simplified stuff in high school. And if your science teacher was anything like most teachers, he never actually understood gas laws anyway.
In fact, when there is no heat added or taken from the air/gas, altering teh volume affects the temperature as well as the pressure, and the isentropic gas law applies:-
P. V^y = constant
where y is known as the adiabatic index, or ideal gas ratio of heats. y is approx 1.401 at room temperture, so you can see that P times V is nothing like constant.
I can derive y from first priciples if you like.
And air is not an ideal gas anyway. For engineering purposes, you can buy tables of correction factors for the isentropic gas law. - I have several versions.
Last edited:
I know about ratio of specific heats etc. and I know a lot more than high school science. Coming from most engineering principles where compressibility factors come into play are only at either Mach numbers approaching 1 or at high compression ratios, ideal gas law is in fact used for much of subsonic fluid mechanics such as Navier Stokes equations of fluid motion.
But seeing the SL derivation referenced by 454Casull provides a good basis, although I am not sure why 2nd order HD is given by P_max-P_min/P_max+P_min which the whole derivation hangs on. But SL is a smart guy and I will trust him.
I appreciate you bringing this up and explaining it, but lets skip the patronizing attitude:
Last edited:
You can't have it both ways. You stated that the ideal gas law is "one of the safest bets." That statement immediately shows you didn't know much at all. You can't claim you know it after I explained it.
You gave P.V = constant as a basis for believing that air in a box is linear. Since multiplicative relationships are by definition non-linear, that also shows you did not understand the topic.
I explained why speaker sealed boxes are non-linear even if the ratio of heats was unity - all you have to do is read it and follow my example.
See my simple example and work it thru yourself. You don't have to trust 454Casull, me, or anyone else. You only have to trust simple algrebra.
I included the bit about high schools and teachers, because experience tells me that many people mis-remember things they were taught at school, and commonly they were never taught properly anyway. The poor quality of science teaching in countries like Britain, USA, Australia etc is well documented and acknowledged by President Obama and others. And thinking that air in a box is a linear system is a common misconception.
Last edited:
Keit, relax man...
Yes P and V are inversely proportional, from PV=k... or P=k/V, I knew that. What I did not realize is that cone motion in vs cone motion out produces non-equal pressure differences, which are exaggerated for large cone motions. For small displacements, the inverse curve can be approximated with linear slope as often is the case. Large displacements, the curve matters, and I get that now.
Yes P and V are inversely proportional, from PV=k... or P=k/V, I knew that. What I did not realize is that cone motion in vs cone motion out produces non-equal pressure differences, which are exaggerated for large cone motions. For small displacements, the inverse curve can be approximated with linear slope as often is the case. Large displacements, the curve matters, and I get that now.
"You got taught PV = RT in high school science."
Nope. 😉
(..how properly it was taught is irrelevant, I wasn't taught it at all.)
..and you can "know a lot more than high school science" and still have never properly broached this subject, or even broached it at all.
-you are giving the US education system more credit than it deserves.. 😀
-also your response was a bit rude. 😱
when reviewing horn loaded systems such as Klipsch and big reflex, IIRC (?) Julian Hirsch would show an Acoustic Research sealed box to have less distortion than the horns (below cutoff)
hey - which of PWK's papers used the 15trx vs 15+T35? - I remember you mentioning greater distortion for the coax vs the offset tweeter,
I've heard flute gargle even with a 15cx in a Karlson - took a long sustained bass note - some may have been the cheap motor
hey - which of PWK's papers used the 15trx vs 15+T35? - I remember you mentioning greater distortion for the coax vs the offset tweeter,
I've heard flute gargle even with a 15cx in a Karlson - took a long sustained bass note - some may have been the cheap motor
Freddi,
Could this gargling simply be intermodulation distortion as a result of the mixing of the bass from the cone and highs from the CD/horn in the air space volume behind the K-aperture? That is, would it still be there without the K-aperture in place and the CD/horn had open face access to the outside?
Could this gargling simply be intermodulation distortion as a result of the mixing of the bass from the cone and highs from the CD/horn in the air space volume behind the K-aperture? That is, would it still be there without the K-aperture in place and the CD/horn had open face access to the outside?
Yep. That's pretty much it.
That's why bass reflex enclosures give lower distortion than sealed boxes - because the cone displacement is less in a bass reflex for the same bass acoustic power. But bass reflex has other issues.
1 mm would be a very tiny cone excursion by modern standardss, unles you are talking about full range electrostatics
To work out how much woofer movement you can tolerate, you first have to quantify how much total intermodulation distortion you can tolerate. How long is a piece of string? Researchers in the 1940's (eg Olson RCA) and 1960's (eg Philips) determined that 1% distortion is just on the threshold of the human ear to detect. I personally believe that with the low distortion music sources now available, and the widespread use of quality audio in the home, our ears have got a lot better. It seems clear that we can detect distortion much less than 1%, but how much less I don't know.
After you quantify how much distortion you can tolerate, you need to consider what sort of loudspeaker enclosure is to be used. Assuming for now that the driver itself is perfectly distortion free, there are a number of sources of distortion:-
Sealed box:-
Air nonlinearity behind the cone due to PV^y = constant;
Air non-linearity imediately in front of the cone.
Doppler distortion
Bass Reflex:-
All of the above, in smaller amounts, plus:-
Vent distortion due to PV^y = k
Vent distortion/noise due to edge turbulence.
Of all these, doppler is the easiest to calculate and is directly related to cone area and cone displacement.
The others are mostly reduced by reducing cone excursion, but not in a simple way. Obviously, behind-the-cone air distortion doesn't depend just on the cone excusrion, it depends on the box volume as well. The bigger the box, the lower the distortion. Even with a high displacement cone, the air distortion can be made as low as is desired, by making teh box big enough. The damping (carpet felt, rockwool, or whatever) also affects air distortion, and may increase or decrease it depending on how it is used.
And of course the driver itself will create distortion, both odd and even order.
So, perhaps you may care to clarify what you want to learn?
Last edited:
- Status
- Not open for further replies.