Interesting link.
Resonance Frequency
The author likes "DAP Alex plus" as a high loss adhesive between two layers of wood. (Constrained layer damping.)
David S.
Resonance Frequency
The author likes "DAP Alex plus" as a high loss adhesive between two layers of wood. (Constrained layer damping.)
David S.
Last edited:
Hi Simon,
I don't really know what to say to you. Plenty of people are very happy with their substantial plywood cabinets and I don't want to disuade any of them from something that they are satisfied with. I certainly see enough pro gear that uses heavy plywood for some of its positive properties, it is strong and tough and especially strong for a given weight. Drop an MDF cabinet on a corner and you will do some serious damage to it. Drop a good plywood cabinet on its corner and it lives to do another tour date.
But if we are talking more ideally, "what makes a better cabinet", then I would shy away from pushing cabinets in the stronger and heavier direction unless I could deal with the damping issue as well. Lots of people get excited with Finnish Birch or Baltic Birch, 107 ply, etc. etc. Too many diyers listen with their eyes and will swear that thicker and heavier must be better (which is why I am a lone voice on this subject). Not to sound like a broken record, but stiffer and stiffer isn't the best approach.
Note that the BBC preference was for thinner (12mm) plywood and heavy damping, rather than MDF or chipboard. I think they liked the inherent strength of it too.
David s.
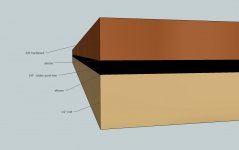
This boxes I glued from really thin Pergo, and molded inside by some composite thingy.
An externally hosted image should be here but it was not working when we last tested it.
Good listing but I'm not sure I want to know what "Sheep Absorption Coefficient" is.
David S.
OK, I have to admit that I didn't bother to read through all the posts in this thread, but wanted to throw my 2 cents in anyway, so please excuse my repeating anything that has been said here already...
The optimum material for baffles should have a combination of stiffness and damping/adsorption, maximizing the damping and minimizing the stiffness so that you are using the minimum amount of stiffness needed to withstand the internal pressure fluctuations. You can get a lot of damping by using alternating hard and soft layers, e.g. like 1/8" (3mm) thick hardboard (a pressed fiber board) alternating with 1/8" to 1/4" soft foam. Several alternating layers could be glued in a stack, say 1" thick total. The outer and inner layers should be the "hard" material, and should be joined together while the inner layers in each panel can float.
This would be mechanically functional, yet would suck up panel resonances like a champ.
-Charlie
The optimum material for baffles should have a combination of stiffness and damping/adsorption, maximizing the damping and minimizing the stiffness so that you are using the minimum amount of stiffness needed to withstand the internal pressure fluctuations. You can get a lot of damping by using alternating hard and soft layers, e.g. like 1/8" (3mm) thick hardboard (a pressed fiber board) alternating with 1/8" to 1/4" soft foam. Several alternating layers could be glued in a stack, say 1" thick total. The outer and inner layers should be the "hard" material, and should be joined together while the inner layers in each panel can float.
This would be mechanically functional, yet would suck up panel resonances like a champ.
-Charlie
May be I am wrong, but what's the purpose of inner layers if outer layers have joints that pass vibration from one to another?
something i've been working on. works very well if you miter all the joints and only glue the box together.
Attachments
Last edited:
Been in medical mode for several years so I'll have to dust off the engineering software and see what I still have lying around. Doubt I have the nastran solver still but I'm sure I have an algor version that should work well enough. When I get a little free time I'll see if I'm just way off my rocker or what!
Here's a thought experent that outlines the basic concept. Resonant frequency of a panel or beam is dependent on span, mass, and bending stiffness. Take a simple beam example. Bending stiffness is also a function of geometry. If a simple rectangular cross section it increases proportionately to the cube of thickness but of course there are other possible geometries (cylinder, tube, t or ibeam, and a bunch of non standard shapes).
Now it is entirely possible to construct two beams of equal length having identical resonant frequencies but vastly different masses, one being light and efficiently stiff and the other being massive and relatively less efficiently stiff.
Drive both beams with oscillator of equal amplitude at resonance. Does anyone doubt that the more massive and stiffer beam will have a lower amplitude deflection at resonance compared to the lighter and flimsier beam, even though their resonant frequency is the same?
This can be extended such that for any resonant frequency a more massive solution can be substituted for a less massive one. The only difference with simple panels is that when thickness increases the resonant frequency also increases as mass increases linearly and the efficiency of the geometry is constant (ie increases with cube). This should be provable in closed form but I'm too lazy at the moment. It would be more fun to investigate more fully with fea when I have the time.
Here's a thought experent that outlines the basic concept. Resonant frequency of a panel or beam is dependent on span, mass, and bending stiffness. Take a simple beam example. Bending stiffness is also a function of geometry. If a simple rectangular cross section it increases proportionately to the cube of thickness but of course there are other possible geometries (cylinder, tube, t or ibeam, and a bunch of non standard shapes).
Now it is entirely possible to construct two beams of equal length having identical resonant frequencies but vastly different masses, one being light and efficiently stiff and the other being massive and relatively less efficiently stiff.
Drive both beams with oscillator of equal amplitude at resonance. Does anyone doubt that the more massive and stiffer beam will have a lower amplitude deflection at resonance compared to the lighter and flimsier beam, even though their resonant frequency is the same?
This can be extended such that for any resonant frequency a more massive solution can be substituted for a less massive one. The only difference with simple panels is that when thickness increases the resonant frequency also increases as mass increases linearly and the efficiency of the geometry is constant (ie increases with cube). This should be provable in closed form but I'm too lazy at the moment. It would be more fun to investigate more fully with fea when I have the time.
I like the thought behind this. Too often here, one party quotes one book or another, whilst another counter-quotes from another author. Whilst we all get our information from SOMEWHERE, sometimes it can verge on more like a literary debate, rather than and actual experimental anaylsis.
This is the first time Ive heard anything that vaguely sounds like 'real' from-the-ground-up approach to investigating this. Any FEA would be interesting, to sate the quoters...
so...In 2 panels, both of equal rigidity, but differing masses, how would one measure the displacement/accn/vel/harmonic content, without adding mass and altering the outcome? or (maybe) also without adding damping?
the accelerometers I have used, have varied between small tri axial (maybe 20g), and larger single axis types (100-300g). The latter is certainly going to affect the resonance of a wooden panel of reasonable size, whether ply or pine.
Sorry but you are using a thought experiment to try and prove the point that is in dispute.
I'm not talking hypothetically but referring to two cases were researchers have done the test and published the figures. Harwood in his figure 14 (links are earlier in the thread) shows a cabinet built in a standard material thickness and again in double that thickness. The double thick cabinet has as many or more resonances and they are stronger. Specifically the 2nd 3rd and 4th major resonances are higher in magnitude. They are also higher in the frequency region where the ear is most sensitive so that the thicker cabinet will have more audible coloration.
The second example is figure 7.1 in Colloms' High Performance Loudspeakers. Barlow made a cabinet in 6, 12 and 18mm thickness. The primary cabinet resonances are at 60, 120 and 260 Hz approx. for the 3 thicknesses. The height of resonance is identical in each case.
Its more than a little frustrating when everyone says "a stiffer cabinet must have lower resonances" while ignoring valid examples that prove the contrary.
David S.
I've already said that I am going to more thoroughly digest the references you cite as well as investigate myself via FE when the time is available.
In the meantime I suppose you're just going to have to remain frustrated.
In the meantime I suppose you're just going to have to remain frustrated.
speaker dave, dude, if the enclosure material is the same OF COURSE the resonances are gonna occur in same frequencies, no matter how thick of a box u build. Thing is, with more solid enclosure the amplitude will be lower, meaning the resonances will be harder to detect, measure, hear. Do you agree with that? or should we start buliding enclosures out of shoe boxes? Is that what Collins advocates in that paper?
I'm not a Scientist or some kind of Psycho Professor ,but i would like for example that the case ( enclosure ) to be made from 0,2-0,4 mm Aluminium " plates " ,and when i say plates i mean plates joined by Nichel plated srews ,and some " cheap " plastic feet
Yes, Veikko, dude. Collins (Joan?) proves that shoeboxes are best. And she has lots of them.
Since, "OF COURSE the resonances are gonna occur in same frequencies, no matter how thick of a box u build" then we will all save money and use the old shoeboxes.
Glad we finally all agree.
David
p.s. Since I built my first speaker at the age of 7 by putting a car 6 x 9 in a square frozen turkey box and stuffing it with dirty clothes, I feel especially happy coming full circle back to shoe boxes. Has anybody compared Italian loafer boxes to construction boot boxes? Fast and lively vs. rugged and solid? Any opinions?
Since, "OF COURSE the resonances are gonna occur in same frequencies, no matter how thick of a box u build" then we will all save money and use the old shoeboxes.
Glad we finally all agree.
David
p.s. Since I built my first speaker at the age of 7 by putting a car 6 x 9 in a square frozen turkey box and stuffing it with dirty clothes, I feel especially happy coming full circle back to shoe boxes. Has anybody compared Italian loafer boxes to construction boot boxes? Fast and lively vs. rugged and solid? Any opinions?
Last edited:
Veikko, with low mass and low resonance the shoe box may be quite good in some respects. I fear, though, that sound will leak through the walls at quite high amplitude.
another salient poiint. at what point does acoustic opacity/translucency come into play as well as the sympathetic panel vibration? One reason i feel MDF isnt great at lesser thicknesses <12mm, is that it seems to MY ear at least like it is more transparent that other materials including BB ply. how mush truth there is to that in reality, or how to seperate panel vibration from sound just penetrating through the panel, I dont know.
now that I corrected the name (Colloms. Martin Colloms.) can we get back to 1 inch vs 3 inch MDF walls for enclosure, pls, spaeker dave?
Colloms (Martin Colloms's) paper seem to indicate there is no point. We could all do 1 inch MDF cabinets (or half inch for that matter.) and there is no benefit to develop a stiffer, more damped, less resonant cabinet. No matter that it goes against every serious speaker design philosophy?
I checked this post for spelling errors, speker dave, just to make sure there are no more needless distractions!
Colloms (Martin Colloms's) paper seem to indicate there is no point. We could all do 1 inch MDF cabinets (or half inch for that matter.) and there is no benefit to develop a stiffer, more damped, less resonant cabinet. No matter that it goes against every serious speaker design philosophy?
I checked this post for spelling errors, speker dave, just to make sure there are no more needless distractions!
- Status
- Not open for further replies.