Some would say bad luck.
We were selling KEF both before & after the decoupling grommets were introduced. After living with the grommets for a while, we started defeating them and everyone was happier.
The grommets concentrate all the reactive force in the driver chassis, reducing downward dynamic range.
dave
Power is the rate of work (use of energy)
ie if we do 100 joules of work it takes 100 joules of energy. If it takes 1 sec to do that work then we have 100 watts of power
In simple terms P = W/T ~ 1/(freq^2 x time).
dave
Cabinet output is proportional to acceleration which is the 2nd derivative of distance (integrate a constant twice and you get constant times x^2). Just as it should be if work done is proportional to 1/f^2.
dave
We could hear the improvement on music and even impulses ("boink" became "tick" with proper decoupling) and see a dramatic difference in waterfall measurements.
There were a few ill informed audiophiles who were never comfortable with the concept. To some, damping and decoupling might be alien. Most people got it though. (B&W copied it in the 801).
You, as a retailer, should have come to the factory and straightened us out. Laurie Fincham would have enjoyed that.
David S.
The Atlantic Ocean in the way... i have met Laurie Fincham at a CES, no chance to talk to him, i was just a kid then.
dave
I was thinking about the Harwood paper and was wondering whether some of the resonances are related (ie some higher frequency ones are harmonics of a lower one).
To that end i comped the graphs from the 1st comparison in the paper.
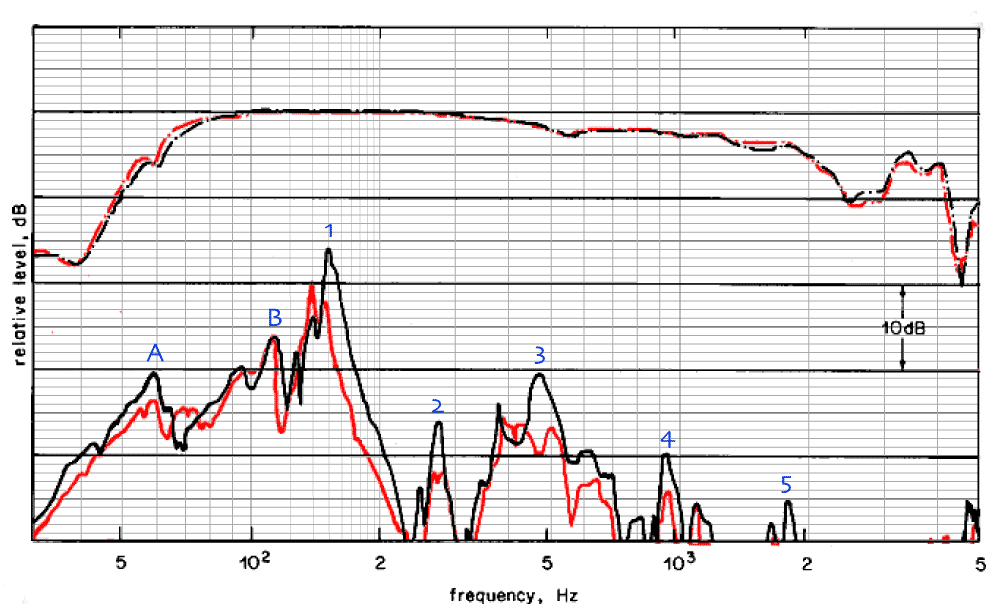
No question that the damping reduces the output of the some of the resonances, 10 dB for the one circa 500 Hz (#3).
If one looks at the big one at 140 Hz (#1), in a perfect situation would have harmonics would fall at 280, 420, 560, 1120, 2240, 4480 Hz. #2 falls in that list, #3 is more complex than a simple harmonic, but the next 2 are inside the envelope. #4/#5 are shifted down from the list. They do fall where you would expect harmonics of #3. I don't know enuff to be able to more than make an educated guess.
I do know that geometry has been known to shift things from an ideal harmonics train, a tapered TL for example shifts the harmonics.
Perhaps mondogenerater could throw an educated eye on this and comment.
dave
To that end i comped the graphs from the 1st comparison in the paper.
No question that the damping reduces the output of the some of the resonances, 10 dB for the one circa 500 Hz (#3).
If one looks at the big one at 140 Hz (#1), in a perfect situation would have harmonics would fall at 280, 420, 560, 1120, 2240, 4480 Hz. #2 falls in that list, #3 is more complex than a simple harmonic, but the next 2 are inside the envelope. #4/#5 are shifted down from the list. They do fall where you would expect harmonics of #3. I don't know enuff to be able to more than make an educated guess.
I do know that geometry has been known to shift things from an ideal harmonics train, a tapered TL for example shifts the harmonics.
Perhaps mondogenerater could throw an educated eye on this and comment.
dave
Attachments
Anyone have a link for the Harwood paper ... lots of reference to it, so would love to read it 😉
/Baldin
/Baldin
ok I take your word for that. None I have used have needed any EQ, using a charge amp at least. which is probably what you mean. well maybe. Im no expert, and there are many different size probes out there.
I Should say that I actually like your thinking on this subject, and the bracing philosophy, I may not totally agree on the whole damping/mass arguement, but essentially i agree. In ref to the Graph from the BBc paper, i think youre either correct, or perhaps it is partly at least the individual panel resonances, due to the edge battening compliance. with simlar panel weights and corner adhesion, Id expect a resonance for the side/s top/bottom, and maybe one each for the baffle and rear panel, IN A cuboid, rectangular prism trype box. If that is the case, it would seem that VERY stiff corners would reduce this, and a monocoque chassis i guess we'd expect there to be only one resonance, with artifacts. This would seem to advocate a monocoque 'box' IF the material chosen will resonate at a F that is easy to damp. OR controlled compliance corners....
Last edited:
Hahaha Its Imagination more than Education, I hate maths with a passion! But its a necessary evil.
I had missed that information, and now I understand even more your way of thinking.
Has anyone questioned that? I thought this part of the discussion was how to get past those box resonance frequencies, up or down?
I have noticed that I from time to time have a very hard time to follow the issues at hand, what is what etc, etc.
For example, this quote: "The notion that higher frequency resonances are narrower and therefore have miniscule probability of being excited is simply a canard."
Is it box frequency resonances that are referred to? And I've also seen mentioned both mechanical and air transfered box resonances mentioned, so I am apparently not always on par with the subject I guess. If it is me that you are referring to, it wasn't me that did the measurements, it was Linkwitz. His results was clearcut, lower resonances excites panels much more than higher resonances. This could be seen as well in the table where kinetic energy for various frequencies with the same driver was given. Much more energy was produced at lower frequencies compared to higher.
Maybe you talk apples and I oranges?
So with risk of being far too repetititive, here is some of what Linkwitz has to say on this subject:
"A cone type electro-dynamic driver is primarily a generator of mechanical vibration force and heat. It sets air into motion, but the reactive force of the air has insignificant influence on its behavior. For acoustic and mechanical reasons a driver is always mounted to a baffle of some form. Thus the forces generated in the driver try to set the baffle into motion. The resulting whole body movement is usually a small fraction of the cone movement and governed by the relative masses of cone and baffle. Mms vcone = Mbaffle vbaffle. Since the cone velocity vcone decreases with increasing frequency for constant SPL, the whole body motion is usually only noticeable at low frequencies and causes an insignificant reduction in SPL. This is a non-resonant phenomenon and no energy is stored.
Take, for example, two woofer drivers where each has a cone of 135 g moving mass and both are mounted in a box of 60 lb total weight or 27 kg mass. The box will want to move in reaction to the cone movement by 270g / 27000g = 1 /100 of the cone. Thus a cone displacement of 10 mm leads to a box displacement of 0.1 mm in the opposite direction. You can feel this readily by lightly touching the box. The effective movement is 9.9 mm, and a reduction in acoustic output by 0.1 dB which is insignificant.
Fundamentally different from this is the excitation of panel vibration modes. These are always resonant, store energy and can radiate sound. Usually the baffle or box surface is larger than the cone area. Thus small modal displacements can lead to more sound being radiated directly from the baffle or box at certain frequencies than from the cone. Knocking with your knuckle on a panel can give you a rough idea of the dominant mode frequency, though it might not necessarily get excited by the driver. This test can also tell you how stiff the panel is, when the pitch is high, or how well the panel is damped because it hurts to make it respond."
If I understand him correctly, he thinks air coupled box resonances trivial, that is, the box resonances excited by the air movement inside the box, and the mechanically coupled (driver frame attached to the baffle) excited box resonanses contributing the vast bulk of the box resonances.
Linkwitz take, of which I've cited a section of above, is actually the only section of text, figures and tables that I can manage to comprehend somewhat fully due to language barries and lack of knowledge in acoustics, physics etc, etc. So what is it that makes Harwood's results be so different, if they are?
And is it fair to compare Harwood to for example Linkwitz, that is a proponent of heavily braced boxes? Isn't that two totally different design philosophies?
I'll read the Harwood paper later, and also some other sources on the subject in due time, it is so much to try to absorb.
These are fair questions and deserve a fair answer.
As far as the part that you have quoted, I don’t think there is any conflict between Linkwitz and Harwood. Linkwitz is describing the simple physics of it, that accelerating the cone creates an equal reaction force to the cabinet and that since the cone is relatively light and the cabinet relatively massive then the cone will move more and the cabinet less. If the cabinet only had characteristics of mass, in other words there were no cabinet resonances to worry about, then there would be a miniscule broad band level loss from the cabinet motion and we would have no issues. As both Harwood and Linkwitz point out, the primary issue is that the cabinet masses, stiffness, geometry and damping turn it into a multi-resonant system where, at certain frequencies the cabinet is essentially transparent and the Q of the resonance will cause ringing that is likely to be audible.
What Harwood concentrates on, and the point I’ve tried to make in the thread, is that we typically ignore the beneficial role of proper cabinet damping. The typical audiophile assumption is that mass is good so “way mo’ mass is way mo’ betta” (or way more stiffness). Harwood’s point is simple, mass or stiffness changes may shift resonances up or down in frequency but substantial applied damping is required to guarantee a reduction in cabinet output at resonance. Reducing the height of the resonances is what you really want.
I don’t have the original paper but in Martin Collums' High Performance Loudspeakers book, he shows several plots that Barlow took. One is the cabinet panel output of 3 similar sized cabinets made of 6mm plywood, 12mm plywood and 18mm plywood. All three show a similar strong panel resonance with output almost as loud as the woofer. The frequency changes due to wall thickness (goes up in proportion to thickness) but it doesn’t drop in level at all. Harwood’s comment is that you need to have effective damping, meaning a pretty serious proportion of wall thickness and weight should be due to damping compound or damping layers. I don’t think he advocates thin cabinet walls so much as he makes the proper point that thicker walls will require even more damping material. For a given practical amount of damping you are better off with thinner walls because the damping to mass or damping to stiffness ratio is better. A simple design approach along Harwood's lines would be to first decide what thickness or weight cabinet you want, and then to make it with half the mass from plywood or MDF and the other half from damping layers.
My experience is that it is hard to shift resonances totally out of band. There may be exceptions such as a subwoofer with a low crossover, or planet 10’s 400 Hz crossover system. For the typical 2-way it would be very hard to get primary cabinet resonances above 2-3kHz. Harwood was designing monitors for the BBC and when he saw that raising resonances didn’t help, in that situation, he changed gears appropriately. Since the drive mechanism is more reaction force than internal acoustic pressure (Linkwitz makes that point, it was our experience at KEF, and it is the only explanation for the fact that most panel vibration plots show significant resonant activity at frequencies where internal stuffing would absorb the acoustical part of the radiated power) then raising resonances somewhat but leaving them in the woofer passband doesn’t fix anything.
As to Linkwitz and bracing, I don’t have the particular paper and your quoted section doesn’t make the case that this is a cure. I can’t imagine the Linkwitz would disagree with Harwood although he may show some advantages to bracing.
By the way. I highly recommend that people dig around the BBC website for any of the Shorter, Harwood, Mathers, or Stripp papers on Loudspeaker design. They had more knowledge on the subject than most of todays manufacturers.
BBC - R&D - Publications
Regards,
David S.
Thicker walls require MORE damping material? Really? so, say, 3 inch thick MDF cabinet wall would require more damping than 1 inch wall? You cant be serious!
as for 'For a given practical amount of damping you are better off with thinner walls..' I have a qusetion for you: Should I go with half inch thick walls? no, wait, thinner is better, right? 3mm walls then?
Once again confusing stiffness with damping. The issue is Q of resonance. As with all things mechanical or electrical, Q is the ratio of reactance to resistance. Viscous loss would be resistance, stiffness or mass would be reactance. Higher stiffness (or mass) will require higher damping to maintain the same Q. Higher stiffness (or mass) with the same amount of damping will increase Q and raise the height of the resonance.
I don't make this stuff up, guys.
Thicker walls may decrease width of the resonance ('higher Q') in the way you describe, bit it certainly doesn't increase the height (amplitude) of the resonance as you stated.
It may be a narrower bandwidth resonance but of significantly lower amplitude, thus damping is less critical. Which is common sense really, even if at odds with your claim.
It may be a narrower bandwidth resonance but of significantly lower amplitude, thus damping is less critical. Which is common sense really, even if at odds with your claim.
And I'll add that I need to look at the original publications you cited, as in all of my experience with both FEA and measured performance of panel resonances (in a different application, military R&D in that case), when both stiffness and mass are increased in a panel the energy required to produce a resonance of a given height increases proportionately. Resonant frequency may be maintained but amplitude of resonance is not. The situation you describe sounds more like increasing stiffness with mass held constant. In the case you may drive up resonant frequency but do relatively less good wrt amplitude.
Speaker Dave, thank you for your recent posts which I found very informative. They still don't, to my mind, explain why thick plywood baffles sound so darned good and natural. Can you relate the theory you understand so well to the real-world scenario of plywood sounding so natural?
I realise I risk sounding ignorant with this question but it's a risk I'm willing to take for enlightenment!
(The lines of thought I've had are that in my case - large 24mm BB ply baffles - the resonant frequency is low enough to be well away from the ear's sensitive upper-mid range.)
Thanks,
Simon
I realise I risk sounding ignorant with this question but it's a risk I'm willing to take for enlightenment!
(The lines of thought I've had are that in my case - large 24mm BB ply baffles - the resonant frequency is low enough to be well away from the ear's sensitive upper-mid range.)
Thanks,
Simon
Last edited:
Q and resonance height will go hand in hand. In fact resonance height will be proportional to 20 log Q, as it is with most mechanical resonances. If we change panel thickness alone I wouldn't expect to see any Q or resonance height change.
This is what the Barlow measurements showed. If you have measurements or simulations to the contrary, I'd like to see them.
Wall thickness is interesting. As you know the stiffness goes up approx. to the cube of thickness of an issotropic material. Mass goes up in proportion. Panel resonance goes up as the square root of the ratio stiffness over mass, so in the end resonance is proportional to thickness. If we want to push up resonance by a decade we would need 10 times the material thickness.
Generally our materials have little inherent damping (MDF, particle board, plywood) so we must apply a seperate layer of damping. As we increase thickness or mass the damping required for the same Q must also go up. It seems like mechanical impedance will quadruple for a doubling of wall thickness, so if anything, Q would go up for thicker walls?
David S.
An elaboration on your results would be appreciated (ie examples etc). Particularily the "more energy required
bit.
dave
- Status
- Not open for further replies.