Tests show that with LF standing waves in a room, once excitation near but not on a resonance is turned off, the tone shifts to the nearby peak and continues.
Just like the tuning fork isn't that just the resonance taking energy from the portion of the excitations bandwidth?
dave
To achieve very good downward dynamic range (DDR) you need better then 20-30 dB.....
Somewhere between these curves * some konstant, is the likelihood of exciting a resonance when the stimulus is music.
If a resonance is not excited it is as if it does not exist.
Relative to the recent discussion of granite, it also shows why, thou it may ring like a bell when externally stimulated with a broad band signal, with music as the stimulus, they could be made quite non-resonant.
dave
Firstly, Mathematically, ONE can ASSUME music to be a broadband noise. Testing with weighted noise, pink, brown or noise BW weighted toward P10's(or others') excitation probability, would be interesting, although a resonance is ALWAYS excited. The more important question would be WHAT level of resonance is acceptable.
Some quote -25 to -30 dB, which is fine. stiffness alone cannot cure the problem, at some point Newtonian physics has its own influence. unless someone has invented some 'skyhooks'.....like the irresistable force vs the immovable object...... cone + airload mass vs panel mass + compliance, momentum etc. a PERFECT box weighing 10 times the cone mass (i know daft example) will still be displaced by a 10th that of the cone, as long as V is equal. precisely why weight is important to damp LF cabinet vibrations as much as possible. Precisely why those 'naked' OB set ups bug me so much.....hang a driver from a cord and hope for bass....
And as for Granite...it will ring. as will ceramic. And my God, so will steel!!! But with the correct damping substrate, this can be minimised. In my limited experience, despite its downfalls, I have found MDF much easier to damp than BB ply. a layer of silicone sealer to glue on some cheap felt I had, MORE than did the job. and BTW the felt was only 2mm thick... and polyester....maybe plasterboard lath would mate with the granite nicely....hmmmmmm
Last edited:
Let's refine that definition... plywood with lots of plys and no voids (or well filled voids, is the best easily available material for building cabinets using standard wood-working tools.
dave
There are lots of claims of void free plywoods, can someone please direct me to a standard for such a product. Here in Sweden, I've seen a few standards used by different manufacturers, and they all relate ONLY to the surfaces, so I would like to get hold a void free standard to see what it is about.
Well, for the number of ply, a "standard" grade you can often find is 13 ply for 3/4".
You can often find some extremes, like this Aircraft Birch Plywood... 20 ply for 10 mm...
The most extreme I've seen so far is a 2mm, 3-ply that is bendable 180 degrees. Finnish origin.
Another way would be a sandwich construction. It could be made very stiff and very light.
/Baldin
I've seen it suggested that for a sandwich construction, an aluminum honey comb sheet placed between two sheets of something suitable would produce a very stiff and quite light box. Haven't seen it done though.
We want mass and damping rather than light weight strength. Multiple layers with a high proportion of damping material (preferably internal) is the better way to go.
David S.
This way, you will not be able to get rid of low frequency wall excitations, they contain too much energy. I think this is what Planet10 has been trying to convey (or has explained) all along. I don't think it has sunk in everywhere (if this is actually what he means)?????? As you make the box stiffer and stiffer, you will rise the frequency where the box will resonate?, and the higher the frequency, the less energy they contain, and thereby, they will have a much harder job excite the box walls. (Maybe I've got it all wrong??????? Please, don't force me to go hiding, I've so much to learn here)
Take a look at the Harwood paper. Based on his listening tests there was a constant threshold of audibility for resonances that occured above 500 Hz. Resonances below that could be stronger for equal audibility. Also, the energy level of resonances he measured on a viriety of cabinets was fairly flat from 100Hz to 2000Hz (with some scaling due to cabinet size). Probability of excitation isn't falling as your graph suggests. Both his graphs and his comments show that raising cabinet resonances by making walls stiffer can make resonances more audible.
David S.
With no experience of my own, and limited theoretical knowledge, I have a very hard time to believe the above to be correct. I'm not that very fond of listening tests either. However, I'm often wrong, and the energy load of resonances between 100 to 2000 Hz being almost equal, must be easy to verify for one who knows where to look. I guess I have to re-read the paper before making further assumptions. I'm very tempted to make some test boxes myself before I start my own project, but then I won't finish before I die.
speaker dave, I'm trying to learn here, I might have missed it, so can you please give a brief explanation as to why the way you prefer is the better one? I'd like the physics behind the idea, so that I can compare it with how I understand Planet10's way of thinking.
All absorption coeffecients I have seen tell me that foam is pretty much useless. While Fibreglass being one of the better absorption materials (depending on its density).
I don't mean coefficients, I mean practical results. Memory foam glued to internal surfaces of concrete damp resonances caused by reflections better than other materials, be they in the whole volume, in the middle, or on internal walls. If to speak of structural resonances, concrete with uneven gravel and with uneven thickness of walls does not need to damp them. But when I need to damp resonances of surfaces I prefer good old linoleum to all patented materials.
I've seen it suggested that for a sandwich construction, an aluminum honey comb sheet placed between two sheets of something suitable would produce a very stiff and quite light box. Haven't seen it done though.
I used perforated aluminiun sheets in sandwich for a lid of my concrete horn subwoofer under the floor. Works great.
Last edited:
As you make the box stiffer and stiffer, you will rise the frequency where the box will resonate?, and the higher the frequency, the less energy they contain, and thereby, they will have a much harder job excite the box walls.
With no experience of my own, and limited theoretical knowledge, I have a very hard time to believe the above to be correct. I'm not that very fond of listening tests either. However, I'm often wrong, and the energy load of resonances between 100 to 2000 Hz being almost equal, must be easy to verify for one who knows where to look. I guess I have to re-read the paper before making further assumptions. I'm very tempted to make some test boxes myself before I start my own project, but then I won't finish before I die.
speaker dave, I'm trying to learn here, I might have missed it, so can you please give a brief explanation as to why the way you prefer is the better one? I'd like the physics behind the idea, so that I can compare it with how I understand Planet10's way of thinking.
I can't copy from the PDF as it is protected but look at figure 5 for example and you will see the breakthrough from the sides and back of a cabinet realative to the woofer output. The big resonances are in the 100 to 300 range but there is strong cabinet output up to 2kHz. I don't think there is a theoretical basis for saying "the higher the frequency, the less energy they contain" or the harder it is to excite them. Note that the level of resonances is based on a standard constant voltage sweep, but the detection thresholds are based on his listening tests with speech and music. Any falloff in music spectrum is already factored in.
As to the physics of the idea, cabinets, like any mechanical structure have basic properties of mass, stiffness and damping. Audiophiles tend to get excited about stiffness or mass but usually overlook the damping aspect. From this we get very solid cabinets made of granite or ultra thick wood, but all that is achieved is that the resonances are pushed up the better part of an octave (at great expense). The BBC Harwood paper takes a fresh look at what an ideal cabinet is.
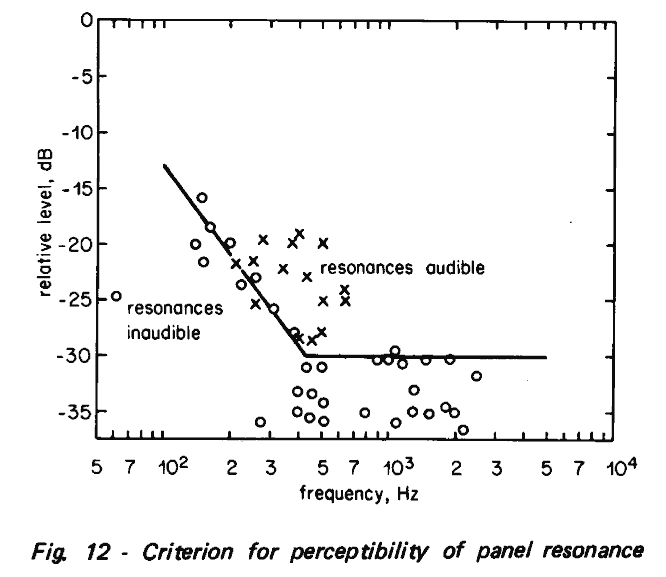
His figure 12 shows the primary resonances he detected when examining a number of cabinets and which ones were audible vs. which ones weren't. Most of the troublesome ones were in the 300 to 700 Hz range above a level of 30 dB below the woofers output level. (fig 12) Above that frequency the -30 threshold still held, below about 400 Hz the resonance level could rise without detection.
Moving the frequency of resonance up isn't going to help. You need to reduce its level. This means adding damping in some form. He liked adhering roofing tar paper to the inside surface of the cabinets. I've had better luck with internal layers of damping material. (Constrained layer damping. We studied this a lot at Snell.)
The point that Harwood makes is that damping needs to be in proportion to the mechanical impedances of the cabinet walls. That is, if you add mass (higher mechanical impedance) you will need more damping to get the same Q. The same if you increase stiffness. His figures 13 and 14 shows a monitor cabinet where they used a standard wall thickness and a double wall thickness. Damping the standard thickness got resonances below his threshold. The cabinet with double wall thickness, even with damping, was always above the threshold of audibility.
So, heavy and stiff is not a substitute for well damped and can make it more difficult to reduce cabinet resonant output.
This is a great example of how audiophile notions can be totally at odds with good engineering.
David
I can't copy from the PDF as it is protected but look at figure 5 for example and you will see the breakthrough from the sides and back of a cabinet realative to the woofer output. The big resonances are in the 100 to 300 range but there is strong cabinet output up to 2kHz. I don't think there is a theoretical basis for saying "the higher the frequency, the less energy they contain" or the harder it is to excite them. Note that the level of resonances is based on a standard constant voltage sweep, but the detection thresholds are based on his listening tests with speech and music. Any falloff in music spectrum is already factored in.
As to the physics of the idea, cabinets, like any mechanical structure have basic properties of mass, stiffness and damping. Audiophiles tend to get excited about stiffness or mass but usually overlook the damping aspect. From this we get very solid cabinets made of granite or ultra thick wood, but all that is achieved is that the resonances are pushed up the better part of an octave (at great expense). The BBC Harwood paper takes a fresh look at what an ideal cabinet is.
His figure 12 shows the primary resonances he detected when examining a number of cabinets and which ones were audible vs. which ones weren't. Most of the troublesome ones were in the 300 to 700 Hz range above a level of 30 dB below the woofers output level. (fig 12) Above that frequency the -30 threshold still held, below about 400 Hz the resonance level could rise without detection.
Moving the frequency of resonance up isn't going to help. You need to reduce its level. This means adding damping in some form. He liked adhering roofing tar paper to the inside surface of the cabinets. I've had better luck with internal layers of damping material. (Constrained layer damping. We studied this a lot at Snell.)
The point that Harwood makes is that damping needs to be in proportion to the mechanical impedances of the cabinet walls. That is, if you add mass (higher mechanical impedance) you will need more damping to get the same Q. The same if you increase stiffness. His figures 13 and 14 shows a monitor cabinet where they used a standard wall thickness and a double wall thickness. Damping the standard thickness got resonances below his threshold. The cabinet with double wall thickness, even with damping, was always above the threshold of audibility.
So, heavy and stiff is not a substitute for well damped and can make it more difficult to reduce cabinet resonant output.
This is a great example of how audiophile notions can be totally at odds with good engineering.
David
David, was the midrange baffle on the old Snell Type A (the speaker I miss the most) made of cardboard and a lot of kind of soft putty around the tube that held the 5"?
I visited the company just after Peter's death with the late distributor Peter Qvortrup and saw the whole process of making the A.
Peter
David, was the midrange baffle on the old Snell Type A (the speaker I miss the most) made of cardboard and a lot of kind of soft putty around the tube that held the 5"?
I visited the company just after Peter's death with the late distributor Peter Qvortrup and saw the whole process of making the A.
Peter
I think it was masonite rather than cardboard. That allowed Peter to score it and bend it to the large convex surface that was so good for low diffraction. Yeah, lots of putty and felt and other bits to smooth the response. A little bit amateur but very effective in the end.
Ahead of its time.
David S.
although a resonance is ALWAYS excited
Why? Sufficient energy must be pumped in (within the resonances bandwidth) to overcome the "inertia" provided by the inherent damping of the box material.
dave
This way, you will not be able to get rid of low frequency wall excitations, they contain too much energy. I think this is what Planet10 has been trying to convey (or has explained) all along. I don't think it has sunk in everywhere (if this is actually what he means)?????? As you make the box stiffer and stiffer, you will rise the frequency where the box will resonate?, and the higher the frequency, the less energy they contain, and thereby, they will have a much harder job excite the box walls. (Maybe I've got it all wrong??????? Please, don't force me to go hiding, I've so much to learn here)
You are one of those getting it.
dave
I can't copy from the PDF as it is protected but look at figure 5 for example and you will see the breakthrough from the sides and back of a cabinet realative to the woofer output. The big resonances are in the 100 to 300 range but there is strong cabinet output up to 2kHz. I don't think there is a theoretical basis for saying "the higher the frequency, the less energy they contain" or the harder it is to excite them.
I can, but don't have time. I reread the Harwood doc. Nothing in it says anything that counters my argument. A couple points.
1/ at least a couple times they state this should be considered preliminary and more work needs doing. This is particularily evident in the criterion graph. Above 700 Hz there are no Xs (resonance audiable). You could draw the curve anywhere for f>700 as long as it was above the Os.
2/ the assumption is made that lower Q box resonances are better than high Q ones. Toole presents real data that refutes that assumption, making a significant part of Harwood's paper moot.
3/ i would be loath to build any box with an unsupported 12" wide panel.
It does have a couple things that add to support to my techniques. One is the suggestion of a primitive version of my holey driver brace. Another was some comments about the "invisibility" of the box at resonance. If these resonances occur at high enuff frequencies that the internal air space damping is effective, then signal will have been attenuated before it passes thru the box walls.
The paper adds some interesting data points and some things to think about, but it hardly tells you everything you need to know. Just another set of information to add to all the other undefinitive research done.
dave
Attachments
I don't think there is a theoretical basis for saying "the higher the frequency, the less energy they contain" or the harder it is to excite them.
I'll work on digging out the text book equation that relates frequency to energy which gives the inverse square criterion.
dave
2/ the assumption is made that lower Q box resonances are better than high Q ones. Toole presents real data that refutes that assumption, making a significant part of Harwood's paper moot.
dave
He doesn't actually talk about box Q but the rather the level the peak of breakthrough energy. Peaks higher than -30dB re. the woofer level where, in his tests, inaudible. I'll agree that above 1000Hz he doesn't have enough data points to be too definitive about the threshold.
Toole quotes Freyer and others that show that, all other things being equal (peak level) then higher Q is less audible than lower Q. In fact for a doubling of Q then the resonance peak needs to be 3dB higher. What he overlooks (as well as every one that quotes him) is that with natural systems if you reduce damping to double Q then the peak level at resonance will go up by 6dB. In other words, in practice, higher Q is more audible than lower Q.
Would you really believe that damping resonances makes them more audible rather than less?
David S.
all other things being equal
Does that assumption hold in the real world?
Would you really believe that damping resonances makes them more audible rather than less?
Adding damping would certainly remove the validity of your assumption above, so maybe.
In a previous life my common sense would agree with you. But adding damping adds mass without stiffness. If that makes the difference of exciting or not exciting a resonance then clearly no damping/no resonance would be less audiable than add damping/get a resonance.
My goal is to make a box where resonance is moot because the resonance is never excited.
dave
The Freyer tests used an electrical setup where a flat straight through path has a side chain of variable Q. As Q is varied they adjust the height of the peak and then test for audibility. That is what I meant by all other things being equal: that the peak height was artificially held constant. With mechanical systems Q and peak height are intertwined.Does that assumption hold in the real world?
eh?Adding damping would certainly remove the validity of your assumption, so maybe.
My goal is to make a box where it is moot because the resonance is never excited.
This is where we started. How do you have a resonance that is never excited?
David S.
Concrete Canvas could make for easy rock solid speakers.. just blanket a frame and add water, voila!
Last edited:
D
My goal is to make a box where resonance is moot because the resonance is never excited.
It is impossible. All you can do, is to get as low Q as possible, and resonant frequencies as far as possible from spectra you reproduce.
I saw that nice pictures about making of speaker boxes from stone. Quite expensive game, and quite useless, because of the effort to make something useful from uniform material, especially making flat, even and shiny surfaces.
Here is another example: rough, but good. Non-uniform material, uneven thickness of walls, no resonant surfaces. The trickiest thing was front panel, I made it as a sandwich that includes perforated aluminium as well.
Attachments
It is impossible. All you can do, is to get as low Q as possible, and resonant frequencies as far as possible from spectra you reproduce.
It is not possible to make a box that doesn't have resonances. You can move them such that it is unlikely they get excited.
And despite what dave s says, Toole (& co) have sat people down in blind tests and discovered that low Q resonances are more audiable than hi Q resoances.
Before i ran across any of that research, i had already decided that hi Q resonances were preferable for my box approach as they have less area under the curve, and a smaller bandwidth that will accept energy that would excire the resonance.
dave
This is where we started. How do you have a resonance that is never excited?
Put it where there is insufficient energy to excite it... pretty simple.
Feed it with a sufficiently large sin wave signal tuned to its bandwidth and it will ring like crazy. Feed it with music (transient by nature) and you are unlikely to get sufficient energy to excite it.
dave
eh?Adding damping would certainly remove the validity of your assumption, so maybe.
Just like the oft seen question, what would happen if all things equal, we changed just the....
Things are so inter-related it just isn't a realistic question.
Add damping, you are adding mass without adding stiffness, things are no longer equal.
dave
Results of low Q resonances can be corrected electronically. But there is no way to correct high Q resonances, except to absorb energy from them, i.e. lowering their Q. Lowering Q can be achieve by 2 ways: either to turn an energy into heat inside of the box and it's walls, or by radiating it outside. However, if that guys who sat people down lowered Q by allowing more of energy of oscillations to go away radiated into the room, it is understandable. I mean another way to lower down Q: to make uneven internal surfaces of the box, to use uneven density of the material, and turning an energy into heat by using of damping means inside of the box.
It will be excited by any amount of an energy. And since it is non-linear, the higher is an energy, the more of by-products of the 2'nd and higher orders are generated.
Edit: here is an experiment for you. Take a guitar and sing near it. It answers, because it has high Q resonators. Now remove that resonators (strings) and try again. Do you hear the difference?
Put it where there is insufficient energy to excite it... pretty simple.
It will be excited by any amount of an energy. And since it is non-linear, the higher is an energy, the more of by-products of the 2'nd and higher orders are generated.
Edit: here is an experiment for you. Take a guitar and sing near it. It answers, because it has high Q resonators. Now remove that resonators (strings) and try again. Do you hear the difference?
Last edited:
- Status
- Not open for further replies.
- Home
- Loudspeakers
- Multi-Way
- What are the characteristics of a better material for enclosure?