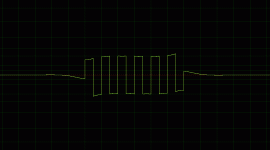
That's right to some extent. Let's say it fixes it to the best theoretically achievable amount for a given corner frequency and amplitude response 😉
Those slopes as seen in your example completely disappear with a linear-phase high-pass once you are high enough in frequency (3x the corner frequency is already high enough for the "dips" to become invisible for my LR4-highpass, see attachment).
Anyway I'm not convinced that this -- the optically "perfect" square, regarding the flat tops -- really relates to anything acoustically relevant. IHMO the phase relationships at different frequencies do matter much more. Note the visible lagging of the fundamental in my earlier graph, for the minimum-phase version.
- Klaus
Attachments
Last edited:
Ah, you're right Klaus, thanks! I just tried it and zeroing the phase of the woofer's 20 Hz highpass does flatten the tops considerably.
Last edited:
If the phase is linear and amplitude flat from the fundamental and up, flat tops result. The flat tops are an indication of that. But there is a caveat. Any time a system is corrected to linear phase the impulse response of the system will peering to some degree. Also, if you only correct crossover make the system linear phase through the crossover then the impulses of the HP and LP crossover sections will also peering, which may be observed off axis. Thus it's more so for the HP section. Thus, if possible it is best to use a TWP crossover (i.e. B, etc). But those have other issues. Still, I am a fan of being able to apply phase correction to linear the system phase and have prototype software to do just that which I have been helping develop.
Hi John
Sorry but "peering"? Not familiar with that term.
And let me ask this - why the interest in square wave reproduction? I mean it might look good, but there is no data that suggests that a system that reproduces square waves will sound any better than one that doesn't. The ear above a certain point is not phase sensitive so there is every reason to believe that the quest for the "holy grail square wave" is just that, a journey without a point.
I think John meant prering -- ringing before the impulse.
Audibility aside, the engineer in me finds it offensive to have the waveform coming out of the speaker look nothing like the waveform that went in. As someone else said, we'd be outraged if an amp did that to the signal. 😉 So, it all gets down to tradeoffs. If you can preserve the waveform without sacrificing something more important, why not do it? That's what everybody is looking for -- not preserving the waveform to the exclusion of all else but trying to minimize the compromises you need to make to do it.
The data is sparse but there is evidence to suggest it's more audible with headphones than with speakers in rooms and more audible with test signals than with dense music. So the effect is easily masked but it's not nonexistent.
Audibility aside, the engineer in me finds it offensive to have the waveform coming out of the speaker look nothing like the waveform that went in. As someone else said, we'd be outraged if an amp did that to the signal. 😉 So, it all gets down to tradeoffs. If you can preserve the waveform without sacrificing something more important, why not do it? That's what everybody is looking for -- not preserving the waveform to the exclusion of all else but trying to minimize the compromises you need to make to do it.
Personally, for me the thing is settled. I have 100% scores in true ABX testing with any music containing some LF attack transients like bassdrums, when trying to tell linear phase from miminum phase (looking at the region below 1kHz or so), with both pairs of my speakers (which both are BR designs, one of them with 6th order alignment at 50Hz where the influence of the massive GD is pretty obvoius). It's more a thing of a "body-feeling", the more you try to force concious listening during the test the less you may note the difference in perception (typical also for many other audio related ABX-tests), also high SPL tend to lessen the preception threshold for me. Howerver, once one is accustomed to the difference you immediately note that dispersion effect anywhere you listen, especially again with bookshelf speakers with high tuning or with badly integrated subwoofers (say with a non optimized LR4 crossover at 80Hz, plus a subsonic, then the bass is really late).
And also, with linear phase bass/mid I could for the first time discriminate absolute polarity, albeit I got only consistent 100% ABX results with a testsignal (sort of an electric bass drum) which is a pretty assymetric and a short transient. This seems to be due to the fact that the neurons in the ear fire only during the positive relative pressure part of a waveform (there is a section in a paper by David Griesinger on this). Before phase linearization the phase shifts blur the differences in the resulting waveform at the eardrum so it is not easy to tell a difference, let alone tell which one has the stronger impact. With linear phase it's easy, the one with the higher/broader peaks in the positive half is the "fatter" one.
For higher frequencies (> 1kHz) I could not find a significance of any moderate phase distortion. All this with a single loudpeaker, of course. Once we listen to stereo things change, then the L to R matching in phase/GD becomes the limiting factor, degrading imaging (depth, especially). We talk about L/R-drifts in the region of 10uS there. People who have studied this in more detail (such as developers of truly working room correction systems like Dr.Ulrich Brueggemann) have found the L/R-matching of the step response within the first 10mS or so is needed for a stable localization. When this is achieved one can start to detect image degradation from Jitter of the DAC etc...
These are all findings of a group of people which took part in group delay listening tests we conducted in a german forum (true blind tests, only the members who manipulated the files knew what was done). It was foound that L/R-matching is at least one order of magnitude more important than the phase characterstic on itself, given the phase is considerably smooth (but not necessarily flat).
- Klaus
And also, with linear phase bass/mid I could for the first time discriminate absolute polarity, albeit I got only consistent 100% ABX results with a testsignal (sort of an electric bass drum) which is a pretty assymetric and a short transient. This seems to be due to the fact that the neurons in the ear fire only during the positive relative pressure part of a waveform (there is a section in a paper by David Griesinger on this). Before phase linearization the phase shifts blur the differences in the resulting waveform at the eardrum so it is not easy to tell a difference, let alone tell which one has the stronger impact. With linear phase it's easy, the one with the higher/broader peaks in the positive half is the "fatter" one.
For higher frequencies (> 1kHz) I could not find a significance of any moderate phase distortion. All this with a single loudpeaker, of course. Once we listen to stereo things change, then the L to R matching in phase/GD becomes the limiting factor, degrading imaging (depth, especially). We talk about L/R-drifts in the region of 10uS there. People who have studied this in more detail (such as developers of truly working room correction systems like Dr.Ulrich Brueggemann) have found the L/R-matching of the step response within the first 10mS or so is needed for a stable localization. When this is achieved one can start to detect image degradation from Jitter of the DAC etc...
These are all findings of a group of people which took part in group delay listening tests we conducted in a german forum (true blind tests, only the members who manipulated the files knew what was done). It was foound that L/R-matching is at least one order of magnitude more important than the phase characterstic on itself, given the phase is considerably smooth (but not necessarily flat).
- Klaus
I said, but I should have been more specific, that I was talking about phase "above a certain point", namely 500-1000 Hz. Below that there is evidence of phase detection, but not above that. GD, yes, but not absolute phase. I would like to see some published data on the tests that were performed.
The point about "the waveform coming out of the speaker look nothing like the waveform that went in" is incorrect IMO, to wit THD. Everyone obseses about it for this exact reason, and yet it is virtually irrelavent. "If you can preserve the waveform without sacrificing something more important, why not do it? " This is also incorrect IMO because everything in loudspeaker design is a tradeoff and if you try and correct something that is unimportant then you have to be compromising somerthing that is. "the engineer in me" finds it a poor design philosophy to design arround things that don't matter.
The point about "the waveform coming out of the speaker look nothing like the waveform that went in" is incorrect IMO, to wit THD. Everyone obseses about it for this exact reason, and yet it is virtually irrelavent. "If you can preserve the waveform without sacrificing something more important, why not do it? " This is also incorrect IMO because everything in loudspeaker design is a tradeoff and if you try and correct something that is unimportant then you have to be compromising somerthing that is. "the engineer in me" finds it a poor design philosophy to design arround things that don't matter.
Last edited:
Mr. Geddes, do you have any recommended papers on physcho-acoustics dealing with phase sensitivity that could be shared? I know very little about this subject and since it deals directly with what this post is investigating it would be valuable information.
I did find this article after a quick look at wiki-pedia.
http://forums.klipsch.com/forums/storage/3/1027021/7805blauert.pdf
It's from May of 1978, but they state along with several sources that phase coherence is important in the "critical bands". I would assume that "critical bands" is in the area of speech, say 300Hz-3000kHz. If any newer or more relevant information can be found, please share.
Also, the paper states that group delay is equal to the derivative of phase shift.
Td = d[b(w)]/dw.
So what does this mean physically?
I see this relationship as follows: If our system is incoherent (not phase aligned) then we get a shift in group-delay. If we have no phase shift (b(w) = 0) then we are coherent (phase aligned) then we have no group delay. If this is correct then our phase alignment plays directly into group-delay, which is an important factor in high fidelity systems. Correct?
This is all my sort of 'first pass' understanding of this subject, it may very well be wrong but I'm interested in this material and would like to see this subject discussed more. So everybody get back to posting!! 😀
I did find this article after a quick look at wiki-pedia.
http://forums.klipsch.com/forums/storage/3/1027021/7805blauert.pdf
It's from May of 1978, but they state along with several sources that phase coherence is important in the "critical bands". I would assume that "critical bands" is in the area of speech, say 300Hz-3000kHz. If any newer or more relevant information can be found, please share.
Also, the paper states that group delay is equal to the derivative of phase shift.
Td = d[b(w)]/dw.
So what does this mean physically?
I see this relationship as follows: If our system is incoherent (not phase aligned) then we get a shift in group-delay. If we have no phase shift (b(w) = 0) then we are coherent (phase aligned) then we have no group delay. If this is correct then our phase alignment plays directly into group-delay, which is an important factor in high fidelity systems. Correct?
This is all my sort of 'first pass' understanding of this subject, it may very well be wrong but I'm interested in this material and would like to see this subject discussed more. So everybody get back to posting!! 😀
Blauert is certainly a place to start, but its an excedingly complex topic. For example, both Blauert and Moore claim that group delay is not a significant issue in "typical" setups, but both do admit that it can be audible. Neither recognized that group delay audibility is very dependent on absolute SPL, getting much more audible at higher SPL than lower. One cannot therefor simply conclude that group delay is not audible in a more extreme setup or at higher sound playback levels. I happen to believe that it is a key reason why some systems sound so much better at higher SPLs that others particularly when one is forced to elliminate nonlinear distortion as audibly significant.
That said, if group delay is only marginally audible then absolute phase certainly cannot be a major factor if even a factor at all. It takes a lot of phase shift to cause audible group delay at higher frequencies.
Physically "group delay" means that certain portions of the frequency response arrive later in time than others. Phase distortion and group dealy are basically the same thing only at dramatically different scales of the effect. It takes many many many cycles of phase shift at high frequencies to cause even a ms of group delay. Yes, zero phase change means no group delay, but the point is that it actually takes a lot of phase shift to even come close to something that is audible. So much so that to talk about it as phase is rather pointless and thats why the concept of group delay is used.
I've always been a fan of the sawtooth wave demonstration. You can't tell the difference between a sawtooth and its reverse. They have the same spectral content but have different phase.
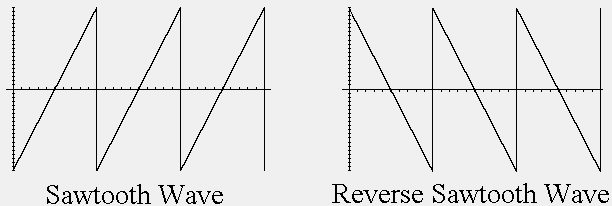
There is some reason to think that at very high power levels, one might detect a difference but this is actually because of non-linearities in the speaker. If it acts differently going one way than it does the other (creating even order harmonics as a symptom) then it may sound different, but that is because the spectral content changes.
As for detecting just the phase, try the sawtooth test. Find a signal generator capable of generating a sawtooth and its reverse. Flip between the two and listen, you may be surprised. At moderate power levels (before non-linearity becomes extreme), you can't tell the difference between a sawtooth and a reverse sawtooth. Kind of one of those little known and less cared about facts in audio that kind of surprise you. One would think a sawtooth and reverse sawtooth would sound different, but they don't.
There is some reason to think that at very high power levels, one might detect a difference but this is actually because of non-linearities in the speaker. If it acts differently going one way than it does the other (creating even order harmonics as a symptom) then it may sound different, but that is because the spectral content changes.
As for detecting just the phase, try the sawtooth test. Find a signal generator capable of generating a sawtooth and its reverse. Flip between the two and listen, you may be surprised. At moderate power levels (before non-linearity becomes extreme), you can't tell the difference between a sawtooth and a reverse sawtooth. Kind of one of those little known and less cared about facts in audio that kind of surprise you. One would think a sawtooth and reverse sawtooth would sound different, but they don't.
The Manger transducer (MSW) can reproduce a decent squarewave over a limited frequency range so can the Quad ESL63 allthough Peter Walker always stated that this gives no audible benefits (some headphones can do that too so there is an affordable source awailable to everyone that whould like to listen to a time coherent system albeit loosing the "natural" HRTF). Normal electrostatics can not do that because of combfiltering effects. In the extrem nearfield it works but at the listening seat signals of the same frequency reach the ear with different timedelays.
So a transducer with good squarwave reproduction needs to be an idialised pointsource.
Any passive solution will show considarable lobing effects and when you do not listen in the extrem nearfield a lot of signal will reach the ear from the difuse field that is not time coherent and coloured in tonal balance.
no wonder that speakers with a 6dB passive ACOUSTIC crossover sound very different
(better?)from speakers with a steeper crossover that have the same on axis response.
of cause you can try to make a coplanar-coincidental design and the speakers of the late Jim Thiel come close to that. Let me say that all timecoherent solutions i know of that are not digital (eg. analog) put considerable strain on the drivers so what you hear may simply be more 2nd and 3rd order distortion plus intermodulation that some people will actually prefer over a system that has technically speaking less dsitortion.
single ended tubes come to mind that can have a very "nice" even "adictive" sound.
at the University of Essex we build an active speaker in the beginning of the 90th that used FIR and IIR filters. it was a quite simple 2way design and there was a short review in HIFI News from Ken Kessler who was quite mesmerised by the soundquality.
We copied a forth order Linkwitz-Riley (ACOUSTICAL) with the IIR filters and used the FIR filters to adjust the phase, the groupdelay or whatever you call the timedomain artifacts. for me they are all the same. they have the same cause. the fist time in history (to my knowlege) we had a system with the same 3dimentional radiation pattern and distortion performane and where able to solely fokus on the "Time distortion".
it was extremely edjucating. when John k. will not slaughter me for my careless use of words to describe various elements of time phenomenons (we ones had a discussion about the ETC that left me looking like an idiot on the LSP-CAD forum) i will tell you more about what we learnd.
P.S: the Dunlavys and other similar constuctions achieve timecoherence only in a narrow HORIZONTAL window
So a transducer with good squarwave reproduction needs to be an idialised pointsource.
Any passive solution will show considarable lobing effects and when you do not listen in the extrem nearfield a lot of signal will reach the ear from the difuse field that is not time coherent and coloured in tonal balance.
no wonder that speakers with a 6dB passive ACOUSTIC crossover sound very different
(better?)from speakers with a steeper crossover that have the same on axis response.
of cause you can try to make a coplanar-coincidental design and the speakers of the late Jim Thiel come close to that. Let me say that all timecoherent solutions i know of that are not digital (eg. analog) put considerable strain on the drivers so what you hear may simply be more 2nd and 3rd order distortion plus intermodulation that some people will actually prefer over a system that has technically speaking less dsitortion.
single ended tubes come to mind that can have a very "nice" even "adictive" sound.
at the University of Essex we build an active speaker in the beginning of the 90th that used FIR and IIR filters. it was a quite simple 2way design and there was a short review in HIFI News from Ken Kessler who was quite mesmerised by the soundquality.
We copied a forth order Linkwitz-Riley (ACOUSTICAL) with the IIR filters and used the FIR filters to adjust the phase, the groupdelay or whatever you call the timedomain artifacts. for me they are all the same. they have the same cause. the fist time in history (to my knowlege) we had a system with the same 3dimentional radiation pattern and distortion performane and where able to solely fokus on the "Time distortion".
it was extremely edjucating. when John k. will not slaughter me for my careless use of words to describe various elements of time phenomenons (we ones had a discussion about the ETC that left me looking like an idiot on the LSP-CAD forum) i will tell you more about what we learnd.
P.S: the Dunlavys and other similar constuctions achieve timecoherence only in a narrow HORIZONTAL window
😀
Not to worry, John K's a "pro's pro". Roughly the equivalent of getting "schooled" on solid-state amplifier design by Nelson Pass.
Nice to see you here Joachim. 😉
Here is one of the better written articles on phase/time vs. intensity (spl differences) with respect to localization cues:
Physics Today On The Web - Cover Story
It's worth reading several times to get a better grasp of the information (for newcomers to this topic), but for the most part it's quite well written and fairly easy to read as a result (..at least when compared to other resources).
Basic synopsis:
Intensity differences are most important higher in freq.. say 1.5 kHz up.
Time differences (i.e. group delay) induced from phase shifting are most important below 1 kHz.
However *both* are somewhat over-broad generalizations.
For instance Earl suggested that phase-induced timing errors at higher freq.s require a great deal of error to be at all audible (in that the amount of phase rotation at these higher freq.s results in a comparatively low time delay), however note the following quote from this article (that specifically references time delay at higher freq.s):
"One might imagine that the network of delay lines and coincidence detectors described in the box vanishes at frequencies greater than about 1500 Hz. Such a model would be consistent with the results of pure-tone experiments, but it would be wrong. In fact, the binaural system can successfully register an ITD that occurs at a high frequency such as 4000 Hz, if the signal is modulated. The modulation, in turn, must have a rate that is less than about 1000 Hz. ."
So even at these higher freq.s for time/phase it's a matter of "it depends on..".
In fact, though not stated, a "read between the lines" message from this article is:
"..we really don't know much about this, further research is necessary."
So if you find someone making a definitive statement on listener *perception*, then well - it might be best to accept their statement as their *belief*, rather than as fact. (..though perhaps with a very good reason for their belief.)
Physics Today On The Web - Cover Story
It's worth reading several times to get a better grasp of the information (for newcomers to this topic), but for the most part it's quite well written and fairly easy to read as a result (..at least when compared to other resources).
Basic synopsis:
Intensity differences are most important higher in freq.. say 1.5 kHz up.
Time differences (i.e. group delay) induced from phase shifting are most important below 1 kHz.
However *both* are somewhat over-broad generalizations.
For instance Earl suggested that phase-induced timing errors at higher freq.s require a great deal of error to be at all audible (in that the amount of phase rotation at these higher freq.s results in a comparatively low time delay), however note the following quote from this article (that specifically references time delay at higher freq.s):
"One might imagine that the network of delay lines and coincidence detectors described in the box vanishes at frequencies greater than about 1500 Hz. Such a model would be consistent with the results of pure-tone experiments, but it would be wrong. In fact, the binaural system can successfully register an ITD that occurs at a high frequency such as 4000 Hz, if the signal is modulated. The modulation, in turn, must have a rate that is less than about 1000 Hz. ."
So even at these higher freq.s for time/phase it's a matter of "it depends on..".
In fact, though not stated, a "read between the lines" message from this article is:
"..we really don't know much about this, further research is necessary."
So if you find someone making a definitive statement on listener *perception*, then well - it might be best to accept their statement as their *belief*, rather than as fact. (..though perhaps with a very good reason for their belief.)
Last edited:
The use of DSP makes the design of TP speaker systems fairly easy. There are several approaches which can be used. For example, a typical speaker with passive crossover can make use of DSP preprocessing to linearize the system phase. This is useful because any speaker can be transformed to a linear phase, TP system while retaining the same crossover characteristics: roll off slope, polar response, etc. DSP can also be used to design linear phase, active crossovers from the get go. As Joachim pointed out (good to hear from you), the starting point can be a standard LRx crossover which is then linearized, or linear phase crossovers which have LRx amplitude and be used. However, the problem with any of these DSP approaches is that they all introduce pre-ringing in the high pass section. This may result in audible artifacts, particularly in the off axis response of system with non-coincident drivers.
Only if minimum phase HP and LP filters are used can this pre-ringing be avoided. MP filters which yield TP response can be generates which have higher slopes but these all have potential problems with polar response and off axis response peaking. Some of these effects can be overcome with good MTM type designs.
Only if minimum phase HP and LP filters are used can this pre-ringing be avoided. MP filters which yield TP response can be generates which have higher slopes but these all have potential problems with polar response and off axis response peaking. Some of these effects can be overcome with good MTM type designs.
Hello,
The square waves for the Maverick have a 1000Hz frequency and a 1 milliseconde period. Until 20kHz such quare waves only contain 10 frequency components which are odd multiple of 1000Hz (1kHz, 3kHz, 5kHz, 7kHz, 9kHz, 11kHz, 13kHz, 15kHz, 17kHz and 19kHz)
Things will be different if the measurement was done on 10Hz or 100Hz square waves...
Best regards from Paris, France
Jean-Michel Le Cléac'h
The square waves for the Maverick have a 1000Hz frequency and a 1 milliseconde period. Until 20kHz such quare waves only contain 10 frequency components which are odd multiple of 1000Hz (1kHz, 3kHz, 5kHz, 7kHz, 9kHz, 11kHz, 13kHz, 15kHz, 17kHz and 19kHz)
Things will be different if the measurement was done on 10Hz or 100Hz square waves...
Best regards from Paris, France
Jean-Michel Le Cléac'h
A quick mental test as to the "saw tooth" test. Look care fully at the wave forms. Reversing the sawtooth is exactly the same as reversing the phase of the speaker. i.e. you are doing the same thing as reversing the absolute phase of the speaker. Absolute phase is another can of worms which has generated a lot of rhetoric good and bad. So you are not really listening to the nonlinearities of the speaker, but more to a transient which is either absolutely positive or negative.I've always been a fan of the sawtooth wave demonstration. You can't tell the difference between a sawtooth and its reverse. They have the same spectral content but have different phase.
There is some reason to think that at very high power levels, one might detect a difference but this is actually because of non-linearities in the speaker. If it acts differently going one way than it does the other (creating even order harmonics as a symptom) then it may sound different, but that is because the spectral content changes.
As for detecting just the phase, try the sawtooth test. Find a signal generator capable of generating a sawtooth and its reverse. Flip between the two and listen, you may be surprised. At moderate power levels (before non-linearity becomes extreme), you can't tell the difference between a sawtooth and a reverse sawtooth. Kind of one of those little known and less cared about facts in audio that kind of surprise you. One would think a sawtooth and reverse sawtooth would sound different, but they don't.
As is so typical, you misquoted me. I said that PHASE errors at high frequencies could not be a problem, NOT that time errors (group delay) are not a problem. There is a very big difference. Time errors are clearly a problem and if you look at anything that I have written (and read it clearly) you will see that I have always asserted that. But phase errors such that a square wave is recreated are not meaningfull until they reach the level of group delay of a ms or so.
Thank you John K. for the nice words.
In my book IIR filters can be made to mimmic passive solutions.
we went no steeper at essex then 4th order L/R exactly out of the resons John K. hinted at : pre ringing and out of axis lobing.
in fact the finished speaker had quite a spectacular linear off axis response this due to the fact that we used a quite low crossover frequency and the property of the L/R that the drivers are in phase (relative to each other) over the whole frequency range.
In my book IIR filters can be made to mimmic passive solutions.
we went no steeper at essex then 4th order L/R exactly out of the resons John K. hinted at : pre ringing and out of axis lobing.
in fact the finished speaker had quite a spectacular linear off axis response this due to the fact that we used a quite low crossover frequency and the property of the L/R that the drivers are in phase (relative to each other) over the whole frequency range.
- Status
- Not open for further replies.