Hello,
Mostly ignorant of speakers rules ,white hair.
In the picture is what i build for home use.
Three separate boxes because this would allow new variants.
They need to be glued, but I'm not sure even if it doesn't sound bad .

Speakers Ciare HWB200-8 ,Visaton w130s,Monacor DT25N.
Simple filter (first and second order (?)) designed with some help with Xsim and FPGraphTracer.
Bass box internal dimensions 61.6x25x35cm, Vnet=51.5L(WinISD), port Dv7.2cm Lv15cm double front panel and two transverse reinforcements.

Please ignore the high standards you have for your works and give me some tips .
What can be done better,bass box dimensions ratio ,port and speaker location...
Thank you and sorry for any mistakes, it's google translate.

Over the years I've analized / modded / built a number of onboard bass preamps, for some of which there isn't much info out there, and I thought it would be nice to share all the info I have in a single thread. As I go along I'll update this with an index to the relevant posts. I'll also discuss some general topics such as opamp choice (post #2, post #27 and some suggestions for SMD opamps by @Passinwind in post #23) and pickup loading (post #3). These are some of the preamps I'll cover, in no particular order:

- A DIY 2-band Baxandall (post #4) I designed and made for a friend's Warmoth Jazz Bass

- Mighty Mite MM114 (post #6, no longer produced, see page 3 of this catalogue), it came in a Tobias Toby Deluxe 5 I bought back in 2001. An opamp-based, 2-band Baxandall eq with a couple of unusual twists

- Seymour Duncan STC-2P (post #8) and STC-2ASB (the Steve Bailey version, post #9), used in two Warmoth builds. Both are 2-band eq's that use opamps and transistor-based gyrators that lend themselves to many interesting mods (post #12 ff)
Edit 4-Nov-24: There was a small mistake in the previous posts, corrected schematics and sim files in post #10, plus PCB component layout and wiring diagram.

- An analysis of the 2-band Stingray preamp (post #16) and a DIY version based on it (post #17), significantly modded to get a more uniform response and to be able to use standard, easy to find pots

- Info about the 3-band Stingray preamp (post #20) for completeness (I have no experience with it) and possible mods (post #28)

Comments and additions always welcome.

Edit: the attached onboardbass.txt file contains the opamp and transistor models required for some of the simulation files posted below.

Want to use 6B4G as output tube in a SE amp with Ia 45mA. 2A3 is said to have Ua max 300V, but the specs for 6B4G says 325V with fixed bias AB at 40mA. Anyone who have tried 325V?

Looking for an Amp Camp Amp Mini amplifier or kit. I know I can buy a kit in de diyaudio store but there are probably a lot of them out there that are unused or not even build yet so maybe I can give it a second life. Preferably in europe due to delivery costs and import taxes.

Hi,

Does anyone know where can we buy toroidal transformers in Mumbai ? I have contacted one person BE Torodial Transformer but he doesn't communicate properly. Can anyone please let me know anyone else who manufactures transformers?

It would be greatly appreciated if someone could tell me whether the following well-known audio site from Phoenix AZ is still operating?

alan m. kafton / audio excellence az, inc
940 east cavalier drive
phoenix, AZ 85014-1912 USA
602-277-3737

I've been trying to order his Ground Breaker Adaptor Set for my Audiodharma Cable Cooker but have yet to receive any response despite three emails
(https://www.thecablecooker.com/order/ ) and unable to get through by phone.


Many thanks.

I have 2 pairs of Siemens D3A and Phico Type 26 that I planned to build something but never got time to do.
The D3A were bought NOS, used for less than 10 hours. The Phico 26 were bought tested NOS but I still haven't got them used.

Asking $130 including shipping worldwide for both pairs. PP fee is not included though.

I'm wondering if anyone here has actually built/designed a power conditioner. I'm asking because I suspect my main systems have less-than-optimal conditions due to switching power supplies, class D amps, and computers being part of the system.

The prices I see on the ones which look like good quality are sky high. Are they terribly complicated to build?

Hi Guys,

If an amp is with a FET (mosfet or jfet) input stage, can I omit the DC-blocking feedback cap?
I need real world experience. As you know, in the simulation, everything is perfect.

Thanks.

I'm starting this thread to talk about an interesting and new method for "removing" group delay from a continuous audio signal using reverse-IIR filtering.

Background: When you perform "analog style" filtering on a signal, that filter does not output all frequencies at the same time. Instead, frequencies emerge from the filter at different times. This is a consequence of what the filter is doing in the frequency domain (e.g. to the frequency response) - the filter automatically produces non-linear phase changes to the output signal. The result is a distortion of the time-domain waveform, because the appearance in time of various passed frequency components has been altered compared to the input. This sort of phase-domain distortion does not in any way change the magnitude of the frequency component (the frequency response) but the signal in the time domain may look badly distorted. This effect is called by different names, including phase distortion and group delay distortion. When the distortion grows large enough, it is possible to perceive a change to the "tone" of the signal. At lower levels it becomes imperceptable/inaudible. in general, the steeper the filter the worse the group delay distortion and this puts some limits on how steep of a filter we can use for a loudspeaker crossover. With FIR filtering, the situation is different. Phase and amplitude of the filter are independent of each other and this means it is possible to choose the phase to be linear (meaning the group delay is flat). Until now, FIR processing was essentially (to the best of my knowledge) the only practical way to implement a filter with a linear phase response.

More Background: Forward-Backward IIR processing. Someone realized that if you had some finite quantity of sampled audio you could process it first in the normal "forward" direction, and then also in the "backwards" direction. The filter's magnitude changes are applied twice. But the changes in the phase of the signal are exactly reversed, undone, and set back to zero in the "reverse" pass of the filter. What is happening is that the time shift of a given frequency that occurs in the forward direction is exactly equal to the time shft from the reverse pass, but these are opposite in their time "direction" and so they cancel. The result is zero phase distortion, zilch, nada! Let's do it says the crowd. Ah, but implementing this is not so simple. In the forward pass the ringing tail of the signal requires some time to "die down" This extends the duration of the original signal by the length of the tail. This tail must also be processed in the reverse pass in order for it to be brought back in time to its original "place". But if you have a continuous signal, things get tricky. There have been attempts at overlap-and-add methods to process chunks of a continuous signal and then sort of stitch them together but this typically leads to end effects and other problems, and the algorithm is a bit messy.

To the rescue and something that I belive is completely novel is the work by Martin Vicanek that is described in his whitepaper "A New Reverse IIR Filtering Algorithm":
https://www.vicanek.de/articles/ReverseIIR.pdf
I will not get into the gory details of the algorithm too much here. However, in the whitepaper Martin describes a way to take the "Infinite Impulse Response" of the IIR filter, truncate it to make it an FIR response, and then reverse the FIR as blocks in order to reverse the poles of the filter. It's frankly some brilliant work that completely eliminates the need for block processing. The only inputs to the algorithm are previous INPUT samples. There is no longer the feedback from output samples because of the re-formulation of the IIR as an FIR (which is then reversed). This allows for continuous "forward only" processing of the audio signal, and this can go on indefinitely. Best of all, the number of operations required for the processing is much less than the equivalent FIR and latency is much less than reverse-IIR block processing methods.

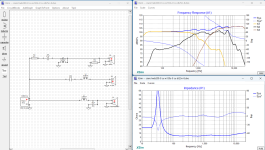
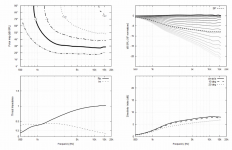
So, how does this help with loudspeaker group delay? While reading Martin's whitepaper I recalled that the group delay from the summed outputs of an Nth order crossover (the sum of the lowpass and highpass filters that make up the crossover) is the same as the group delay from an all-pass filter of order N/2. An example of this is a 4th order Linkwitz-Riley crossover, which is constructed from two second order Butterworth filter (each having the same pole frequency and Q=0.707) run in series. The LR4 has the EXACT same group delay as a second order allpass filter with the same Fc and Q. So, to make a linear phase LR4 crossover we can implement the allpass response, "in reverse" via the RIIR filter, upstream of the crossover to "pre-distort" the phase of the signal so that after it passes through the LR4 and undergoes an "in air" summation the phase remains unchanged.

The applicability of this technique is very broad. This is because we only need to find the group delay response of the loudspeaker that results from the crossover filters and other sources of delay, construct approximately the same group delay response using only all-pass filters, and then apply those all-pass filters in reverse using the RIIR filter. It doesn't matter what order the crossover may be or what the source of the group delay, as long as you can model or measure it you can cancel most or all of it depending on how close a match you can get via allpass filters. My recent effort to do some group delaey audibility testing, as well as what has been repoted in the literature about group delay, indicates that group delay does not need to be zero but only below some threshold to remain inaudible because human hearing is just not all that sensitive to it. But what (to me) is interesting as someone interested in new frontiers in crossover design, is that filters that previous had too high of a group delay response because they were "very steep" can now be corrected to have as low of a group delay as you wish. This starts to blur the lines between IIR and FIR processing and what each type can accompllish, and I find that pretty interesting stuff.

So, are there any downsides? Well, not really but there is a consequence to the RIIR algorithm: latency. When I described how the algorithm works, above, I mentioned that the IIR impulse response is truncated to become an FIR filter. This truncation introduces error because you are at some point setting the remaining part of the impulse "tail" to zero. This is a source of error or noise in the output signal. The more of the tail you retain, the lower is the added "noise" signal. Luckily Martin provides a way to determine how much of the tail needs to be retained when given some signal to noise ratio that is desired. Also, because the tails from poles located at lower frequencies last longer than for higher frequencies, RIIR filtering for filters with lower pole frequencies requires increasing latency. But luckily the tail decays exponentially, and so the latency is not too severe. In a test trial I ran a 1kHz 2nd order allpass as an RIIR filter. This required 128 samples of latency at 96kHz, which is a latency of 1.33 milliseconds. It's a small price to pay indeed.

I have created LADSPA plugins that implement the RIIR algorithm for first and second order allpass filters. These can be used for phase and group delay equalization and linearization. As of 27SEPT2024 these are available for download at my LADSPA page:
http://audio.claub.net/LADSPA-plugins.html

I will post some follow up information including some more specific examples soon. For now I thought I would put this out there to start a discussion and raise awareness of this processing algorithm.

Hi

I’d like to build the popular Manzanita Open Baffle but can’t find the required 20mH, 16 AWG inductor for the 6dB Low pass filter, it’s back ordered in most places.
Please let me know if you have a pair available. Picture shown below


Thanks
Eric

Hello.

I have been working with many different electronic systems my whole life, career and hobbies included.
My favourite is anything to do with audio and that is why I am here. Hoping to gain knowledge from other like minded people.

Hello to all. My name is Koulle. I have been tasked with providing a plan to turn some Volvo Dynaudio 4ohm car speakers into "world class" bookshelf speakers. I have been reading J. D'Appolito's "Testing Loudspeakers", wondering if I could find a handle to create a flow chart to the dark art of speaker building with ones own drivers. Can't get off first base. So here I am posting a short intro and hoping that I may borrow valuable information from you. So, thank you in advance. Suggestions as where to begin in terms of where to post my first question would be appreciated.

I have a Dynaco Pas 3, looking at different options on replacing the electrolytics. My question is, if using film capacitors can I use lower value compedance than what the specifications call for and still get good performance?

I just picked up a pair, also got the tops. Used to have the SP1 variant of these years ago.

I’ve seen some posts from people stating the Klipsch 33, 43 or the Emminence 15c is the way to go in these bins.

I’m using these in my workshop with the occasional yard parties with a pair of Dynaco Mark 3’s.

Does anyone have any experience with these and can recommend a driver for them as well as a complimenting horn driver(s) for a passive 2 or 3 way setup?

Hi Guys,

I have a 40 year Miller & Kreisel Volkswoofer III that I need to do some minor repairs on.

I need to replace the gain pot and the phase switch.

Fairly straight forward but I can't find where in the schematic the phase switch is located.

It could be that I am blind however I cannot find a switch anywhere in this schematic.

I originally posted this at ASR -> https://www.audiosciencereview.com/...23-i2s-dacs-diyinhk-es9016-dac-opa1612.47265/ but figured I might have more luck here given the nature of these items. I've also lowered all the prices from the original listing. All prices are shipped to US.

1) Ian Canada McFIFO / McDual XO - $150 shipped
Originally purchased for use as a clock buffer for a miniSHARC based 8 channel DSP AES output project. It accepts multichannel I2S and will buffer / reclock input data using oscillators on the McDual XO. In addition it provides 4 MCLK, BCLK and LRCLK outputs which makes interfacing with stereo I2S input boards very easy. Comes with the stock oscillators and will include 24.576 MHz and 49.152 MHz NDK SDAs on DIP14 adapters. If you are interested in interfacing with the I2S to SPDIF/AES boards I have in this listing and I can thrown in some U.FL to pin adapters that work great.



2) WM8804 I2S to BNC SPDIF Output Boards - $15 shipped (first one is $15, if you would like more each additional board is $10)
I originally had five of these, I now have three. These convert I2S to SPDIF input and take 5 V power. Made in a form factor that is plug and play with Amanero they also work great for other general projects. They are reasonably sized and work well. If you want to adapter the pin header to U.FL connections these Ian Canada adapters for the Buffalo III DAC work perfectly.



3) WM8804 I2S to AES Output Boards - $15 shipped (first one is $15, if you would like more each additional board is $10)
I originally had five of these, I now have four. These convert I2S to SPDIF input and take 5 V power. Made in a form factor that is plug and play with Amanero they also work great for other general projects. They are reasonably sized and work well. If you want to adapter the pin header to U.FL connections these Ian Canada adapters for the Buffalo III DAC work perfectly.



4) AK4118 SPDIF to I2S Board - $20 shipped
This board takes TOSLINK or SPDIF and outputs I2S. It has been discontinued for sometime due to the AKM fire but is a great way to add SPDIF input to I2S devices. It runs on 5 V power.



5) OPA1612 op amps on DIP 8 adapters - $5 shipped (or buy all of them for $50 shipped)
I have fourteen of these. Not much to say other than these are low noise and distortion and easy to use in DIP 8 sockets.



Michael

Hey Folks,
I've been hooked on the idea of making a WAW for a while. I've also been heavily inspired by xrk & bushmeisters bookshelf synergy thread and love the look of the results they have gotten from the SB 2.5" fullrange.

As it stands I don't believe I have the technical knowledge or physical skills to create a MEH, so I'd like to buy a horn, print adapters and create a WAW setup to begin with. One day I could move to making a MEH.
I've been considering a number of different fullrange 2"-4" drivers and would like to test multiple over time. I'd start with the SB 2.5" and adapter xrk designed in the bookshelf thread.

Please note, my primary goal from horn/waveguide loading the full range is controlled dispersion. Not increasing the SPL of the driver.

Why a WAW/ Fullranger, instead of a compression driver? I want to cross as low as possible in true WAW/Fullrange philosphy of avoiding crossovers in the main audio spectrum. But I also want more bass than can be found from full rangers (WAW), with better dispersion thus trying to horn load these little guys. Compression drivers that reach 300-400hz and have a good top end are not cheap in the slightest!

I am considering the two following horns after a fair amount of research and would love some external thoughts:

Eighteen Sound XT1464 horn https://www.eighteensound.it/en/products/horn/1-4/0/XT1464
for 60x 50 degree CD with 500hz loading.

RCF HF950 https://en.toutlehautparleur.com/media/catalog/product/datasheet/rcf/HF950.pdf
for 90x 50degree CD with 400hz loading.

Is there a reason you wouldn't choose the HF950 besides size?
Are there any other affordable, CD, low crossed, 1.4" commercially available horns you can think of?
Am I just nuts and should stay with a more traditional WAW design?

The reason I am starting a different thread is that this build isn't constrained by size like xrk & bushmeisters discussion is, it isn't immediately a MEH and I don't want to muddy their waters.

As regards to the overall WAW design, I’d see the primary goals as:
<500hz crossover.
1/4 wavelength distance CtC spacing
Good directivity to 10k+ hz
In room Bass extension to 35hz.

Nice to have goals:
<300hz crossover
85+ db total speaker sensitivity
Passive crossover option - unlikely.
Time aligned
Low THD for both drivers
Flexible in room positioning requirements

Would love to hear your thoughts,

scored a pair of gee jay cabinets a couple of years ago. they have a sliding wood panel to adjust the eq level. i have some newer model ev sp 12 b's in them. would love to add some sparkle, can I bi-wire some bookshelves to them to keep it simple, or is that going to ruin everything?

I just recently noticed a strange behavior on my X250.8 meter. With no input the meter has a small rhythmic "twitch". It literally looks like my amp has a beating heart. In the past the meter has only shown movement when pushing the amp from class A to AB. Does anyone know if this is cause for concern... as I said there is NO input and the wall voltage is a constant 120.6 volts.
Thanks,
Tom

Hi!

For this project I'll be using 40 pcs of micro speaker (102dB@10cm) spaced at 9.1mm C-t-C to emulate a ribbon.

The "ribbon" will be mounted to the throat of a custom ATH4 horn flare. I will use an 8PR200 for bass.

To improve the vertical wavefront / directivity I will add active shading to each speaker or group of speakers.

Each micro speaker will be driven by its own MAX9718A amplifier.
https://www.mouser.co.uk/ProductDetail/Maxim-Integrated/MAX9718AETB+T?qs=1THa7WoU59FvOsgrnnj7bg==

It will be straight forward to taper the levels vertically as the MAX9718A exposes adjustable gain.

For delay I may try wrapping the appropriate allpass/bandpass around the MAX9718A or alternatively use a few LME49721.

More to follow.




polars



horiz at 45deg no shading



vert at 5deg no shading


test board

Information outside of Japan is scarce, but I believe these were YL’s TOTL high frequency driver / tweeter. Very rare to find one in working condition, let alone a pair.

$2,000 net to me, shipping only in the USA for now.

Found the site through a few random searches and there were some great threads I still have some questions on.
Large fan of 80s-90's rock and have been known to cycle through hardware on a personal quest for things I think sound better.
Looking forward to reading up on other peoples projects and trials with varied hardware.

Creative Inspire T6060 P.C.B.
I needed to repair a humming system,
so I drew a board with parts,
since I couldn't find a diagram anywhere

Hey there,
I cant find a clear answer to this question…. Do transistors (if stored properly) degrade while sitting on the shelf? I often find new transistors to have a too high hfe for repair jobs on old gear. Is it a safe bet to replace them with nos transistors? Or am i better off to buy new production? Im talking silizium transistors - not germanium.

Cheers

I have a pair of each of Faital Pro 8hx150 coaxials and 18fh500 woofers. I have been thinking about putting them back to back magnets facing each other, nude open baffle at ear height. Delay can be added on DSP. Crossover around 300hz ish. Can you think of any major problems?

Been experimenting with one of these - https://www.ebay.co.uk/itm/265099568381 - it actually sounds pretty reasonable.

A big part of the appeal was it should work with a wide range of PSUs and doesn't need a dual rail supply, I was hoping to power this and a cheap class D amp off the same PSU - I was thinking a generic 18v laptop supply to keep costs down.

I've found that it's hum free with my bench PSU but that it has a slight hum with the laptop supply. Initially I thought this was power supply noise, but using the laptop supply I tried running a wire from ground on the phono board to the (mains earthed) case of the bench supply - the hum went away.

The turntable I'm using is not earthed to the mains either, so with the laptop supply earth is floating.

Any ideas on how to get this working quietly without a mains earth? I wonder if a similar switch mode power supply with a 3 pin (earthed) mains would behave differently?

I'm hoping this gets someones attention. I still an unable to get right channel to come on. If anyone been following this fiasco then they don't need a recap, but for thoses who just checked in I will try to bring you up to date. A couple of weeks ago I decided to take my Krell KSA300-s out of a 3 year storage. This has been stored in a climate controlled building. I'm not the original owner, but I had used it for 5-6 years with no problem.
Anyway I got it set up and no right channel. No lights (led's for that side were on). Left side fine. So, I took it apart and found several issues with a previous repair. I fixed those and turned it on again, nothing. I decided to go in deep and found a couple of other problems so I fixed those.
To try and keep down the total times I took this apart I check every active component on that side. The only thing I haven't check were some timer ic's that appear to be used in the auto-bias circuit. Unfortunately the auto-bias circuit is the only thing I don't have a schematic for (and it appears no one else does outside of Krell who appears to be out of business).
I'm in the dark now and asking anyone that might have some insight to this problem to please come forward. I'm very close to putting it to the side and moving on. So, there you go.
I have attached some schematics that would be helpful.
Thanks,
John

I have built a pair of towers using vintage drivers I salvaged from beat EPI-400 speakers. They turned out really nice and sound pretty good overall, but bass is a little weak/undefined at lower frequencies. I suspect they could benefit from a little effort at fine tuning them, but I would like to take semi-educated guesses at what might be best to try. Hoping to pick the low hanging fruit first.

Relevant clues that some modifications are necessary:

• Woofers bounce a at high volume.
• There is fairly significant cabinet vibration while they're playing.

Some relevant information:

• These are 6" woofers and they unfortunately do not have any thiele/small information published about them.
• EPI didn't build any double 6" woofer speakers so I went through some extremely exact math (wink wink) to determine internal volume. I determined the percentage change in volume between a single 8" woofer EPI two-way to a double 8" woofer EPI two-way, and applied the same percentage change to single 6" woofer model from their line-up. End result was a 3600 cu. in. enclosure before bracing, I think ~3400 after. For reference the quadruple 6" woofer EPI-400 these came out of was ~5000 cu. in.
• The speakers are built out of 3/4" MDF, have internal bracing front-to-back and side-to-side, and are stuffed with fiberglass.
• The surrounds are original butyl surrounds. They are not that particularly stiff or cracked.
• Polarity has been double and triple checked
• I have messed around with placement some as well. They do better against the wall than they did away from the wall (like in the below picture), I've also found they're fairly directional speakers. Bass is definitely improved when you're dead center and near the back wall.

Things I've thought to try, but am not sure which might be most impactful

• Decrease internal volume
• Increase quantity of bracing, though would have to get creative with this since their are fully veneered now
• increase/decrease quantity of stuffing. Amount/compactness of fiberglass is in line with other sealed enclosures I've seen
• New surrounds

Does anybody have thoughts as to what would be best to try? Thanks!

I believe someone here has rewired his Graham 1.5 arm. I want to do this with my Graham 1.5T. I understand that to gain access to the wiring, heat from a heat gun must be applied to loosen the epoxy sealing the arm. My question is, what areas of the arm are epoxied? I do see epoxy in the area where the leads exit the arm near the cartridge. Is the arm epoxied near the end where the arm attaches to the mounting? Thanks.

Hello. Hoping you more-educated &/or experienced folks can help me out with figuring out what inductor value are in these Totem Hawks. They're not marked, so I disconnected them & took a reading with an LCR tester (see pic), but the reading doesn't make sense. The woofer is supposed to be 6 ohms, the crossover frequency is supposed to be 2500Hz, but these numbers just aren't adding up. I'm sure I'm missing something & could use some guidance. Measurement shown. Please & thank you in advance.

...

Hi! I have built a MOSFet cap multiplier to filter valve amp B+. Here's the schematic:

Real life DC behaviour on the bench matches the simulation closely.
I have a meter on the load resistor and a meter on the output of the PSU powering it. It is an old unit with an indirectly heated full wave rectifier, so comes up slowly.
The cap multiplier has the typical slow startup from the time it takes for C1 to charge. At the point where that is nearly finished and Vin starts to drop, there is a click sound to be heard from the cap multiplier and Vin jumps up to 1kV for a moment. Unloaded Vout of the psu is 510V, under load 484.
Do any of you have an idea where that spike is coming from and how to suppress it?

Thanks for any useful input.

Hi everyone I'm currently in the process of building myself a sound system for my home. I'm currently in the process of choosing what drivers I'm going to use for this build but I'm not entirely sure what drivers to choose.

I plan on having 2 bookshelf speakers for left and right, 2 surround and a subwoofer. For the bookshelf I wasnt sure whether to make a 2 or 3 way speaker. I have already purchased the epique e180he-44 speakers I saw great reviews for this speaker but I'm not to sure what speakers I should pair with this speaker, I've been told the e180he-44 is best in a 2 way but I think a 3 way must be better to achieve better quality of sound and a wider frequency range.

Please could you give me some advice as im pretty new to this I just want some decent drivers to pair with what I have. For the crossover I'm getting one custom made for when bookshelf speakers once they're made.

Thanks

I am in the final stages of building a pair of Monoblock ( LL7903/1:8 to a 46 to a LL1671/30mA to a 300B to LL1664/80mA)
I've got all the PSU dialed in and was reading some of the articles from Ale Moglia of how he switched to the 47 for a bit more gain given his 2v input so wanted to check my gain by the stages.

I have a 4V input from the DAC (SMSL su-10) so the 46 would see ~30V on the grid. I almost went to turn the amp on and realized that the Rk on the 46 is at 17.7V. Should this be 32V ish? should I just do a B- supply to this or do a Rk with a higher value to give me the 32 ish V on the cathode?
Obviously the B+ would have to change to around 240@30mA if using the -30 curve.

With the 4V into the LL7903 in 1:8 it yields the 30V and the mu of the 46 is 5.6 which should translate to 168V swing. The max per the LL1671 on the secondary is 130V rms. Will this configuration drive the 300B too hard and the 1671 too hard as well? I have highly efficient speakers at 96db/w/m so I probably wont be cranking it all the way up anyway but wanted to check everyone's thoughts here.

I trying to repair my function generator and having issues with a transistor replacement transistor is MJE371K. Of course cant find one of these, so I started checking for an
equivalent. However ever one I find is also out of production… can anyone help

We had a power cut last night, once it came back, everything turned on as normal... except my two DIY Hypex monoblocks.

Specifically, both SMPS1200A700 modules have stopped providing any DC power. There is no relay "click", nothing.

- The fuses are fine
- The current inflow thermistors are fine (I had to replace one of these before)
- The main capacitors are charging
- I've tried letting the main capacitors discharge fully before powering on again - no change
- I have checked on other power outlets - no change
- I have tested with and without NCORE modules hooked up

According to the HYPEX data sheet, the SMPS can be latched off if the NCORE module sees a fault, but this should be unlatched after capacitor discharge.

There is also the following in the datasheet, but no more details of how it works:
"The supply is triggered for normal operation or latched off in case of critical fault via in built-in actuators."

Does anyone have any ideas for common faults/diagnosis? The fact they both failed in the same way seems suspicious, and I really don't want to drop >400Eur on two new SMPS if it's just a fault-protection, then wait for the next power cut...

Hi all,

I have one of these nice DAC boards:

They say the analog supply voltage shall be +-12V. But AFAIK, the PCM1794A only sees the digital 5V supply voltage, while the maximum analog voltage is mainly determined by the op amps. So, if I'm using NE5532/34 op amps, +-17V should be safe.

Can anyone confirm this?

Thank you!

Hello! I am currently doing an ICEpower 50asx2 btl to repair. I would need the time of the C 201 times. Unfortunately, there is no plan for these modules. I hang a picture to which component I mean.

C 201 between Elko an Diodenbridge

I acquired these for parts but thet are weird. At the front is a 4" woofer with a tweeter and a port. To the rear is another 4" woofer & another port. The tuning frequency of the ports differ.

Can anybody follow JVC's thinking?

Afternoon,

I'm looking for anyone buying from the diyaudiostore who is keen to go halvsies on postage. I want some keratherm insulators and solder. Postage made me twitch at $63. Any other options people know of.

Thanks

Hello!
I'm still new to audio electronics and learning a lot as I go.

For context, I’m working on building my own USB microphone from scratch as a starting point for more complex personal projects. My current design is inspired by DIY Perks, but I’m designing my own preamp and power supply circuit. I’m working with a tight budget and limited access to specialized or hard-to-find components, so please keep that in mind.

Right now, I'm running into an issue with my power supply section of the circuit.


When the power supply is not connected to the rest of the circuit, it provides a stable +15V and -15V output. However, when I connect the preamp to the power supply, the voltage drops drastically to around 1.2-1.8V.

After testing, I discovered that when I directly supply the preamp with ±15V, it works perfectly. This suggests the issue might be related to the Darlington pair circuit.

Blue is micInput, Green is output (Power input connected to pre-amp) Red is output, Green is micInput (Direct ±15V connection)


Could you help me identify and resolve this problem? If there is anything else, don't be afrain to rag on me for that as well.

Thank you all in advance!

Selling 1x pair of A-875 line output transformers, excellent condition

17K:600 (150 split), 7ma

Originally designed for the 6SN7, but of course can be implemented for any tube that fits the specs, like a 76 for example

Asking 600€, will ship worldwide

Suno.ai can generate music from a prompt. Either with your lyrics or a full song. To me, it is amazing in the sense that sometimes it produces quite nice stereo "recordings". Certainly radio quality🙂

Hello.i need to replace the mundorf 2200uf 63v with 2200uf/80v.i have six first one modules and in one of them the caps failed after 8 years.
luckily it became noisy before it fail completely and destroy the module.
i would like to replace with 80-100v since the 63v is near the limit.
any recommendations?

Electret microphones offer a low-cost alternative to condenser microphones if the requirements are less demanding.
Are there similar electret planar loudspeakers around? Then we won't need dangerous high bias voltages...

hey all, in the never ending adventure to both have nice sound and WAF, i'd like to try to build a speaker for corner placement, which will mostly be behind a chair in the corner. This is for mono playback, so there's no second speaker, just one speaker in one corner. I'm currently listening to a linkwitz pluto, but although i like the sound the omni pattern and it works well with mono-playback, it really wants a closer listening position and i don't want to keep dragging the speaker out from the wall every time i want to listen.

The whole thing will use minidsp for crossovers/eq. Primary seating position is about 16 feet away from the corner (see attached poorly drawn room layout). Right now unless the Pluto is close (<9ft away or so), there's too many reflections going on in a bad way (expected but worse than i had envisioned).

so here's what i'm thinking to try to play well with the corner:
highs (>1250hz): B&C DE250-8 compression driver paired with either a HM17-25 or H6512 horn (horn and xover point to be decided upon testing/listening)
mids(300-1250hz): Dynavox LY302F 3.5" tucked right into the corner as close as i can get it
Lows (40-300hz): Dayton RSS210HO 8" woofer

see attached bad sketch of how i would arrange the drivers. view is at a 45deg section of the corner. I neither enjoy nor excel at woodworking, so i was hoping to just use the denovo knockdown cabinet for the 8" woofer. so all i'd have to build is a simple box to house the midrange. Unclear right now if i'd just mount the midrange box onto the wall, or have legs that go down to the woofer box.

I've seen Wayne's PI corner speakers and if i had the space i might just buy that. but they too big to pass the WAF test.

all thoughts, comments, criticisms, better ideas welcome! Thanks!!!!

Hello, I'm Peter and I want to make a custom mic from scratch. I don't really know what I'm doing, and I'm only equipted with some shaky electrical theory.

Wish me luck!

So, have a chance to get one of these for $50, anybody know anything about this amp? Is it the same league as Pyle, Crown, Carvin, QSC, etc? Is it worth the money, specs if any, will it do the rated wattage? Or is it a good door stop?

Thanks,

Hi,
Don't think I am a DIY person because I am a member here 🙂 I can do "some" stuff but not too much 🙂

So, I bought this DAC from someone knowing it was not powering up. The seller said he had no time to check and I took my chances thinking it could be an easy fix such as a bad fuse. I was like you know what I had a unit with an issue before and a fuse replacement solved the problem. Maybe this will be the same.

I put the appropriate fuse I hope because that's what it had in it, slow blow 3/8A (375mA).

WELL, THE UNIT POWERED UP, I pushed the buttons, they were all working, etc. two minutes later, I saw the fuse burned like red and then puff! The unit back to dead again 🙂

What could be the reason for working few minutes and then burn a fuse?

I have a friend who has all the tools to fix it (if fixable) but I thought let me ask here maybe it would help him pinpoint the problem.

For those of you in the US needing to add hand tools to your kit, I've been seeing a bunch of sales on Klein tools. Diagonals/linemans/wire stripper combo for $50 is a relative steal. There are other deals worth exploring as well. The big Milwaukee push to ride the Red Fan-boy wave, offering an ever increasing product line, plus the fact that quite a few tradesmen have been gravitating toward Knipex/Wiha/Wera tools, has apparently had a significant impact on the old guard.
That said, after decades of using Klein HT almost exclusively, I'm trying some Knipex pliers/Wiha screwdrivers and I'm impressed.
In any case, its a good time to snag a deal if you're in need. HTH somebody.
Cheers

Hi all, I would like to introduce myself. I am Peter from Belgium.
I am a hifi lover since I was a kid.
Special interest for diy speakers and especially magnetostatic ribbon speakers and other kind of line array setup's. I own a pair of Straethern Audio 60cm magnetostatic drivers, built in a 2-way system with Scan-speak 8" woofers.

Wanted - USB to I2S board to feed something like an AD1865 or similar.

Thinking Amanero or JL Sounds, but open to others.

I'm in London so would prefer easy postage to the UK. Andy

I have mounted the tonearm of an Akai AP-001 on my turntable. I placed a cartridge and headshell on the tonearm which are so heavy that the tonearm weight is almost at the end of the tonearm for the correct tracking weight. I read on a Lenco forum that Akai sold a separate additional weight for this (and similar) tonearms, encircled on this image. Does anybody happen to have this additional weight?

I am new to higher quality DAC's and need a recommendation as to the preferred interface?

Hi,

I plan on building Troels Gravesen “The Loudspeaker 3” to replace my Audio Technology 3WC sometime in the new year. Its an itch I need to scratch.

I have limited woodworking / soldering skills (practical skills in general!) and would really appreciate if any of you could share any useful tips with me.

My intention is to use either 21mm or 24mm birch ply and get the panel sizes cut to size with the driver holes CNC routered out by others and assemble the cabinets myself. I plan on staining the finish side of the panels before assembling (as Troels practices) and use a peg board to cable tie the crossover components to.

I’ve seen these square clamps to achieve the right angles are they suitable, or are there better versions to use?
https://www.ebay.co.uk/itm/39526735...=2047675&ssuid=&widget_ver=artemis&media=COPY

My existing speakers I have lined the inside with 5mm (10kg) barrier shield product and plan on doing the same again as I immediately noticed that the speaker / cabinet sounded quieter. Website with date sheet is: https://www.cmsdanskin.co.uk/indust...c-material-for-industrial-use-type-wb-epdmbs/

I was then going to use 25mm self-adhesive foam sound insulation to create a poor mans version of “No Rez”……do you think that would be beneficial?
https://www.ebay.co.uk/itm/14129530...ar=440412235067&widget_ver=artemis&media=COPY

I also found it hugely beneficial to stuff the cabinets with rockwool, so I plan to compare this to the wool roll included in the kit..

For the horn itself, I have read about people dampening the insider face of this, I was thinking of using a 2 / 3mm bitumen sheet and then using the 25mm foam insulation on top…..Is this a good idea?

I would appreciate any soldering tips….what is your opinion on using spade connectors for the drive unit connection? I remember trying to solder the speaker cable to the drive unit connectors and the pull from the magnets was insane, it did pull the iron towards the magnet a few times tbh and I struggled holding the wire still while the solder set….

Under my existing speakers, I am using industrial springs to isolate the speaker from the stand and was planning on doing the same again by using two steel flat plates, front and back that span across the speaker and go out the sides…
https://www.christiegrey.com/industrial/enclosed-spring-mountings/

I would really appreciate your thought and advice so this build can hopefully be a bit better than the last. Thank you

Hello everybody.
I am looking for the complete software for LinearX Lms, version 4.6, alternatively also 4.1 or 4.0 or even all versions.
The update setup on the physical Lab site does not work for my version.
I currently have the Dos, Linearx Lms 3.5 version only.
Please, I ask you for support.

My email is:

martincastrovincisystems@gmail.com

Thanks for helping me.

Hello,

My KRELL KAV280cd is faulty !
The problem :
- digital outputs, coax & optics are OK,
- analog outputs, coax & XLR, left & right are wholly
dead.

Power supply is OK : +/-18v +/-5v ...
Then, I suspect one issue on :
- digital filter board,
- or on DAC board

My problem, for understanding and repair :
- I have no schematics, no sm
Truly, I would appreciate if you could help me

Raymond
( pardon my English ! )

Hi all, I would like to introduce myself. I am Remco from Rotterdam, The Netherlands. I am an audio lover since long. Recently I have been spending quite some time on upgrading my Music Hall MMF 2.2 turntable. And this site is a great help in doing so.

.

Hi I'm currently in the process of building a home theatre sound system I came on here to learn a few new things about sound systems

I have a Sanusi BA-2000 that I like a lot that I have recapped and refurbished a bit but to me there is a perceivable lack high frequency content compared to other amps. It seems like this is a consensus among other owners. The stated specs say otherwise and that it's response is pretty much flat in the audio band. I was hoping to dive into the circuit a bit to try and find what part of the design could be affecting this. My initial thought is that there are some frequency / phase compensation circuits affecting this and perhaps they could be modified.

On the driver board, I'm looking at (guessing!) C03 is (33pf) is part of a low pass filter (maybe this value could be lowered to 22pf). C29 and 31 as miller compensation and C33 and C19 as low pass filter and compensation. Can adjusting the miller compensation caps have an effect in the audible spectrum? Also, could I lower the value of c33 and bleed off less high end? There also is a capacitor C55 that appears to be hanging off the feedback path as well.

I'm just taking wild guesses here so if there's any way to get to the bottom of why this amp seems to sound a bit dull and ways to change that, I'm all ears.

Hi there, I'm Andrew from Australia. I've come to building cabinets from PA and hifi. I'm not very far along in my journey but am always looking for good, clear sound.

The hum is likely induced electromagnetic coupling between transformers. Should also have strong 120 hz component. Good luck.

What's the general consensus on using mains filter capacitors (class X and class Y) between live and neutral, live and safety ground, and neutral and safety ground? I remember reading somewhere that this can cause more noise problems than it helps.

This device, FIIO R9, is the definition of frustrating. After three days I'm ready to send it back.

Who knows the exactly name of very high voltage booster capacitor manufacturer to the logo "db" (see attachement) ?

hi - quoting something i read - Since it's a figure-8 pattern, the two sides are 180 degrees out of phase - would this be true of ribbom mics ?

i get that a condenser has back to back out of phase diaphragms

Hi,
I lately got a pair of 15" gold but without the original crossover. The autoformers which were used in the crossovers are not easy to reach. I think the autoformers can be substituted with a fixed coil inductor. I therefore would like to ask if any member has done one before with this same situation. Or any recommendations/ comments are welcome.
Regards
Albert

Hi,

I have blown an IXTH12N100L linear MOSFET (1000V 12A 1.3Ohm 400 Watt TO247AD) today. It's used in a regulated linear high voltage power supply.

I cannot find them on stock with my usual suppliers and I'm unable to find a suitable alternative.

Any help finding this mosfet or an alternative is very much appreciated.

Regards, Gerrit

Hello! This is my first decent diy 2 way speaker project. Drivers are sb acoustics sb26adc in 8" waveguide and peerless hds 83089. They are still in progress so i post some measurements and more pictures and info here later.

Hello!

I have just got my hands on one of the old school cylindrical MF X DACs. It seems to lock on to any signal I plug into it from either a CD/Sonos/TV but the output is extremely low and a little distorted. I've tried coax, optical on all the above sources and on 2 different systems and the issue is the same every time. Any ideas what ,might be causing this or how I could resolve?

Thank you.

They are very flat ( wider of course ). In a 1U rack one can fit a 100VA O-core.
I only see advantages over classic toroidals. In theory, O-core is optimum, efficiency, iron and copper losses, flux leakage.
Do you see drawbacks ?
Do you recommend a manufacturer.
I am looking for low powers: Less than 40VA

Good morning folks,

I am resuming my cd player retromod project after some time away from it. Being snowed in doesn't leave you with much to do. I have hit kind of a dead end though. I need a datasheet for the Sony CXD1135Q. It would be bundled with the 1125Q and 1130Q. The datasheet I have been able to find online is only 6 pages, and I am needing the section that talks about how it operates (commands, timing), not just pinouts. My search keeps leading back to some posts on the diyAudio forum that mention a more complete version available, around 37 pages or more for these DSPs. The last page of the 6 page version indicates at least 260 pages. Really, I am just looking for the detailed info on the 1135Q, its commands and timing stuff. The links posted on this forum that lead to vasiltek.nm.ru aren't working for me.

I would greatly appreciate some help tracking this down. Stay warm folks!

Hi I have a KAC PS401m on the bench stuck in protection mode flashing also low battery led on.

The crossover board had the usual corrosion from sticky fibre tape, I've removed the tape, cleaned up the corroded traces and pads, re run the solder and tested the traces for continuity also replaced the capacitors on the board and its made no difference, the relays don't click on and the aforementioned remained flashing/on.

Any ideas on what to check next would be appreciated.

Hi

Long story short, amp turns on but produces gibberish at it's output. No shorted, burnt, damaged stuff.

Quick check did not find any missing or out of tolerance auxiliary or main supply voltages. All seems fine. No heating.

I've checked the class D switching frequency , one of the drivers (IR2010) is switching at 120khz but the other one at 330khz. Shouldn't they produce the same ? Shape is also a bit odd for the 120khz.
The inputs to the drivers (HIN and LIN) are inline with the output(LO and HO), so 120khz comes in 120khz comes out, so I suppose it's not the ICs...it is doing what it's being told to do so.

I do have a service manual but it's for the bigger brother from the same series Alpine MRD-M1005, so i've used that as a reference. I'm trying to understand what is setting the switching frequency input to the driver and why it is so much different.

It’s common to find any installations placed the electronic (or active) crossover after preamplifier (and before power amplifier), in both home and car audio. While the equalizer is usually found to be placed in “tape monitor” loop or before the preamplifier.

What’s the reason for those installations? What will happen if the EQ is placed after preamplifier and the crossover is placed before the preamplifier?

Hey there I'm pretty new to all of this but recently got into more audio-related things. I would like to build my own speakers in the future, working with wood and researching how to make them sound better, maybe soldering things as well.

Hi, i am building a 350w +/-60v isolated SMPS. I recently finished a succesfull DC-DC converter, so this is my first time using a gate drive transformer to isolate the switching circuitry from the half bridge.
My first prototype (input rectifier and output caps + inductor on seperate board, no heatsinks yet):


The unregulated smps i have built is working pretty nice so far however i would love any improvements and suggestions with the circuit, but also i am a little stuck on what to do with the "proportional drive winding", that i will explain.


Highlighted in red from pins 5-2 of the GDT, is what i will call the "proportional winding" though this is probably the wrong terminology. Follow it along and you see that this winding going through the gdt actually links the main transformer(U1) to the half bridge! The reason for this winding through the GDT is to help the SMPS startup, by providing a little bump on one of the GDT gate drive secondaries, which is enough to start up the auxilary winding on U1 for the tl494, which quickly takes control over GDT.
I belive the "proportional winding" is also to help supply a bit of extra current to the GDT's secondaries to provide a little extra gate drive current.
The problem is, im not sure how many windings i should do for the proportional winding. Unfortuanately, this GDT transformer i bought has no data sheet, so i am unaware of how many windings there are for its gate drive secondaries. I had to hand wind the proportional winding onto the GDT, and at the moment i am using 3 turns. I could vary the number of proportional winding turns and take osc measurements, but i dont know what GDT output i should be aiming for.

GDT secondary drive winding oscilloscope measuement without any current flowing through the proportional winding (TL494 externally suplied):

GDT secondary drive winding osc measurement with the SMPS fully on, current flowing through U1 and proportional winding:

Drive circuitry on primary side of GDT, if of any help: