Have fun with your weird nerdish stuff!
Until you posted in this thread yesterday you haven' posted in this forum since 2012, and this is how you choose to do it?
You are really a class act, dude!
I've done some modeling of the FIR group-delay-correction filter using the technique described earlier in this thread. The results are encouraging.
Here is an overview of what I have done.
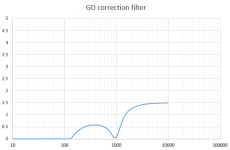
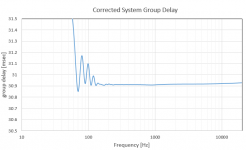
1. I start with the desired group delay EQ curve. This was shown earlier in this post or see first attachment.
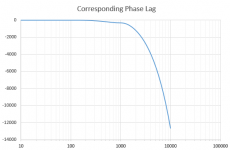
2. I calculate the corresponding phase lag by integrating, using the definition of group delay. The result is attachment 2. Note the phase is shown unwrapped. This data is still on the equally-logarithmic-spaced frequency grid from another program.
3. In the next step, I interpolate the phase onto the equal-linear-spacing frequency grid that will be used for the discrete transform processing.
4. I then generate the real and imaginary components of the complex number that results for this phase angle, with the magnitude of the response equal to 1.0. These are pretty boring so I don't bother to show them here. I make sure that H(k) = H*(N-k).
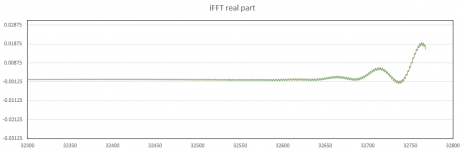
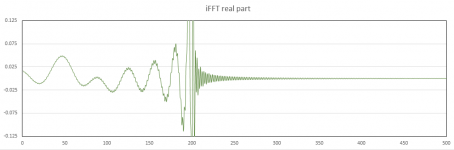
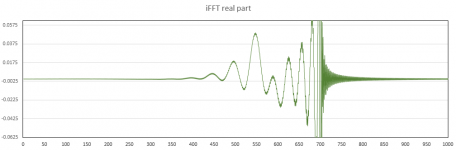
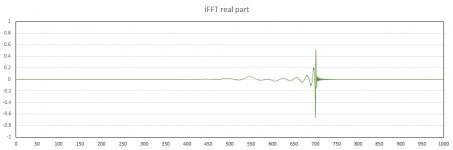
5. I take the inverse DFT of the real and imaginary components to transform the response to the time domain. The output has both a real and an imaginary component, however, the imaginary component is essentially zero. To show what is going on I have attached plots of the "beginning" of the real data as well as the "end" (with additional magnification). These correspond to time near zero for positive time values and negative time values.
6. I manipulate the real component of the time domain response (the impulse). The data is shifted "to the right" to move the part of the impulse that is at small negative times (at the "end") to positive time. I then apply a rectangular window to the data, setting everything outside the window to zero. The imaginary component of the time domain response is also set to zero. The remaining non-zero values are the FIR filter coefficients.
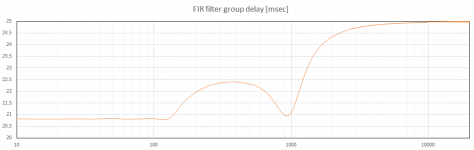
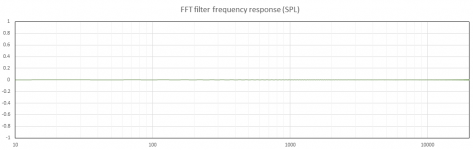
7. What will the response of this FIR filter look like? To find out, I perform the forward DFT on the shifted, windowed impulse to bring the data back into the frequency domain. I then calculate and plot the filter SPL, the phase, and finally the group delay. This is shown as the last two attached plots.
The FIR filter magnitude (SPL) is very flat across the 20-20k frequency band, with deviations of much less than 0.1dB. The group delay plot shows that the filter produces the desired group delay EQ, plus latency (frequency independent delay) of about 20.75 milliseconds.
QED.
.
Here is an overview of what I have done.
1. I start with the desired group delay EQ curve. This was shown earlier in this post or see first attachment.
2. I calculate the corresponding phase lag by integrating, using the definition of group delay. The result is attachment 2. Note the phase is shown unwrapped. This data is still on the equally-logarithmic-spaced frequency grid from another program.
3. In the next step, I interpolate the phase onto the equal-linear-spacing frequency grid that will be used for the discrete transform processing.
4. I then generate the real and imaginary components of the complex number that results for this phase angle, with the magnitude of the response equal to 1.0. These are pretty boring so I don't bother to show them here. I make sure that H(k) = H*(N-k).
5. I take the inverse DFT of the real and imaginary components to transform the response to the time domain. The output has both a real and an imaginary component, however, the imaginary component is essentially zero. To show what is going on I have attached plots of the "beginning" of the real data as well as the "end" (with additional magnification). These correspond to time near zero for positive time values and negative time values.
6. I manipulate the real component of the time domain response (the impulse). The data is shifted "to the right" to move the part of the impulse that is at small negative times (at the "end") to positive time. I then apply a rectangular window to the data, setting everything outside the window to zero. The imaginary component of the time domain response is also set to zero. The remaining non-zero values are the FIR filter coefficients.
7. What will the response of this FIR filter look like? To find out, I perform the forward DFT on the shifted, windowed impulse to bring the data back into the frequency domain. I then calculate and plot the filter SPL, the phase, and finally the group delay. This is shown as the last two attached plots.
The FIR filter magnitude (SPL) is very flat across the 20-20k frequency band, with deviations of much less than 0.1dB. The group delay plot shows that the filter produces the desired group delay EQ, plus latency (frequency independent delay) of about 20.75 milliseconds.
QED.
.
Attachments
In the post above, the inverse FFT used 32768 points to generate the impulse response, however, after the windowing was applied only 2000 points had non-zero values. This produced a smooth and error free result. Let's see what happens as we reduce the number of coefficients further.
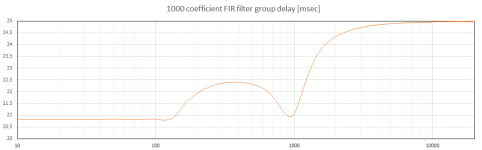
When we window out all but 1000 points from the impulse response (e.g. use 1000 FIR filter taps) some small artifacts start to appear. The first two attachments show the FIR filter SPL and group delay. Some small oscillations are starting to appear in the filter SPL. These are still extremely small, much less than 0.1dB, and are negligible. Small deviations also begin to appear in the group delay, for instance around 100Hz the delay dips slightly before rising and above and below 100Hz there some oscillations are visible. Note that the latency has been reduced.
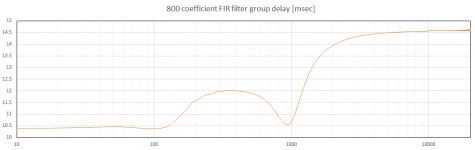
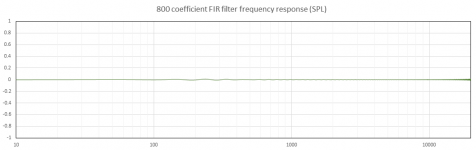
The next two plots show the result for 800 points. The oscillations have slightly increased but are still not very significant. Again, the latency has been further reduced.
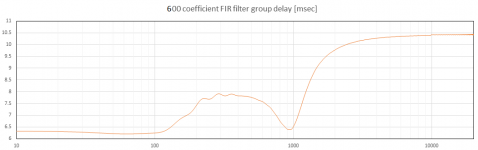
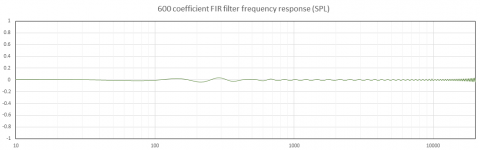
The next two plots show the result for 600 points. The deviations increase further, while latency is reduced as well.
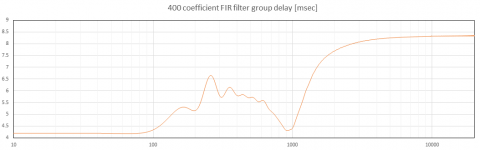
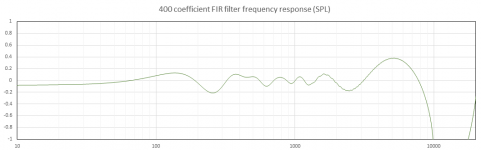
The last two plots show the response for 400 points. At this point we are starting to truncate enough of the impulse that it is having more significant effects. The frequency response now has a large deviation above 10kHz that is off scale in the plot (it reaches -1.5dB before coming back up). The group delay response is starting to show some more significant deviations and oscillations.
It seems that in this case an FIR filter with well under 1000 taps (as low as 600) would be sufficient for correcting the group delay but not changing the frequency response. Another type of window function may allow even fewer points to be used. It's surprising that even with only a few hundred taps, the group delay correction is largely implemented correctly. It remains to double check the time domain response of the truncated FIR filters so see what artifacts, if any, are present there.
When we window out all but 1000 points from the impulse response (e.g. use 1000 FIR filter taps) some small artifacts start to appear. The first two attachments show the FIR filter SPL and group delay. Some small oscillations are starting to appear in the filter SPL. These are still extremely small, much less than 0.1dB, and are negligible. Small deviations also begin to appear in the group delay, for instance around 100Hz the delay dips slightly before rising and above and below 100Hz there some oscillations are visible. Note that the latency has been reduced.
The next two plots show the result for 800 points. The oscillations have slightly increased but are still not very significant. Again, the latency has been further reduced.
The next two plots show the result for 600 points. The deviations increase further, while latency is reduced as well.
The last two plots show the response for 400 points. At this point we are starting to truncate enough of the impulse that it is having more significant effects. The frequency response now has a large deviation above 10kHz that is off scale in the plot (it reaches -1.5dB before coming back up). The group delay response is starting to show some more significant deviations and oscillations.
It seems that in this case an FIR filter with well under 1000 taps (as low as 600) would be sufficient for correcting the group delay but not changing the frequency response. Another type of window function may allow even fewer points to be used. It's surprising that even with only a few hundred taps, the group delay correction is largely implemented correctly. It remains to double check the time domain response of the truncated FIR filters so see what artifacts, if any, are present there.
Attachments
-
 400_coefficient_FIR_group_delay.PNG27.6 KB · Views: 92
400_coefficient_FIR_group_delay.PNG27.6 KB · Views: 92 -
 400_coefficient_FIR_frequency_response.PNG28.1 KB · Views: 88
400_coefficient_FIR_frequency_response.PNG28.1 KB · Views: 88 -
 600_coefficient_FIR_group_delay.PNG19.1 KB · Views: 94
600_coefficient_FIR_group_delay.PNG19.1 KB · Views: 94 -
 600_coefficient_FIR_frequency_response.PNG25.3 KB · Views: 95
600_coefficient_FIR_frequency_response.PNG25.3 KB · Views: 95 -
 800_coefficient_FIR_group_delay.PNG27.4 KB · Views: 86
800_coefficient_FIR_group_delay.PNG27.4 KB · Views: 86 -
 800_coefficient_FIR_frequency_response.PNG24.1 KB · Views: 93
800_coefficient_FIR_frequency_response.PNG24.1 KB · Views: 93 -
 1000_coefficient_FIR_group_delay.PNG27.6 KB · Views: 80
1000_coefficient_FIR_group_delay.PNG27.6 KB · Views: 80 -
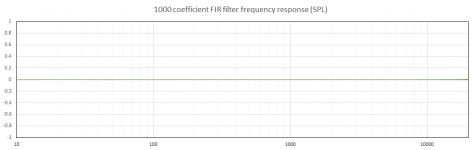 1000_coefficient_FIR_frequency_response.PNG23.3 KB · Views: 105
1000_coefficient_FIR_frequency_response.PNG23.3 KB · Views: 105
I've been getting some more experience with the process of generating the FIR filter to EQ delay (e.g. linearize the phase). I discovered it is important to "tailor" the phase so that the real and imaginary components undergo a seamless transition at the half-sampling-rate boundary. Doing this minimizes the noise in the impulse and eliminates some of the ripples and deviations in the resulting filter delay, especially at high frequencies, that can arise after windowing the impulse. You can see an example of this kind of high frequency noise in the zoomed view of the impulse response in the last post.
I have also experimented with a correction filter that provides linear-phase/flat-delay to a lower frequency: 50Hz. Because the filter has non-zero phase changes at lower frequencies than the previous examples, the window width must be increased proportionally. The first attachment shows the filter with 5000 taps in orange with the target delay curve in green. Filter latency is 46 milliseconds because of the window width used. When the width is reduced to 2500 taps some small oscillations in the delay start to appear but the latency is almost halved. Further reduction in the number of taps causes the amplitude of these oscillations to become excessive, however, 2500 taps is still a very economical filter size for creating a linear phase system response to 50Hz. This makes the application of FIR "lightweight" and processing can be done with very little latency.
One other trick that I have implemented can be seen in the plots. Previously the target delay EQ curve had an abrupt transition upwards from zero at low frequency. For the correction down to 50Hz, the slope of this was steeper and the transition more discontinuous. This caused some ringing in the filter response because a very large number of taps is needed to reproduce sharp features. To alleviate the discontinuity, I introduced a smooth transition in place of the discontinuity. This helps the filter have smoother response overall for a given number of taps, and/or allows fewer taps to be used for the same general level of reproduction of the target EQ curve.
By implementing a couple of tricks I have been able to create very lightweight (e.g. a low number of taps) FIR filters that can change the loudspeaker response so that it has linear phase above a user-determined frequency. This is something that I plan to include in future loudspeaker crossover projects.
.
I have also experimented with a correction filter that provides linear-phase/flat-delay to a lower frequency: 50Hz. Because the filter has non-zero phase changes at lower frequencies than the previous examples, the window width must be increased proportionally. The first attachment shows the filter with 5000 taps in orange with the target delay curve in green. Filter latency is 46 milliseconds because of the window width used. When the width is reduced to 2500 taps some small oscillations in the delay start to appear but the latency is almost halved. Further reduction in the number of taps causes the amplitude of these oscillations to become excessive, however, 2500 taps is still a very economical filter size for creating a linear phase system response to 50Hz. This makes the application of FIR "lightweight" and processing can be done with very little latency.
One other trick that I have implemented can be seen in the plots. Previously the target delay EQ curve had an abrupt transition upwards from zero at low frequency. For the correction down to 50Hz, the slope of this was steeper and the transition more discontinuous. This caused some ringing in the filter response because a very large number of taps is needed to reproduce sharp features. To alleviate the discontinuity, I introduced a smooth transition in place of the discontinuity. This helps the filter have smoother response overall for a given number of taps, and/or allows fewer taps to be used for the same general level of reproduction of the target EQ curve.
By implementing a couple of tricks I have been able to create very lightweight (e.g. a low number of taps) FIR filters that can change the loudspeaker response so that it has linear phase above a user-determined frequency. This is something that I plan to include in future loudspeaker crossover projects.
.
Attachments
Last edited:
I'm not sure what you are seeing for plots in post #26. To me it appears that you've got 300 samples of low frequency ringing before apparent peak at about sample 700, and after wards high frequency ringing that trails beyond plot.
Not sure what your worries about latency are. 46ms or 23ms, in either case this is useless for live applications, or use with video without using video delay.
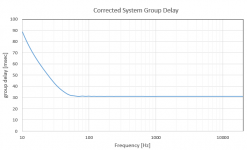
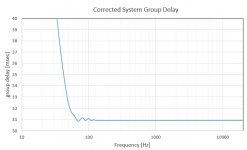
This is typical group delay results I get with FIR:
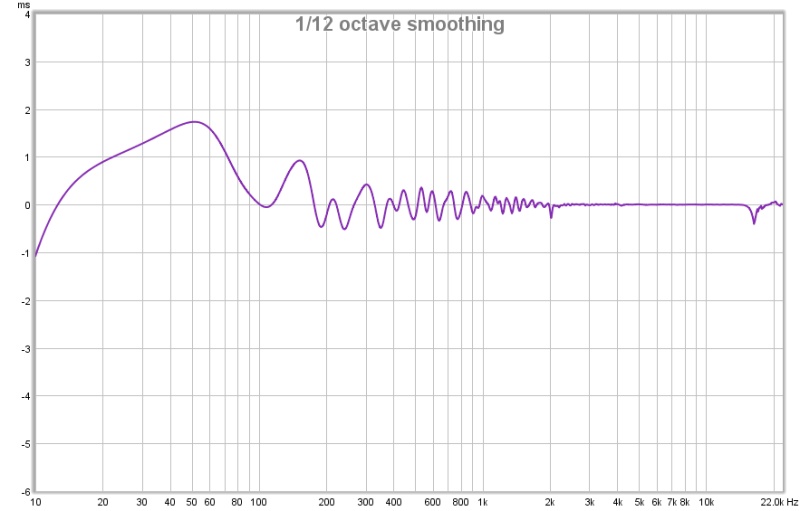
Not sure what your worries about latency are. 46ms or 23ms, in either case this is useless for live applications, or use with video without using video delay.
This is typical group delay results I get with FIR:

Sure, that's nice, but how many taps are required (or are you just using some "black box" correction system)? With my filter correction, the group delay would look the same (except possibly smoother) above 50Hz, and rising below that frequency, while using very few taps. Maybe I did not make that clear enough...
Honestly I could really care less about live applications. I listen to music and I don't watch any "video". But if I did I could just delay the video stream. Something that's s pretty standard, as you seem to know.
As for the impulse response in post #26, this is the impulse of the FIR FILTER when different frequencies are delayed by different amounts that are essentially the REVERSE of the usual delay for those frequencies. Instead of more delay for low frequencies and less to zero delay for high frequencies the impulse shown has more delay for high frequencies and less delay for low frequencies. This is why the "spike" part of the impulse comes "later" - it's delayed WRT the other frequencies. Maybe you were thinking it was the impulse of the system AND filter?
Honestly I could really care less about live applications. I listen to music and I don't watch any "video". But if I did I could just delay the video stream. Something that's s pretty standard, as you seem to know.
As for the impulse response in post #26, this is the impulse of the FIR FILTER when different frequencies are delayed by different amounts that are essentially the REVERSE of the usual delay for those frequencies. Instead of more delay for low frequencies and less to zero delay for high frequencies the impulse shown has more delay for high frequencies and less delay for low frequencies. This is why the "spike" part of the impulse comes "later" - it's delayed WRT the other frequencies. Maybe you were thinking it was the impulse of the system AND filter?
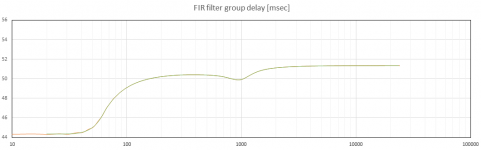
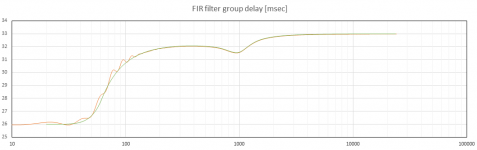
To make it more clear, I have attached the group delay for the system+FIR filter delay EQ. In this case the group delay was equalized down to about 60Hz (AKA linear phase). I also did two level of zoom, to make low level details more clear. Please note that these are just the modeled system+filter. I have not yet actually implemented the FIR filter on a real system. This is just my attempt at filter design for a special application, using as few taps as possible.
The filter should be able to make the group delay flat above whatever frequency the user desires. Reducing the lowest frequency of delay correction requires that the number of taps are increased dramatically and I want to use as small of a number of taps as possible. As a result I only EQ the delay above some low frequency where the ear is not very sensitive to delay (e.g. 100Hz or so). If the number of taps was not of concern the delay correction can be applied as low in frequency as desired.
The filter should be able to make the group delay flat above whatever frequency the user desires. Reducing the lowest frequency of delay correction requires that the number of taps are increased dramatically and I want to use as small of a number of taps as possible. As a result I only EQ the delay above some low frequency where the ear is not very sensitive to delay (e.g. 100Hz or so). If the number of taps was not of concern the delay correction can be applied as low in frequency as desired.
Attachments
Many thanks for creating this thread.
Very interesting!
Now 2 years later, perhaps you can update it with listening impressions.

I don't listen to group delay. I listen to loudspeakers. Each one is different and sounds different. Group delay equalization is just another part of the crossover system. Unless your GD is really high to begin with, the difference is honestly very, very minor. I currently just implement a good IIR design without any GD flattening and leave it at that.
I am afraid that you expected to hear that "veils were lifted with amazingly improved PRAT" or some similar gibberish...
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.
- Home
- Source & Line
- PC Based
- group delay equalization