Friend has a pair of old Cerwin Vega PD-3 PA speakers which need midranges-not just diaphragms, there is a hole where the midranges used to be.
Found out the midrange on this model is the Cerwin Vega H25.
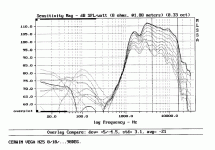
Looking at the frequency response, which I found here, I noticed that this unit seems to be putting out 112 dB @ 1M/1Watt.
Chart is reproduced below.
Win ISD will not allow simulations above 106 dB at 1M/1 Watt.
Small's chart for bass response tops out at 112 dB at 1M/1 Watt.
Seems to me this chart shows the Cerwin Vega, through part of it's band, as being either 100% efficient or 400% efficient, 6 dB meaning 4 times the power. Even 100% efficiency seems far fetched, 50% efficiency is superb.
Any help understanding this would be appreciated.
Found out the midrange on this model is the Cerwin Vega H25.
Looking at the frequency response, which I found here, I noticed that this unit seems to be putting out 112 dB @ 1M/1Watt.
Chart is reproduced below.
Win ISD will not allow simulations above 106 dB at 1M/1 Watt.
Small's chart for bass response tops out at 112 dB at 1M/1 Watt.
Seems to me this chart shows the Cerwin Vega, through part of it's band, as being either 100% efficient or 400% efficient, 6 dB meaning 4 times the power. Even 100% efficiency seems far fetched, 50% efficiency is superb.
Any help understanding this would be appreciated.
Attachments
KW,
According to this calculator 112dB at 1 watt translates to an efficiency rating of 1 or 100%
http://www.sengpielaudio.com/calculator-efficiency.htm
According to this calculator 112dB at 1 watt translates to an efficiency rating of 1 or 100%
http://www.sengpielaudio.com/calculator-efficiency.htm
This is dependent upon the radiation pattern of the device. Remember, when you measure 112 dB you are measuring the intensity (power per unit area) at that point, not the power being radiated by the device. The reference intensity I_o is 10^-12 watts/m^2, and SPL is given by
SPL = 10*log(I/I_o) = 120 + 10*log(I)
so if you have 1 watt of full space radiation you get
SPL = 120 + 10*log( 1w / 4pi ) = 109
or in half space you get
SPL = 120 + 10*log( 1w / 2pi ) = 112
If, for a rough approximation, you treat the device as if it has uniform axisymmetric radiation with an exact beamwidth of x degrees, then the area radiated over at 1 m is 2*pi*(1 - cos(x/2)) so the SPL for 1 watt of radiation is:
SPL = 120 + 10*log(1 / 2*pi*(1 - cos(x/2)) ) = 120 - 10log(2pi) - 10*log(1 - cos(x/2)) = 112 - 10*log(1 - cos(x/2))
A couple sample values:
BW SPL
360 109
180 112
120 115
90 117.3
60 120.7
I hope this helps
Nolen
SPL = 10*log(I/I_o) = 120 + 10*log(I)
so if you have 1 watt of full space radiation you get
SPL = 120 + 10*log( 1w / 4pi ) = 109
or in half space you get
SPL = 120 + 10*log( 1w / 2pi ) = 112
If, for a rough approximation, you treat the device as if it has uniform axisymmetric radiation with an exact beamwidth of x degrees, then the area radiated over at 1 m is 2*pi*(1 - cos(x/2)) so the SPL for 1 watt of radiation is:
SPL = 120 + 10*log(1 / 2*pi*(1 - cos(x/2)) ) = 120 - 10log(2pi) - 10*log(1 - cos(x/2)) = 112 - 10*log(1 - cos(x/2))
A couple sample values:
BW SPL
360 109
180 112
120 115
90 117.3
60 120.7
I hope this helps
Nolen
Rybaudio- I started to do the same calc, but got lost right at the beginning. How do you get from the 0dB level of 0.0002 dynes/cm^2 to watts/cm^2? There's something really simple I'm missing!
Conrad Hoffman said:
I guess that Rybaudio was using approxmate value of 10^-12 W/m2 right away as it is commonly used in calculations like this.
I found following http://en.wikipedia.org/wiki/Sound_power
P=(A*p^2)/Z
Z is the acoustic impedance of air, at +25c about 410 (Pa*s/m)
SPL 0db reference level of 20uPascal translates then to 20u*20u*1m2/410 =0.976pW/m2 which rounds up to easy 10^-12 W/m2
I got that value from a reference textbook a while back and have used it so many times that I just remember it. I think it was in Kinsler and Frey's Fundamentals of Acoustics, but I'm not sure and right now most of my books are packed away in a move.
If the loudspeaker has 100% efficiency and if it is fed with 1W of electrical power, the acoustical power will also be 1W. This power is distributed over a sphere, in this case we look at a radius of 1 m.
If the loudspeaker is omnidirectional and radiates in full space, the power will be evenly distributed over the surface of 4 pi m², and the intensity will be 1/(4*pi) W/m². This corresponds to a sound intensity level of 10*log(1/(4*pi*10^-12))= 109 dB.
If the loudspeaker instead radiates in half space, power is distributed over the surface of the half sphere, which is 2 pi m², and the sound intensity level becomes 10*log(1/(2*pi*10^-12))= 112 dB.
Other directional patterns can give higher levels, in theory infinitely high (well...).
If the loudspeaker is omnidirectional and radiates in full space, the power will be evenly distributed over the surface of 4 pi m², and the intensity will be 1/(4*pi) W/m². This corresponds to a sound intensity level of 10*log(1/(4*pi*10^-12))= 109 dB.
If the loudspeaker instead radiates in half space, power is distributed over the surface of the half sphere, which is 2 pi m², and the sound intensity level becomes 10*log(1/(2*pi*10^-12))= 112 dB.
Other directional patterns can give higher levels, in theory infinitely high (well...).
Hi,
I just read the last post,
No point in reading the rest, I know we can rely on the accuracy of Svante's posts.
Nice understandable explantion, I now know where this 4Pi etc comes from.
I just read the last post,
No point in reading the rest, I know we can rely on the accuracy of Svante's posts.
Nice understandable explantion, I now know where this 4Pi etc comes from.
kelticwizard said:
Hi,
Svante's post explains 112db/W/1m, what about 106dB/W/1m ?
IMO this is due to the fact maximum efficiency of a speaker by definition is
when the air loads match and this give a maximum acoustic efficiency of 50%.
Which = 106dB/W/1m into half space = Win ISD.
🙂/sreten.
Thanks for the conversion info- now things make a bit more sense. I was always led to believe that driver efficiency was dismal, like a couple percent at best. Now it seems that things aren't quite that bad.
Re: Re: Which dB @1M/1Watt Constitutes 100% Efficiency?
Hmm... Interesting thought. But I wonder, is this really the maximum efficiency that is possible? Or does it, theoretically speaking, correspond to the acoustic load that would maximize the acoustic output of a given driver?
These are slightly different.
sreten said:
Hmm... Interesting thought. But I wonder, is this really the maximum efficiency that is possible? Or does it, theoretically speaking, correspond to the acoustic load that would maximize the acoustic output of a given driver?
These are slightly different.
Hi,
If the acoustic load is increased any further then bandwidth may become very restricted.
But mount it in a properly designed horn and the numbers go the other way.
I suspect that when the acoutic load presented by the horn is good enough to match the driver + cable resistance then the bandwidth will be restricted.
If the acoustic load is increased any further then bandwidth may become very restricted.
yes, the driver on it's own is dismal. When mounted in a conventional box it drops even further to a few tenths of a percent.
But mount it in a properly designed horn and the numbers go the other way.
AndrewT said:
Ah, well , my line of reasoning is completely away from normal loudspeakers and horns. I mean, horns can at best reach 50% efficiency, but I was wondering if a higher efficiency at all is possible. Like, if we change the medium from air to water or if we go to ultrasonics or something like that.
My sensation is that if we get the acoustic impedance to dominate completely, 100% efficiency is the theoretical maximum.
...even though this is very, very far from possible in practice with normal speakers or even horns. And bandwidth is not a concern at all in this.
Hmmm........
Wouldn't a theoretically perfect massless diaphragm constant charge (how does that work with a massless
diaphragm) push-pull electrostatic with super conductive transformers with super magnetic cores hit 100% ?
That is act as a perfect capacitor except for the losses, which are all acoustic ?
🙂/sreten.
Wouldn't a theoretically perfect massless diaphragm constant charge (how does that work with a massless
diaphragm) push-pull electrostatic with super conductive transformers with super magnetic cores hit 100% ?
That is act as a perfect capacitor except for the losses, which are all acoustic ?
🙂/sreten.
- Status
- Not open for further replies.