Everything I read about poles and zeros seems to be somewhat complex and mathematical and related to feedback loops. But I've seen the terms being used in filter design. As far as I know, a pole is the single stage of a filter (6db/oct).
So when does the transition from pole to zero and zero to pole occur?
So when does the transition from pole to zero and zero to pole occur?
Poles and zeros come from the fact that the frequency response of an analogue circuit is a rational function of frequency. A zero is a frequency where the numerator (or one of the numerator expressions) is zero - this may be a complex frequency. A pole is where a denominator term is zero. I don't know what you mean by a transition from pole to zero.
To put it simple:
for a transfer function f (x)= A/B where A and B can be any real or complex function from x of any order, zeros are when A=0 and Poles when B=0.
In filters it’s A that makes the transfer of the filter goes down and B that makes the filter goes up.
A Riaa filter for instance has 2 zeros at 3180 usec and 75 usec and one pole at 318 usec.
Poles and zeros have nothing to do with feedback loops.
Hans
for a transfer function f (x)= A/B where A and B can be any real or complex function from x of any order, zeros are when A=0 and Poles when B=0.
In filters it’s A that makes the transfer of the filter goes down and B that makes the filter goes up.
A Riaa filter for instance has 2 zeros at 3180 usec and 75 usec and one pole at 318 usec.
Poles and zeros have nothing to do with feedback loops.
Hans
The way I understand it, somewhat simplified, is that a zero is a term in the numerator of the transfer function, and a pole is a term in the denominator.
If a first-order term in the numerator becomes zero you get a 6dB/oct 1st order roll off.
If a first-order term in the denominator becomes zero, the response turns up at 6dB/oct.
So an R-C in the forward path is a 1st order term in the numerator and rolls off the response. Placing this R-C in the feedback path, or placing a C-R in the forward path, turns the response up
I think. 😱
BTW It is probably much more effective to look it up at Google rather than relying on incomplete and possibly confusing or contradictory reply avalanche here 😉
Edit: I see others beat me to it while I was typing...
Jan
If a first-order term in the numerator becomes zero you get a 6dB/oct 1st order roll off.
If a first-order term in the denominator becomes zero, the response turns up at 6dB/oct.
So an R-C in the forward path is a 1st order term in the numerator and rolls off the response. Placing this R-C in the feedback path, or placing a C-R in the forward path, turns the response up
I think. 😱
BTW It is probably much more effective to look it up at Google rather than relying on incomplete and possibly confusing or contradictory reply avalanche here 😉
Edit: I see others beat me to it while I was typing...
Jan
Last edited:
The loop gain of a feedback loop has poles and zeros, because it too is a rational function of frequency. Where they are tells you about loop stability.Hans Polak said:
No idea what games of logic have to do with the false statement "Poles and zeros have nothing to do with feedback loops." Did you mean to say 'feedback loops have nothing to do with poles and zeros'?
A resistor R with V=I * R has nothing particlular to do with feedback loops.
But in modelling feedback loops resistors play an important role.
Poles and Zeros with f(x) = A/B have in particular nothing to do with feedback loops.
But in modelling feedback loops poles and zeros play an important role.
There you have your oaks and trees.
But in modelling feedback loops resistors play an important role.
Poles and Zeros with f(x) = A/B have in particular nothing to do with feedback loops.
But in modelling feedback loops poles and zeros play an important role.
There you have your oaks and trees.
If someone could get yet an other stab at explaining this I would appreciate it. Please an other angle on the analogy?
//
//
What is unclear in the first few posts with explanations, which all say basically the same?
Clearing that up might be better than coming up with yet another similar explanation?
Jan
Clearing that up might be better than coming up with yet another similar explanation?
Jan
Last edited:
Write down the formula for the frequency response of an RC first order low pass filter. If necessary, simplify it so that it ends up in the form 1/A, where A is a first order function of frequency. What value of frequency makes A=0? That is the pole.
If you can do this then you can begin to understand poles. If you cannot do this then you cannot understand poles, however much we explain them.
If you can do this then you can begin to understand poles. If you cannot do this then you cannot understand poles, however much we explain them.
I understand a pole as the point where the level is changing from being linear to an up or downwards slope due to an effect from a reactive (C or L) component. What I don't get is the 0.
//
//
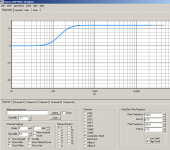
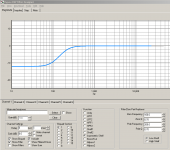
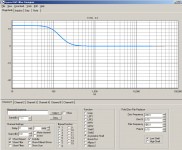
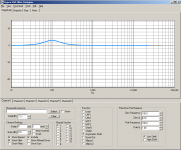
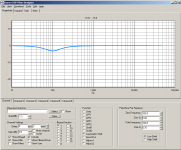
The Hypex filter designer has a "Asymmetric Shelf" with zero and pole parameters.
Check the high/low shelf setting down/right and "Pole/Zero pair replacer"...
//
Check the high/low shelf setting down/right and "Pole/Zero pair replacer"...
//
Attachments
Last edited:
If you put in a pole, the response bends upward, right? Then you put in a zero a bit further in freq, where it bends down so it becomes flat again. That's the shelf in your screen shot.
Jan
Jan
Think about a CR first order high pass filter and the corresponding RC low pass filter. They have a pole at exactly the same place. The difference is that the high pass also has a zero at the origin. The high pass response rises from zero frequency until it meets the pole, where it levels off. You could think of this as being the combination of an ever rising response and a low pass - beyond the corner frequency they cancel each other.
- Status
- Not open for further replies.