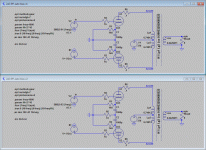
Hi all,
I've recently developed more interest in PP amps, and been researching different output stage configurations. While looking at the plain old auto-biased topology I came across an interesting (to me - at least) twist. Have a look at the attached two variants.
Top is the plain bypassed auto bias config, while at the bottom I added a shared resistor ("R5") connecting the bypass caps to ground. If chosen appropriately, I found this resistor may reduce H3 (and other odd harmonics) by several dB. In this case from ~1% to below .1%.
I found this to work with several different triodes and 43% UL connected pentodes, but not pure pentodes or even 20% UL.
Can anyone explain more profoundly what's going on here?
Cheers,
GB
I've recently developed more interest in PP amps, and been researching different output stage configurations. While looking at the plain old auto-biased topology I came across an interesting (to me - at least) twist. Have a look at the attached two variants.
Top is the plain bypassed auto bias config, while at the bottom I added a shared resistor ("R5") connecting the bypass caps to ground. If chosen appropriately, I found this resistor may reduce H3 (and other odd harmonics) by several dB. In this case from ~1% to below .1%.
I found this to work with several different triodes and 43% UL connected pentodes, but not pure pentodes or even 20% UL.
Can anyone explain more profoundly what's going on here?
Cheers,
GB
Attachments
Hi, odd harmonics level can be reduced by NFB. As you added a resistor to 1000u, it increased the degeneration which is similar to increase of NFB level. The time constant of 1000u and 51 is 0.05 which is about 20Hz, the bottom gain is reduced so degeneration is increased and odd harmonic level reduced. You should check H3 at different reference input freq and see what happened do you still see the same result?
Frequency does have an influence, but very little when I simulate a "perfect" OPT. Also, the size of the caps is not too important. The dominant influence comes thru the resistor.
Maybe I need to look up some texts on degeneration - I'm no EE by trade - but it's certainly not nfb which is acting here. The gain of the circuit is virtually unaffected.
Maybe I need to look up some texts on degeneration - I'm no EE by trade - but it's certainly not nfb which is acting here. The gain of the circuit is virtually unaffected.
There is a paper about this effect:
"System Design Factors for Audio Amplifiers" by M.V. Kiebert and P.R. Mallory Co.
bottom of page 2
http://www.clarisonus.com/Archives/...System Design Factors for Audio Ampifiers.pdf
It lowers other odd harmonics too, but takes a somewhat different tail R for nulling different harmonics. Set it for what sounds best. You may want to null 5th or 7th as first priority.
One is essentially getting the near square power law (I = k Vg^2) of grid 1 lowered (by degeneration) to near the 1.5 power law of grid 2 for better constant Mu tracking. (Grid 1 suffers grid wire proximity effects next to the cathode, raising its textbook 1.5 power law to nearer 2.0. It changes with current though, dropping at higher current, causing Mu curves to flatten out by themselves at some high plate current.)
The Western Electric "Harmonic Neutralizer" works similarly, but is described (in its patent) in terms of re-entrant frequency mixer effects.
"System Design Factors for Audio Amplifiers" by M.V. Kiebert and P.R. Mallory Co.
bottom of page 2
http://www.clarisonus.com/Archives/...System Design Factors for Audio Ampifiers.pdf
It lowers other odd harmonics too, but takes a somewhat different tail R for nulling different harmonics. Set it for what sounds best. You may want to null 5th or 7th as first priority.
One is essentially getting the near square power law (I = k Vg^2) of grid 1 lowered (by degeneration) to near the 1.5 power law of grid 2 for better constant Mu tracking. (Grid 1 suffers grid wire proximity effects next to the cathode, raising its textbook 1.5 power law to nearer 2.0. It changes with current though, dropping at higher current, causing Mu curves to flatten out by themselves at some high plate current.)
The Western Electric "Harmonic Neutralizer" works similarly, but is described (in its patent) in terms of re-entrant frequency mixer effects.
Last edited:
Woops, "grid 2" in the above post should be "plate" for triodes.
This scheme --could-- work for pentodes if the load R did not overwhelm the tube output Rp and ruin the 200X Mu gain feedback (a tiny amount). High % UL configurations could get the Rp and Mu lowered enough to work like the triode case.
This scheme --could-- work for pentodes if the load R did not overwhelm the tube output Rp and ruin the 200X Mu gain feedback (a tiny amount). High % UL configurations could get the Rp and Mu lowered enough to work like the triode case.
Last edited:
Essentially what is happening is that the added resistor allows the second harmonic current (always present in a PP stage, but cancelling in the OPT) to develop some second harmonic voltage at the cathodes. This then mixes with the incoming signal via the second-order distortion of the valves to create some 3rd. If this 3rd happens to be of the opposite sign to the 3rd already generate by the valves then you get some cancellation. It is an example of re-entrant distortion.
Thanks DF96,
this also explains why it works best with triodes and to a lesser degree with 43% UL pentodes, where H2 > H3. With pure pentodes (or 20% UL) it does not work, because H3 > H2.
this also explains why it works best with triodes and to a lesser degree with 43% UL pentodes, where H2 > H3. With pure pentodes (or 20% UL) it does not work, because H3 > H2.
No. For virtually all active devices at virtually all signal levels 2nd order distortion is greater than 3rd order. The issue is whether the intrinsic 3rd has the right sign for the re-entrant 3rd to cancel it or increase it.
If it's about distortion intrinsic to the device, how come the scheme works with 43% UL connected EL84, but not with 20% taps or even pentode connected? You mean the amount of local feedback flips the sign of the 3rd harmonic intrinsic to the device itself??
It is easier to see in the time domain.
Take a look at pages 5,7, and 9 of the E55L datasheet:
http://frank.pocnet.net/sheets/009/e/E55L.pdf
On page 5 is the gm (S) curve for pentode versus Vg1. Where it linearly ramps in the center region, the tube V to I power law is 2.0 or I = k Vg^2. Gm being the 1st derivative of that, comes out linear: gm = 2kVg
Where the gm curve bends upward on the left (--Vg or low current) the V to I power law is higher than 2.0. Where the gm curve bends downward or over on the right (higher current) the V to I power law is less than 2.0.
Two pentodes in P-P can be put together in class A complementary overlap such that the linear gm ramp portions (even the outer curved regions approximately) sum to a constant gm, giving linear gain. This can also be looked at as an LTP with a 0 Ohm tail corrector. (ie, maximum 3rd harmonic correction from maximum tail current variation)
Now look at page 9. Gm versus plate plate current for fixed Va (and Vg2 in triode). A square law V to I gives gm = 2 k k SQRT(I/k). Summing two of these curves in P-P class A will give a big gm hump in the center. So a CCS tail for pentodes is no good for linearity.
But for triodes with the CCS tail, when you consider the plate feedback and a constant Mu with hi Z loads, they will operate at a single current over the CCS tail. So constant gm sum occurs at the single operating point.
For a real triode pair with real loading, the current changes along the humped gm sum curve. By putting some tail resistance in, the triodes can be altered to draw more current toward the signal peaks (the tail voltage rises at extremes). More current means more gm. So the tail R can be adjusted to flatten the gm hump.
The additional imperfection of g1 operating in a range around 2.0 power law and g2 operating near 1.5 power law causes additional Mu variation with current, which means the current must vary some to maintain a constant Mu. A similar fix for this with the tail R.
The triodes act as very low power law devices due to the plate feedbacks, so they have a very slightly humped gm curve versus plate current, which is fixable with a modest (high R) tail mod.
However, the tail R fix requires slightly different R values to null different odd distortion harmonics. It may be possible to null a whole range of odd harmonics by using a thermionic diode tail in place of the R tail, with an adjustable CCS pull-up on the tail to activate the correct curvature of the diode corrector.
Pentodes at 2.0 power law are at the maximum fixable limit (by tail R = 0).
Above 2.0 power law (pentodes at low current) would require a negative R tail. (gm sum sagging in the center needs an opposite fix) This might be possible by swapping the positions of the thermionic diode and adjustable CCS mentioned above.
Putting some UL feedback on the pentode screens will also lower the power law (getting closer to the practical triode case by lowering the Mu and Rp from the pentode case) (the pentode case actually already is a triode, just very high Mu and Rp. The Rp feedback effect just gets wiped out by loads that are too low)
Take a look at pages 5,7, and 9 of the E55L datasheet:
http://frank.pocnet.net/sheets/009/e/E55L.pdf
On page 5 is the gm (S) curve for pentode versus Vg1. Where it linearly ramps in the center region, the tube V to I power law is 2.0 or I = k Vg^2. Gm being the 1st derivative of that, comes out linear: gm = 2kVg
Where the gm curve bends upward on the left (--Vg or low current) the V to I power law is higher than 2.0. Where the gm curve bends downward or over on the right (higher current) the V to I power law is less than 2.0.
Two pentodes in P-P can be put together in class A complementary overlap such that the linear gm ramp portions (even the outer curved regions approximately) sum to a constant gm, giving linear gain. This can also be looked at as an LTP with a 0 Ohm tail corrector. (ie, maximum 3rd harmonic correction from maximum tail current variation)
Now look at page 9. Gm versus plate plate current for fixed Va (and Vg2 in triode). A square law V to I gives gm = 2 k k SQRT(I/k). Summing two of these curves in P-P class A will give a big gm hump in the center. So a CCS tail for pentodes is no good for linearity.
But for triodes with the CCS tail, when you consider the plate feedback and a constant Mu with hi Z loads, they will operate at a single current over the CCS tail. So constant gm sum occurs at the single operating point.
For a real triode pair with real loading, the current changes along the humped gm sum curve. By putting some tail resistance in, the triodes can be altered to draw more current toward the signal peaks (the tail voltage rises at extremes). More current means more gm. So the tail R can be adjusted to flatten the gm hump.
The additional imperfection of g1 operating in a range around 2.0 power law and g2 operating near 1.5 power law causes additional Mu variation with current, which means the current must vary some to maintain a constant Mu. A similar fix for this with the tail R.
The triodes act as very low power law devices due to the plate feedbacks, so they have a very slightly humped gm curve versus plate current, which is fixable with a modest (high R) tail mod.
However, the tail R fix requires slightly different R values to null different odd distortion harmonics. It may be possible to null a whole range of odd harmonics by using a thermionic diode tail in place of the R tail, with an adjustable CCS pull-up on the tail to activate the correct curvature of the diode corrector.
Pentodes at 2.0 power law are at the maximum fixable limit (by tail R = 0).
Above 2.0 power law (pentodes at low current) would require a negative R tail. (gm sum sagging in the center needs an opposite fix) This might be possible by swapping the positions of the thermionic diode and adjustable CCS mentioned above.
Putting some UL feedback on the pentode screens will also lower the power law (getting closer to the practical triode case by lowering the Mu and Rp from the pentode case) (the pentode case actually already is a triode, just very high Mu and Rp. The Rp feedback effect just gets wiped out by loads that are too low)
Last edited:
- Status
- Not open for further replies.
- Home
- Amplifiers
- Tubes / Valves
- Please explain this H3 3rd harmonic cancellation