Hi I've searched everywhere? but cant seem to find any math formulas for making a shelving filter for my Audio Nirvana 10 inchers (or any other speaker for that matter).
I'd prefer formula's as opposed to giving particular numbers and getting the answer.
Scottmoose alluded to this in post #26 of the Fostex 206E Horn failure this last March.
Thanks again for all your help.
Hopefully I'll post pics of my finished open baffle speakers soon!
Paul
I'd prefer formula's as opposed to giving particular numbers and getting the answer.
Scottmoose alluded to this in post #26 of the Fostex 206E Horn failure this last March.
Thanks again for all your help.
Hopefully I'll post pics of my finished open baffle speakers soon!
Paul
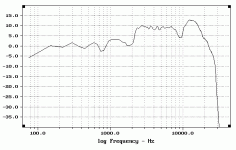
For starters, here's a 1M on axis curve in a large flat open baffle.
It's probable that you will not want to EQ this to flat, but rather to
about half way, and you will likely want to vary the shelving frequency
and amplitude to taste.
I'll think about an example for you, unless someone else would like
to jump in.
😎
It's probable that you will not want to EQ this to flat, but rather to
about half way, and you will likely want to vary the shelving frequency
and amplitude to taste.
I'll think about an example for you, unless someone else would like
to jump in.
😎
Attachments
Hi
NP has it right, that is the circuit, but i can add a little more detail.
Search "baffle step loss" for more explaining.
Depends on the baffle dimension, width in particular.
see http://www.tolvan.com/edge/help.htm
In the program see circuit 1, where R1 represents the speaker impedance, mostly Re between f1-f2.
Nominally R2 = R1 for 6 dB of baffle step which is IMO quite large, ie assumes no reinforcement from room boundaries. So adjust R2 for taste try 4-5 dB to start.
PS If you build it (baffle step compensation) at line level, it has several advantages over using large power inductors and resistors.
NP has it right, that is the circuit, but i can add a little more detail.
Search "baffle step loss" for more explaining.
Depends on the baffle dimension, width in particular.
see http://www.tolvan.com/edge/help.htm
In the program see circuit 1, where R1 represents the speaker impedance, mostly Re between f1-f2.
Nominally R2 = R1 for 6 dB of baffle step which is IMO quite large, ie assumes no reinforcement from room boundaries. So adjust R2 for taste try 4-5 dB to start.
PS If you build it (baffle step compensation) at line level, it has several advantages over using large power inductors and resistors.
Thanks for the help.
So a BSC is going to act like a shelving filter. No effect below a certain freq. gradually increasing in impedance to higher freq. and then levelling off at a certain freq. where the decrease in freq. stays constant?
Any mathematical formula?
I'd like to be able to plug in #'s and see the change with different values.
Thanks,
Paul
So a BSC is going to act like a shelving filter. No effect below a certain freq. gradually increasing in impedance to higher freq. and then levelling off at a certain freq. where the decrease in freq. stays constant?
Any mathematical formula?
I'd like to be able to plug in #'s and see the change with different values.
Thanks,
Paul
I pulled that up with MicroCap 9. You can download a student edition
from spectrum software. If you want to do that, I'll email you the
file.
www.spectrum-soft.com/demo.shtm
😎
from spectrum software. If you want to do that, I'll email you the
file.
www.spectrum-soft.com/demo.shtm
😎
Thanks for all your help everyone.
I think for ease and quickness, I'll give Nelsons idea a try first.
If it works out, I'll have quite a smooth response from 100 Hz- 8kHz, then a reticent treble by about 4 dB above that.
I think I found the formula's I was interested in.
Inductive Reactance = 2pi(F)(L)
Capacitive Reactance = 1/2pi(F)(C)
Then when you have a cap, coil, and resistor in parallel with each other, in series with the driver (shelving network) you use
1/R(total)= 1/R1 + 1/R2 + 1/R3
and you can figure the new resistance in series with the driver at various frequencies and see the new response.(?)
If Rtotal = ? do I expect to see a drop in dB of ?
Have I left anything out , or am I on the wrong track.
I just want to know how it actually works.
Paul
I think for ease and quickness, I'll give Nelsons idea a try first.
If it works out, I'll have quite a smooth response from 100 Hz- 8kHz, then a reticent treble by about 4 dB above that.
I think I found the formula's I was interested in.
Inductive Reactance = 2pi(F)(L)
Capacitive Reactance = 1/2pi(F)(C)
Then when you have a cap, coil, and resistor in parallel with each other, in series with the driver (shelving network) you use
1/R(total)= 1/R1 + 1/R2 + 1/R3
and you can figure the new resistance in series with the driver at various frequencies and see the new response.(?)
If Rtotal = ? do I expect to see a drop in dB of ?
Have I left anything out , or am I on the wrong track.
I just want to know how it actually works.
Paul
- Status
- Not open for further replies.
- Home
- Loudspeakers
- Full Range
- how to make a shelving filter? for FR