Zero padding an FFT does not increase frequency resolution (no information has been added) but the visual appearance of the plot of the bins becomes easier to discern. It is a band limited interpolation process, the interpolated plot has a higher resolution view of the original data but it has not increased the resolution of that data, both the unpadded and padded views have the same information content. Here is a helpful post with some pictures to clarify: Zero Padding in FFT - Signal Processing Stack Exchange and NI have an old paper that may help: Zero Padding Does Not Buy Spectral Resolution - National Instruments
I am posting an answer here to some question from over at "Uniform directivity" because this discussion does not belong there.
First thing that readers need to understand is that the time/frequency tradeoff, sometimes called the Heisenberg Uncertainty Principle (HUP) is NOT a characteristic of nature, but of the Fourier Transform. In quantum mechanics there is a fundamental connection between a wave function in time and space and this connection is the Fourier integral/transform. Hence, for particles the HUP is fundamental in nature. But it is not so for sampled signals. They do not have to obey the Fourier limitations unless Fourier transforms are actually used. There are many other ways. None of them are as fast (or as simple) as the FFT and that is why it reigns in "typical" applications. But in virtually all advanced applications it is never used for all the reasons that we see here.
The FFT is what is called a Non-parametric Spectral Estimator - non-parametric since its frequencies are fixed by the algorithm and all that is found are the values (complex) at those frequencies. There is a whole world of other techniques called Parametric Spectral Estimators which are entirely different that the FFT in every respect, the most important being they do not have a HUP or any form of limitations based on data length or widows etc. These techniques dominate in geological sounding and most importantly (and best known to me) underwater sonar. In those highly advanced areas the FFT is simply never used because it is a very poor technique.
Parametric techniques fall into a class of study called "Statistical Signal Processing", on which there are dozens and dozens of text books. In this area of study one must abandon concepts like HUP, and low frequency limits, windows, and any form of "certainty" because everything becomes "estimates" and "uncertainty" - data points become Degrees-of-freedom, etc. But please understand that these "estimates" are virtually always better than anything the FFT can produce (the two techniques converge for large data sets and low SNR). So while they are called 'estimates" they are often the best estimates that can be obtained.
One can "estimate" a signals frequency, strength and decay based on data that only lasts a very short time, certainly well before the signal has completely decayed. This means that the HUP does not apply. Recently there has been a rash of discussion of how our hearing violates the HUP. To many this may seem surprising but to me it was "natural" - there is no low frequency limit to what our brains can "guess" at. And it turns out that we become pretty good at these guesses - far exceeding the HUP limit of the FFT.
So this whole idea that the "resolution" of a measurement is fundamentally limited by the "window" of data is absurd - it doesn't exist. It's there only because people are thinking of FFTs and not the signals themselves.
If I wanted to I could write an algorithm that would yield an "estimate" of the frequency response for any given window length all the way to DC. The algorithm would also tell me how "certain" I could be at every frequency in that "estimate". Some frequencies would be better than others and some, like DC, would be pretty bad if the data length was small. But by increasing the data length I could increase my "confidence" up to the point where the noise in the signal was reached. This is exactly the same limit as the FFT, but for short signals the "confidence" in the result is far better for the Parametric approach than the non-Para approach.
Why do I use the FFT?, because for what we do it works fine. There is no need to go to the more elaborate techniques because windowing and zero padding is all well understood and works just fine. See Liberty Software (Laud, I believe) if you want to see what can be done with these other techniques. There simply is no need to worry about using windowed FFT data as only an incompetent user would get fooled by its errors.
In my polar map program I do use some parametric techniques for the angular data, but not for the frequency data - because there is no need to!! I would if this were an advantage - its not.
First thing that readers need to understand is that the time/frequency tradeoff, sometimes called the Heisenberg Uncertainty Principle (HUP) is NOT a characteristic of nature, but of the Fourier Transform. In quantum mechanics there is a fundamental connection between a wave function in time and space and this connection is the Fourier integral/transform. Hence, for particles the HUP is fundamental in nature. But it is not so for sampled signals. They do not have to obey the Fourier limitations unless Fourier transforms are actually used. There are many other ways. None of them are as fast (or as simple) as the FFT and that is why it reigns in "typical" applications. But in virtually all advanced applications it is never used for all the reasons that we see here.
The FFT is what is called a Non-parametric Spectral Estimator - non-parametric since its frequencies are fixed by the algorithm and all that is found are the values (complex) at those frequencies. There is a whole world of other techniques called Parametric Spectral Estimators which are entirely different that the FFT in every respect, the most important being they do not have a HUP or any form of limitations based on data length or widows etc. These techniques dominate in geological sounding and most importantly (and best known to me) underwater sonar. In those highly advanced areas the FFT is simply never used because it is a very poor technique.
Parametric techniques fall into a class of study called "Statistical Signal Processing", on which there are dozens and dozens of text books. In this area of study one must abandon concepts like HUP, and low frequency limits, windows, and any form of "certainty" because everything becomes "estimates" and "uncertainty" - data points become Degrees-of-freedom, etc. But please understand that these "estimates" are virtually always better than anything the FFT can produce (the two techniques converge for large data sets and low SNR). So while they are called 'estimates" they are often the best estimates that can be obtained.
One can "estimate" a signals frequency, strength and decay based on data that only lasts a very short time, certainly well before the signal has completely decayed. This means that the HUP does not apply. Recently there has been a rash of discussion of how our hearing violates the HUP. To many this may seem surprising but to me it was "natural" - there is no low frequency limit to what our brains can "guess" at. And it turns out that we become pretty good at these guesses - far exceeding the HUP limit of the FFT.
So this whole idea that the "resolution" of a measurement is fundamentally limited by the "window" of data is absurd - it doesn't exist. It's there only because people are thinking of FFTs and not the signals themselves.
If I wanted to I could write an algorithm that would yield an "estimate" of the frequency response for any given window length all the way to DC. The algorithm would also tell me how "certain" I could be at every frequency in that "estimate". Some frequencies would be better than others and some, like DC, would be pretty bad if the data length was small. But by increasing the data length I could increase my "confidence" up to the point where the noise in the signal was reached. This is exactly the same limit as the FFT, but for short signals the "confidence" in the result is far better for the Parametric approach than the non-Para approach.
Why do I use the FFT?, because for what we do it works fine. There is no need to go to the more elaborate techniques because windowing and zero padding is all well understood and works just fine. See Liberty Software (Laud, I believe) if you want to see what can be done with these other techniques. There simply is no need to worry about using windowed FFT data as only an incompetent user would get fooled by its errors.
In my polar map program I do use some parametric techniques for the angular data, but not for the frequency data - because there is no need to!! I would if this were an advantage - its not.
First of all we are talking here specifically about impulse response and NOT anything that those papers are referring to. The impulse response is unique because you are guaranteed that it goes to zero. And adding zeros IS adding information - precisely the information that I just mentioned - we know that the signal has to go to zero - that's "new information" to the algorithm! the only question is "How fast". But that's entirely different than saying that we are not adding any new information - we are.
Zero padding does not work for signals that do not decay monotonically - that is well know. But impulses responses are in a class of their own and techniques that do not work elsewhere do work here.
No. If you have an input data sequence to FFT (that's what we are talking about here) in the form {a1, a2, ... aN, 0, 0, 0, ... ,0 } where aN is the last nonzero element, then the result will be just a "smoother" look at the data obtained from the sequence {a1, a2, ..., aN } alone, regardless the actual data - be it impulse response or whatever. This is simple math. The same resolution, no more information.
The rest of your post is undoubtely very interesting (I'd loved to read more), but nothing at all what was discused here so far.
Yes, and you're using it here, claiming you have a 5Hz resolution data from 5ms time window above 200Hz. That's just not possible with FFT, unless you count all the interpolated values comming from zero-padding.
Last edited:
Again, you're making an assumption about "how fast". Measuring isn't about making assumptions, it's about showing "how fast".
Correct but nobody disagreed so far. It really doesn't matter if you add that "new" information if the IR goes to zero anyway. The question really is "how do you know the IR goes to zero without actually measuring it"?
Because, as I said, it has to, that's guaranteed, and it has to monotonically, which means that once it falls below say .01 of the max it can't ever grow above that point. This is fundamental to the whole discussion.
But as a side note- I stopped using an FFT and I now use an Nth order Prony series (where N is 48000 Hz x .006 sec = 288 Degrees of freedom) which gives me infinite resolution from DC to Nyquist. No window problems, no low frequency limit - Nada. Discussion of resolution of windows is now moot.
I'll have to respectfully disagree with you on that. If an impulse response really were zero outside some bounded time (i.e. it had compact support) it would have a Fourier transform of infinite extent (or to be more mathematically precise, the FT would be an entire function) - just as a dirac does. There is always some truncation going on when a measured impulse response is windowed and that inevitably takes a toll. It is easy enough to show the effect by creating an artificial IR, I produced one for a speaker with a perfectly flat response between 20Hz and 10 kHz (-3 dB) and one for the same speaker with a 6 dB, Q=10 dip at 1 kHz. I then applied a 5 ms Tukey 0.25 window post peak and plotted a 256k FFT for each (48k sample rate, so lots and lots of zero padding). Here are the results. The 6 dB dip is now a 5 dB dip with a ripple. No amount of zero padding is going to recover the original responses above 200 Hz, the only way to reduce the ripple in the windowed responses would be to use a much smoother window taper, but that would correspondingly reduce the resolution with which the dip is resolved and make it look even shallower.
Despite their ripple, the plots look enormously better than they would if I had used an FFT that only spanned the 5ms window duration, of course, and the centre frequency of the dip is accurately identified. Perhaps that is all you are claiming? Any one of a number of parametric methods would do a better job of recovering the original signal of course, in this case with only 6 poles in the response and noise at the numerical precision of the signal a dozen points would likely do the job (but not zero ones
).
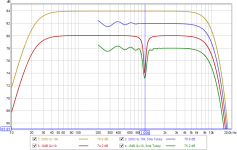
I'll have to respectfully disagree with you on that. If an impulse response really were zero outside some bounded time (i.e. it had compact support) it would have a Fourier transform of infinite extent (or to be more mathematically precise, the FT would be an entire function) - just as a dirac does. There is always some truncation going on when a measured impulse response is windowed and that inevitably takes a toll. It is easy enough to show the effect by creating an artificial IR, I produced one for a speaker with a perfectly flat response between 20Hz and 10 kHz (-3 dB) and one for the same speaker with a 6 dB, Q=10 dip at 1 kHz. I then applied a 5 ms Tukey 0.25 window post peak and plotted a 256k FFT for each (48k sample rate, so lots and lots of zero padding). Here are the results. The 6 dB dip is now a 5 dB dip with a ripple. No amount of zero padding is going to recover the original responses above 200 Hz, the only way to reduce the ripple in the windowed responses would be to use a much smoother window taper, but that would correspondingly reduce the resolution with which the dip is resolved and make it look even shallower.
Despite their ripple, the plots look enormously better than they would if I had used an FFT that only spanned the 5ms window duration, of course, and the centre frequency of the dip is accurately identified. Perhaps that is all you are claiming? Any one of a number of parametric methods would do a better job of recovering the original signal of course, in this case with only 6 poles in the response and noise at the numerical precision of the signal a dozen points would likely do the job (but not zero ones
View attachment 372820
Thanks for posting what you discovered. I think that your argument would have much more weight if you also posted the impulse response for the signal with the dip. Can you post that?
The impulse duration in the time domain of a spectral feature is really what is determining how long of a window must be used. For instance in post #2 of this thread, I showed the case of a narrow Q=20, +6dB peak at 2.1kHz that could be resolved quite well with a 5ms window, even though that is only supposed to "see" things with a 200Hz resolution. But the peak's shape and center frequency (2,100 Hz or 10.5 times the resolution) are very well represented in the frequency domain resulting from the 5ms long window. This was using a 50% Hahn window, which as you say should be worse at resolving these features.
I did some more testing yesterday and today with peaky responses. If I put a peak with about a 200Hz wide bandwidth at a lower frequency (+6dB, Q=5, 300Hz), it couldn't be seen at all (more or less) with a 5ms window, while the peak at 2.1kHz that I mentioned above looks very nice, even when part of the impulse from it is truncated. All I can say is that the impulse from the 300Hz peak is ringing longer because it is at a lower frequency. If you eliminate too much of the time domain response of a particular feature, it just will not appear in the frequency response. Period. At this point I am not so sure that you can make the assumption that "a 5ms window means you can't see anything narrower than 200Hz anywhere" since this just doesn't seem to be quite true. But I think it is fair to say if your impulse has not died out then you will be eliminating something, and that could just be the low frequency part of the response or it could be a mid-frequency peak or dip, it just depends on how that feature come out in the time domain and where your window ends.
By the way on page 3 of the Sterophile article "Time Dilation" the author mentions that KEF developed a method by which they attenuated the low frequency response to "help" the impulse die down enough before the end of the window, then applied the inverse filter to the resulting frequency response. I thought that was interesting so I tried it in a few variations to get a feel for what that does. Essentially it doesn't help anything, e.g. it didn't improve the recovery of any peaks that I put in around 200-300 Hz (using the 5ms gate). After the whole process was done, there were still errors in the frequency response. These stemmed mostly from the fact that, as was mentioned earlier in one of these threads (by Earl I think) that the frequency response eventually has an "upturn" due to a DC offset in the impulse response resulting from the truncation (if I got what he was saying). This "upturn" caused the frequency response to start deviating "upwards" in SPL from what I knew was the correct FR. I could replace the upturn with a 12dB/oct tail, but at what frequency to do this seemed to be guesswork, although after doing so I could get the SPL accuracy to be within about 2-3dB down to 20Hz, like they claim. But the response was just a smooth one - you could just generate it using a box model and splice it together with the gated FR in the frequency domain and get about the same thing, so this technique doesn't seem to really offer any new potential in my eyes.
Yes, of course, there is always some error from using any finite signal, no matter how long (< infinity), that's a rather obscure point and was NOT the question here. The point is that this error IS NOT a broadband limit to the resolution of that of the data window before padding, because that is wrong. The resolution is that of the padded data set - albeit with errors that can be made insignificant.
As Charlie asked does the impulse in your example decay visibly to zero? Or is the truncation obvious? We all agree that using a too short window is a problem (garbage in garbage out), what we do not agree on is if using a window can ever be done with insignificant errors and "smoothing" or not. No one is arguing that this can't be done wrong, we are arguing if it can be done right.
A 'good" speaker has an impulse response that is quite compact and insignificant errors result from using a window that is tapered only towards the end (not sure if this is what Tukey .25 meant or not - few would use a full width tapered window.)
I think that time locking in Holm is a completely different animal - absolutely essential, but not related.
I don't see at all how that thread has much of anything to do with the topic we are discussing here...
Again Charlie you are right on the money - this is exactly correct. It is not that a window is error free, its just that it is not resolution limiting across the bandwidth and it is not a problem that a savvy experimenter cannot resolve. That's why I say that posting the un-windowed impulse response should clear up all concerns. I plan to start doing that so that people can see that I am not chopping off significant data.
Well, actually that is what I did... I reported the bandwidth incorrectly in post #2. It should be:
BW=Q/Fo
and we have Fo=2100 and Q=20 so the bandwidth of that feature was actually 100 Hz.
It's a 100 Hz BW peak resolved (the degree to which can be debated) with a 5ms / 200 Hz window. Some posters seem to think that resolving this peak at all is impossible by virtue of a property of the FFT and the result shown in the plot below from post #2 is evidence to the contrary:
It all comes down to what the data captured in your impulse window can tell you.
Post #23I don't see at all how that thread has much of anything to do with the topic we are discussing here...
No, definitely not!
It's a little complicated for an "EQ" peak. EQ is obtained by summing a bandpass filtered version of a signal with the original signal. For high Q peaks, the definition of "Q" for the bandpass filter is very close to what you get for the EQ peak, however, as you noted the peak has "tails" and when the Q is low the definition of bandwidth used for a bandpass filter doesn't describe the width of an EQ peak accurately. The "width" of the bandpass filter is measured at 0.707 of its maximum, e.g. only partway down, and the bandpass function keeps spreading out before it "blends into the original signal", thus at "the base of the peak" the signal+EQ is wider than the EQ bandwidth.
This figure illustrates what I said above:
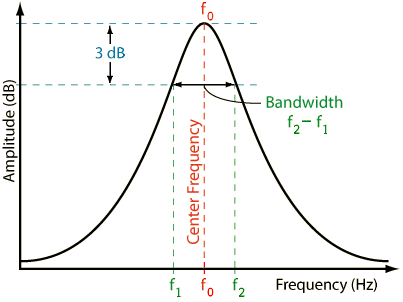
Last edited:
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.