Thanks... I looked that up also 🙂
So, what I'm trying to get at is if the entire peak is within 100 Hz, how does the response look? Maybe such a high Q peak does not exist. But at least it will disprove (or prove 😱) the notion that a 5ms gate has magically achieved more resolution than is allowed by the FFT.
So, what I'm trying to get at is if the entire peak is within 100 Hz, how does the response look? Maybe such a high Q peak does not exist. But at least it will disprove (or prove 😱) the notion that a 5ms gate has magically achieved more resolution than is allowed by the FFT.
Nobody says that it magically achieves "more resolution" it is just not as simple as saying that the resolution is that of the window and that "200 Hz smoothing" occurs across the band.
Please, lets keep the argument straight, its complicated enough as it is.
Please, lets keep the argument straight, its complicated enough as it is.
and on and on
"Show how it is possible to determine the height of a tall building with the aid of a barometer."
"Take a barometer to the top of the building, attach a long rope to it, lower the barometer to the street and then bring it up, measuring the length of the rope. The length of the rope is the height of the building."
etc. etc.
Go at it guys. Great entropy generator. 🙂
"Show how it is possible to determine the height of a tall building with the aid of a barometer."
"Take a barometer to the top of the building, attach a long rope to it, lower the barometer to the street and then bring it up, measuring the length of the rope. The length of the rope is the height of the building."
etc. etc.
Here you go:Thanks for posting what you discovered. I think that your argument would have much more weight if you also posted the impulse response for the signal with the dip. Can you post that?
You can see two distinct elements in the decay of the IR. The very slow decays are those of the 20 Hz high pass, the faster oscillation superimposed on top is from the dip. I also had a look at a response with a 200 Hz high pass, effect on the 1k dip was the same though of course the HP decay part happened correspondingly faster. I've attached a wav file of the IR in case you wanted to play with it, format is mono, 32-bit signed PCM, normalised.
View attachment 20hz to 10k with 6dB dip.zip
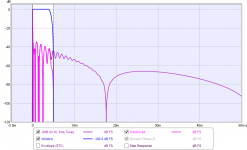
I'll have to respectfully disagree with you on that. If an impulse response really were zero outside some bounded time (i.e. it had compact support) it would have a Fourier transform of infinite extent (or to be more mathematically precise, the FT would be an entire function) - just as a dirac does. There is always some truncation going on when a measured impulse response is windowed and that inevitably takes a toll. It is easy enough to show the effect by creating an artificial IR, I produced one for a speaker with a perfectly flat response between 20Hz and 10 kHz (-3 dB) and one for the same speaker with a 6 dB, Q=10 dip at 1 kHz. I then applied a 5 ms Tukey 0.25 window post peak and plotted a 256k FFT for each (48k sample rate, so lots and lots of zero padding). Here are the results. The 6 dB dip is now a 5 dB dip with a ripple. No amount of zero padding is going to recover the original responses above 200 Hz, the only way to reduce the ripple in the windowed responses would be to use a much smoother window taper, but that would correspondingly reduce the resolution with which the dip is resolved and make it look even shallower.
Despite their ripple, the plots look enormously better than they would if I had used an FFT that only spanned the 5ms window duration, of course, and the centre frequency of the dip is accurately identified. Perhaps that is all you are claiming? Any one of a number of parametric methods would do a better job of recovering the original signal of course, in this case with only 6 poles in the response and noise at the numerical precision of the signal a dozen points would likely do the job (but not zero ones 🙂).
View attachment 372820
Now that you have also posted the impulse I think I have a better idea of what you did in your experiment.
Here is a repost of the frequency response from your original post:

Here are my thoughts:
1. The ripple is just a consequence of using the Tukey window and not a consequence of the dip (I think you inferred that). I'm not so sure that a narrower window will eliminate the dip. Did you try other windows?
2. The partial resolution of the dip is a result of the window width used. You used a dip having Fo=1000Hz and Q=10. The bandwidth of that peak is: BW=Fo/Q = 100Hz. The 5ms window that you used is only supposed to resolve features that are 1/5ms=200Hz or larger. It's no wonder that the dip is "partially" resolved, e.g. you get a slightly wider dip that is only 5dB deep. Also, the plot of your impulse and windowing clearly show that you are excluding part of the ringing resulting from the dip, which would likely remove some of the info about it. All in all it seems that the peak is recovered better than it is "supposed to", and there is more "detail" in the shape of the peak than if you just connected points spaced 200Hz apart, which is what (I feel) others have suggested in this thread and the "Uniform Directionality" thread that spawned this one.
It took me a little while to figure out what I was looking at in your impulse. I have never seen a plot of one that uses a log y-axis (e.g. SPL). Since the impulse will oscillate about zero and can do that even at short times, there will be those nulls like what is seen at about 17ms. Was this intentional? I'm curious about it. Also, what software is that? REW?
I used a log axis as it makes it easier to see the truncations that occur when an impulse response is windowed. There are two factors at play here, the effects of truncation and the effects of FFT length, it is worth dealing with each separately.It took me a little while to figure out what I was looking at in your impulse. I have never seen a plot of one that uses a log y-axis (e.g. SPL). Since the impulse will oscillate about zero and can do that even at short times, there will be those nulls like what is seen at about 17ms. Was this intentional? I'm curious about it.
Truncating an impulse will produce ripples in the frequency response and will alter the response somewhat depending on what has been removed. The ripples can be reduced by using windows which taper more smoothly, but correspondingly more of the original signal is modified by such a window so the frequency response is more significantly altered. What the frequency response plots show is the response of a system which has an impulse the same as the one that was obtained after the window was applied - since that response has been forced to die away more quickly, it of necessity has a shallower and slightly broader dip at 1 kHz, since that is the kind of dip that would give the windowed response.
To explain the effects of FFT length, it may be helpful to recap a little on what an FFT is, and more generally on how signals can be represented to aid with their mathematical manipulation. Signals can be described in terms of the weights (or strengths) of a set of basis functions - the basis functions are the ingredients, and the weights tell us how much of each to include. For a time signal expressed as a series of samples at regular time intervals, the most common basis functions are vectors that have a 1 at a single sample position and zero at all the others, so the first basis function would be [1, 0, 0, 0, ....], the second would be [0, 1, 0, 0, 0, 0, ...] etc. If our time signal consisted of the sample sequence 0.25, 0.39, 0.42, ... then we could express that as 0.25 times the first basis function plus 0.39 times the second plus 0.42 times the third etc. That may seem very contrived, but for various kinds of signal manipulation such contrivances are very useful.
A Fourier Transform uses a different set of basis functions, sine waves, at frequencies with periods which are integer multiples of the transform length. So if the transform length was 5 ms, for example, the frequencies would 0 Hz, 200 Hz, 400 Hz etc. If the transform length was 1000 ms the frequencies would be 0 Hz, 1 Hz, 2 Hz, etc. The amplitudes and phases of each of those sinusoids are the basis function weights. When we plot a frequency response produced by taking the FFT of an impulse response, what we are really plotting is the weights of those individual basis functions.
There are some important characteristics to bear in mind here: firstly, the transform preserves all the information of the original signal, nothing is lost and nothing is added. It is simply a different way of representing the same original collection of sample values. Secondly, the transform values are only valid at the specific frequencies of the transform, so if the transform is 5 ms long it gives amplitude and phase values for 0, 200, 400, 600 Hz etc. It does not tell you anything about any intermediate frequencies, since they have not been used to make this representation of the signal. When the transform is plotted (our frequency response) the individual points are usually joined up, with either straight lines or some other interpolation method, but that is strictly for the visual convenience of those viewing the plot, the fact that there is a line between the amplitude at 200 Hz and the amplitude at 400 Hz does not let you infer anything about what amplitude the frequency response should have at 300 Hz, to know that you would have to use a longer transform (e.g. 10 ms) so that the basis functions become 0, 100 Hz, 200 Hz, 300 Hz, ... and you would then have a 300 Hz value to play with.
For a short signal, like the 5 ms windowed impulse response, a mathematician would usually use the shortest possible transform, since that would be the most compact representation and retains all the information content of the original time series. If we are primarily interested in knowing information about the levels of specific frequencies in that time signal, however, we would typically use a much longer transform to provide the detail we seek.
So, with the theory out of the way, what does that mean practically. Windowing (truncating) the impulse response alters the sample values and discards those outside the window. The windowed signal will have a different frequency response than the unwindowed one, depending on how much information we have discarded - if the original signal had sharp changes in its frequency response, those would have corresponding slowly decaying features in the impulse which will have been modified by the windowing, resulting in them being less sharp in the frequency response of the windowed signal (windowing the time response corresponds to a form of low pass filtering of the frequency response). We can still locate those frequencies with high precision, however, by using a long transform (zero padding), we just won't be able to see how sharp they originally were.
If the original response had lots of sharp features, the effect of windowing may blur them to the extent that those individual features become smeared together and can no longer be distinguished. So how close do they need to be before they merge into one? That depends somewhat on the relative sizes of the features, but for features of similar sizes blurring occurs at separations below the lower frequency bound of the window width, i.e. 200 Hz for a 5 ms window. Here are some plots for two 6 dB Q=10 dips separated by 100 Hz, 150 Hz and 200 Hz. The first dip is at 1.025 kHz in each case.
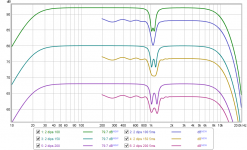
Looking in more detail at the case with 200 Hz separation, the second filter is at 1.225 kHz and the bottom of the dip in the unwindowed response is at 1.223 kHz due to the effect of the nearby filter. In the 5 ms windowed response the minimum occurs at 1.231 kHz, so the centre frequency of the dip has been resolved well, just 8 Hz from the unwindowed value.
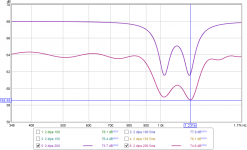
Overall then, applying windows typically adds some ripple to the response; it has a low pass filtering effect, which will blur sharp transitions; feature separated by less than the lower bound may no longer be distinguishable, but the frequencies of isolated features and those separated by more than the lower bound can still be resolved with good frequency accuracy.
I think that means everyone was right 😉
Last edited:
Thanks, JohnPM.
I'd like to point out one important thing that maybe wasn't stressed enough -
If this wasn't the case, it would be possible to get even more "true" data simply by shortening the window - use one sample less then before and instead of [200, 400, 600Hz,...] you would have data for something like e.g. [201, 402, 603Hz,...] and so on. Repeating this and merging the results one could "fill" much of the missing data from 200Hz up. This is not the case, however, and won't work this way.
I'd like to point out one important thing that maybe wasn't stressed enough -
- This does not mean that at these frequencies the values are "true". It's already smeared/averaged here.Secondly, the transform values are only valid at the specific frequencies of the transform, so if the transform is 5 ms long it gives amplitude and phase values for 0, 200, 400, 600 Hz etc.
If this wasn't the case, it would be possible to get even more "true" data simply by shortening the window - use one sample less then before and instead of [200, 400, 600Hz,...] you would have data for something like e.g. [201, 402, 603Hz,...] and so on. Repeating this and merging the results one could "fill" much of the missing data from 200Hz up. This is not the case, however, and won't work this way.
Last edited:
It would be a pretty bad speaker to have nulls as sharp as those in the example so this is not really an issue in practice, only in esoteric arguments on web forums. As I said before these issues may make a very bad speaker look better, but they will not make a good speaker look better.
But thanks John. Nothing new to me, but I would never have written this much detail.
Complex exponentials are clearly the ideal set of basis functions as all impulses are made up of these functions. The FFT actually uses complex exponentials but the complex part of the frequency parameter is set to 0.0.
But thanks John. Nothing new to me, but I would never have written this much detail.
Complex exponentials are clearly the ideal set of basis functions as all impulses are made up of these functions. The FFT actually uses complex exponentials but the complex part of the frequency parameter is set to 0.0.
Last edited:
As I said before these issues may make a very bad speaker look better, but they will not make a good speaker look better.
That's exactly where the argument started. How can anybody tell from the measurement if the speaker is good or simply made to look better? Measurements should remove doubts not reinforce them.
Markus,
The bottom line from your point of view is that you can never trust any manufacturer's response curves. But that pretty much means you can never make any type of conclusions without doing all the testing yourself, and then who's to say that your testing is any more accurate? After awhile you can look at a frequency response plot and intuitively know that a frequency response curve has been intentionally smoothed. It isn't often that this doesn't happen for multiple reasons, the most common is that a real response curve with all the perturbations, the little high Q response peaks would make someone think the device under test was inferior to a smoothed response curve from another manufacturer. JBL has done it for years in published response plots and it is as easy as slowing down a strip chart recorder to smooth the response curve. There are also valid reasons to smooth a response curve when doing something like a polar plot as it is easier to see trends and slight modifications that you are trying during development. Some companies print very detailed response curves on individual drivers and here you can see all the small details, warts and all. I have no reason to believe that Earl needs to fudge his response curves but understand that there may be some smoothing involved. I imagine that the type of graphic display that Earl uses would get rather messy to look at if he did not do something.
The bottom line from your point of view is that you can never trust any manufacturer's response curves. But that pretty much means you can never make any type of conclusions without doing all the testing yourself, and then who's to say that your testing is any more accurate? After awhile you can look at a frequency response plot and intuitively know that a frequency response curve has been intentionally smoothed. It isn't often that this doesn't happen for multiple reasons, the most common is that a real response curve with all the perturbations, the little high Q response peaks would make someone think the device under test was inferior to a smoothed response curve from another manufacturer. JBL has done it for years in published response plots and it is as easy as slowing down a strip chart recorder to smooth the response curve. There are also valid reasons to smooth a response curve when doing something like a polar plot as it is easier to see trends and slight modifications that you are trying during development. Some companies print very detailed response curves on individual drivers and here you can see all the small details, warts and all. I have no reason to believe that Earl needs to fudge his response curves but understand that there may be some smoothing involved. I imagine that the type of graphic display that Earl uses would get rather messy to look at if he did not do something.
^
The argument is simply about what measurements show and what not. Windowed data hides detail. Is the amount of detail necessary? Anechoic data without any gating applied would tell. It's simple as that.
I've never said Earl would fudge his speaker data nor do I think he would need to (I've measured them). He shows details virtually nobody else does. Nevertheless he gives an interpreted view on his speakers, just like everybody else does.
Again, I would like to be able to look at unsmoothed anechoic data. That data could be made available by manufacturers.
For example, Tom has his speakers tested by a third party. The resulting data is then published in a standardized format that is useful for certain applications. Unfortunately the data is smoothed before it gets published (1/3 octave I believe). I would like to be able to download the impulse responses of the single measurements. This is doable and the data is there. They just refuse to publish it, just like Harman refuses to publish their anechoic data.
The argument is simply about what measurements show and what not. Windowed data hides detail. Is the amount of detail necessary? Anechoic data without any gating applied would tell. It's simple as that.
I've never said Earl would fudge his speaker data nor do I think he would need to (I've measured them). He shows details virtually nobody else does. Nevertheless he gives an interpreted view on his speakers, just like everybody else does.
Again, I would like to be able to look at unsmoothed anechoic data. That data could be made available by manufacturers.
For example, Tom has his speakers tested by a third party. The resulting data is then published in a standardized format that is useful for certain applications. Unfortunately the data is smoothed before it gets published (1/3 octave I believe). I would like to be able to download the impulse responses of the single measurements. This is doable and the data is there. They just refuse to publish it, just like Harman refuses to publish their anechoic data.
Last edited:
Again, I would like to be able to look at unsmoothed anechoic data. That data could be made available by manufacturers.
Good luck with that!
The reason is because people (not YOU of course) WOULD take advantage and publish misleading and embarrassing things from the data. As bad as manufacturers might be, customers and competitors are worse!
The most that I got from all the ranting here is that the impulse response should be shown so that it is obvious that truncation has not chopped off anything of significance.
Last edited:
The reason is because people (not YOU of course) WOULD take advantage and publish misleading and embarrassing things from the data.
That would happen in the beginning but it is my belief that the lack of information is the problem, not its availability. Isn't that what science is all about??
Yes, but even with the most admirable of intentions, designing and selling speakers is done to make money and provide consumers with good speakers, not to provide data to scientists.
It is most unfortunate that the honest speaker salesman is considered the bad guy because it is believed that his only motivation is greed. The concept that he may actually believe in what he is doing because he provided a quality product at a reasonable price gets lost.
In audio "ignorance is bliss" (and good for marketing as well!)
In audio "ignorance is bliss" (and good for marketing as well!)
This is deflecting from the real point of the thread, which is the effect of gating on the resolution of the frequency response. JohnPM's post clearly shows all the effects. The only debate is whether the resolution is enough or not.
Soundstage does a good job of anechoic measurements. Love their data.
SoundStageNetwork.com | SoundStage.com | SoundStageNetwork.com | SoundStage.com
Soundstage does a good job of anechoic measurements. Love their data.
SoundStageNetwork.com | SoundStage.com | SoundStageNetwork.com | SoundStage.com
It is most unfortunate that the honest speaker salesman is considered the bad guy because it is believed that his only motivation is greed.
That's a misconception.
- Status
- Not open for further replies.
- Home
- Loudspeakers
- Multi-Way
- FFT windowing and frequency response resolution