try root 2
almost every question you have asked recently has been answered before.
Have you tried using google to search?
LMGTFY
As Globalplayer says, one nice thing about using 1.618 is that as a free bonus, you also get reasonably pleasing shapes. Though it's also true that I personally happen to find ratios a bit less than 1.618 often look more pleasant to my eyes.
I think all we can hope for is to keep the lowest few acoustic resonance modes from falling close enough to each other to reinforce themselves. Further up in frequency, it doesn't matter what ratios your enclosure has, there are so many tightly-spaced resonance peaks that some are bound to have unfavourable frequency relationships.
So we can only hope that at these higher frequencies the acoustic treatment we used inside the enclosure is doing a good job of absorbing sound and lowering the Q of that forest of resonant modes sufficiently to keep them from being annoying.
Interestingly, two of the least boxy-sounding instrument amplifiers I've heard have enclosures that are not simple right rectangular prisms. In fact, only two side walls are parallel in these enclosures.
Contrary to popular belief, non-rectangular speaker enclosures have internal resonant acoustic modes too, though they are harder to calculate. But they are usually not equally spaced in frequency, the way the modes of a right rectangular prism are.
I don't know whether it is the non-uniform frequency spacing that makes these particular speakers sound less "boxy", or whether there are actually fewer resonant modes in the frequency band of interest. But, for whatever reason, these non-rectangular enclosures do seem to produce less audible "boxiness".
Then again, I've heard several nearfield monitor speakers aimed at the home studio that manage not to sound boxy, even though they are more or less right rectangular prisms. With reasonable edge dimensions and lots of good quality acoustic fill, apparently it's possible to reduce boxiness to the point where it's not particularly noticeable.
-Gnobuddy
Picking any irrational number won't necessarily be as good as the golden ratio.
For instance, 3/5 or 5/3 isn't great because both 3 and 5 are reasonably small integers. Consider that an enclosure panel has natural resonant frequencies determined by it's length and width but it also resonates at multiples/harmonics of these frequencies. If you make two dimensions of the enclosure have a ratio of 3:5, the 5th harmonic across the '3' dimension is at the exact same frequency as the 3rd harmonic across the '5' dimension. Instead of achieving a 'noise floor' of lots of different frequencies they start piling on top of each other leading to a smaller quantity of more severe resonances.
As you can imagine, 1:1 is the worst case, followed by 1:2. 2:1, 2:3, 3:2, 1:3, 3:1 etc.
Obviously, picking a ratio like 279:278 isn't great either because while the numbers have a high order, it's practically the same as 1:1 since panel resonances have a finite Q and still effectively pile on top of each other (within a few %).
Using the golden ratio ensures a fairly "spread spectrum" effect on resonances and standing waves because it takes quite a high order before the multiples of each land on the same numbers, and higher order modes are typically much attenuated.
For instance, 3/5 or 5/3 isn't great because both 3 and 5 are reasonably small integers. Consider that an enclosure panel has natural resonant frequencies determined by it's length and width but it also resonates at multiples/harmonics of these frequencies. If you make two dimensions of the enclosure have a ratio of 3:5, the 5th harmonic across the '3' dimension is at the exact same frequency as the 3rd harmonic across the '5' dimension. Instead of achieving a 'noise floor' of lots of different frequencies they start piling on top of each other leading to a smaller quantity of more severe resonances.
As you can imagine, 1:1 is the worst case, followed by 1:2. 2:1, 2:3, 3:2, 1:3, 3:1 etc.
Obviously, picking a ratio like 279:278 isn't great either because while the numbers have a high order, it's practically the same as 1:1 since panel resonances have a finite Q and still effectively pile on top of each other (within a few %).
Using the golden ratio ensures a fairly "spread spectrum" effect on resonances and standing waves because it takes quite a high order before the multiples of each land on the same numbers, and higher order modes are typically much attenuated.
Last edited:
Note that 3/5 and 5/3 are not irrational numbers. In fact, the definition of an irrational number is that it cannot be expressed as a ratio of two integers! ( Irrational Numbers )
A clue is contained in the decimal representation: if the digits start to repeat, then it is not irrational. For example, 1.11111... is not irrational (in fact it's 10/9). The same goes for 1.6666...., which is 5/3
Some well-known irrational numbers include the Golden Ratio (sometimes referred to as the Greek letter phi) which is roughly 1.618, the square root of 2, which is roughly 1.414, and pi, which is roughly 3.142.
We know that a speaker enclosure with dimensions in ratios like 3:5 is not a great idea (these are rational numbers.) People recommend the irrational Golden Ratio, phi:1. But what about (square root of two):1, or pi:1? I believe that was the OPs original question.
In practical terms, we cannot hope for construction accuracy to dozens of decimal places, so we will never achieve a true irrational number. With typical DIY construction accuracy I don't know if we can do much better than the 3rd decimal place (this would require wood thickness be accurate to 1 mm for a metre-long enclosure, which is a tall order.) I suspect we are often only accurate to the 2nd decimal place or a little better.
This means if you go high enough in frequency, there will be no practical difference between a speaker box with a ratio of the irrational number pi:1, and a box with a ratio of 22:7 (which is the same as pi for the first two decimal places).
As I said in post #11, I think that this means we really only need to worry about the lowest few modes, maybe ten. Beyond that, all we can hope for is to attenuate the heck out of them with acoustic fill.
So the real question is: Given that we're only accurate to maybe 2 or at best 3 decimal places, and only care about the lowest ten or twenty modes, what mathematical ratios give us the best spacing of resonant modes?
I don't know the answer. In particular I don't know if (phi:1) is really any better than (any other irrational number:1).
We have also been ignoring the third dimension of the enclosure so far. Really we want (phi*phi : phi : 1), or (pi * pi : pi : 1), etc.
-Gnobuddy
I wonder what the depth ratio was given by the "optimum" box size button in the old WinISD beta? Will have to go look.
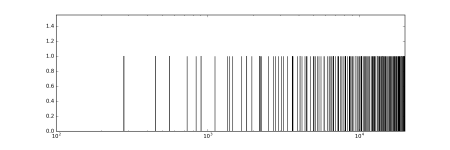
I have the day off, so I spent a little time writing a little Python program to calculate all the x,y,&z resonant frequencies of a box 24" long on the longest dimension, with all three sides in the Golden Ratio. (Divide 24 by phi to get the next smaller side, divide that by phi to get the smallest.)
The result is attached.
It does not look good - there is an absolute forest of modes, especially at the high-frequency end of the plot. (Plotted from 100 Hz to 20 kHz, because there are no modes below 100 Hz.)
Note that the plot assumes infinite Q for each mode, and that all frequencies exactly follow the very simple mathematical series you see in elementary textbooks. Quite likely, in real life, higher frequency modes will be shifted a little from the simplest theoretical approximation.
-Gnobuddy
The result is attached.
It does not look good - there is an absolute forest of modes, especially at the high-frequency end of the plot. (Plotted from 100 Hz to 20 kHz, because there are no modes below 100 Hz.)
Note that the plot assumes infinite Q for each mode, and that all frequencies exactly follow the very simple mathematical series you see in elementary textbooks. Quite likely, in real life, higher frequency modes will be shifted a little from the simplest theoretical approximation.
-Gnobuddy
Attachments
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.