youngho, no, I was talking about the rate after the initial drop. Looking at the picture Todd posted, the line on the left hand side decays faster than that on the right side. In the first few ms there's a huge drop but we still do not know if this is enough to render the ringing inaudible.
Todd offers an explanation:
But doesn't this bring us back to my initial comment that I've never seen a CSD that clearly shows that an EQ completely eliminated ringing?
Todd offers an explanation:
But doesn't this bring us back to my initial comment that I've never seen a CSD that clearly shows that an EQ completely eliminated ringing?
markus76 said:
Hmm, it goes to zero on the right earlier, no? It decays faster on the right initially, then it seems to decay more slowly after that, but it reaches zero earlier. And shouldn't inaudible should be at the level of the noise floor?
Oops, sorry, not a physicist or an engineer. I'l shut up now.
markus76 said:
It should be inaudible if the noise floor is inaudibleI think the data shown isn't very clear, but it was not me that asserted that "This [data] is not hard to find."
Just out of curiosity, how would this "modal ringing" be audible above the noise floor, i.e. the "room ringing"? And the graphs were in the book! I was about to refer you to page two-hundred-forty-whatever, myself.
john k... said:
John
Agreed! With one caveat. The function X(r) will be different for every source position in the room. There is no single X(r) that will satisfy the boundary conditions for an arbitray source location.
When Morse subtracts off the near field from the Green's function G(r) he does this by only fitting the singularity at the source point. This approach is then only approximate at the walls, but more accurate at the source than the series, because it converges faster. This leaves X(r) independent of the source location, BUT it is only an approximate solution.
markus76 said:
It should be inaudible if the noise floor is inaudible
I could definately find more, but it is time consuming. If yo have access to the AES journal, you should find more. And in any case I agree that the waterfalls are often hard to read/interpret.
Here's one I measured myself, a resonance at 28 Hz, no eq and eq.
Attachments
gedlee said:
I think the problem is the way Morse write the relationship
G(R,Ro) = g(R,Ro) + X(R)
This says X(R) = G(R,Ro) -g(R,Ro) .
Obviously X is a function of Ro. However, X(R) is a solution to (here we go again) the homogeneous wave equation with inhomogeneous boundary conditions (finally got that right). This is were the dependents of X(R) on Ro comes in because the boundary conditions are dependent upon the value of g(R,Ro) evaluated on the bounding surfaces. So while the dependence of X on Ro is not explicit, there is implicit dependence of X on Ro from the BC's. Perhaps it would have been better if Morse had written X(R) is a solution to the homogeneous wave equation with inhomogeneous boundary conditions, BC = F(g(Rb,Ro)) where Rb is the position vector defining the bounding surface. Change the source position and the X changes as well.
I guess I saying that I'm not particularly worried about what Morse says he does or doesn't do. If I have G(R,Ro) and I know g(R,Ro) I can drop in the values of R and Ro and find the value of X (R) for any values of R and Ro in the bounded region. But it's all academic because there is no need to worry about X if we know G(R,Ro).
On the effect of EQ on decay rate
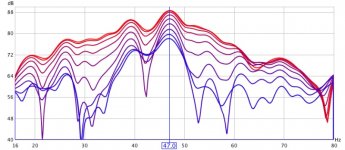
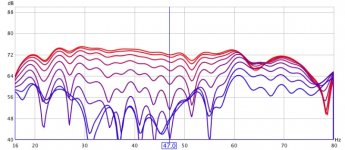
By courtesy of the Anti-Mode 8033 subwoofer EQ developer I'm posting a before/after comparison of what the aforementioned little box can do with regards to the decay rate of LF modes.
The time slices are 20 ms each, so from 0-160 ms. The comparison clearly shows faster rate of decay, at least up to 160 ms.
By courtesy of the Anti-Mode 8033 subwoofer EQ developer I'm posting a before/after comparison of what the aforementioned little box can do with regards to the decay rate of LF modes.
The time slices are 20 ms each, so from 0-160 ms. The comparison clearly shows faster rate of decay, at least up to 160 ms.
Attachments
john k... said:
John
Agreed. I had always viewed this subtraction of the direct field as approximate at the boundaries, never exact. I think that's the part that may be getting lost. You are correct that G(r,r0) is exact and what is needed, it just converges very slow near the source. I suppose that one could use the near field term for points close to the source, but drop it further out. This would work if the source is not too close to a boundary. If the source is close to a boundary then using an image source or sources would work as the combination is always zero at the boundary.
