In practice the equations are not solved with Cramer, too inefficient.
So presumably there is a reason to use Cramer in the theory.
But the rationale behind Cramer's rule was never clear to me, I should have paid more attention in class.
I don't have any "feel" for the result, it just looks like a trick.
But I expect there should be some physical interpretation, I will study it a bit more.
I only have Wai-Kai Chen's book 'Linear Networks and Systems', I will try to find a copy of 'Active Network analysis'.
So thank you for the input, welcome to DIYaudio.
Best wishes
David
Dave, Have been thinking about your question on determinants and physical interp. I cannot see one. It is algebra at its worst-- it drives the solution away from any factored pole/zero result. Will be keeping track of this thread for any insight from the commuity. Thanks for throwing it out. I have seen some of Chen's work and that of John Choma. I thought they worked too much in the math domain where the circuit is forgotten. That is the appeal of the flow graph to me. The circuit is still in the picture.
Regards,
Auggie
Regards,
Auggie
Nor I yet.
But a gain is a ratio, of an input to an output, physically understandable.
The matrix method has the gain as a ratio, of two determinants, it seems there should be a physical interpretation.
Mason does briefly mention the physical interpretation of determinants as applied to flow graphs.
Yes, my reread of Mason showed the map was not as inevitable as I had believed, depends on the variables chosen to be modeled.
DPIs as the chosen variables seems to lead to a Flow graph that is easy to relate to the circuit.
But also has an obvious relation to the nodal admittance matrix so the determinant should have an interpretation.
Maybe a question for Dr Cherry once I collect my ideas a bit more coherently.
Best wishes for the holidays
David
The matrices have admittance elements, each with units of current/voltage.
The units of the matrix determinant are (current/voltage)^n, where n is the order of the matrix.
Then the ratio of two matrices can have units of impedance,
admittance, or gain (pure number), depending on whether the order of the
two matrices is the same, or differs by one.
If the two matrices have the same order, then the units of the matrix ratio
is a pure number (or gain), since the units of the ratio are: [(i/v)^n / (i/v)^n] = 1.
If the numerator matrix has an order one smaller than the denominator matrix,
the ratio has the units of 1/(current/voltage), which is impedance.
The units of this ratio are: [(i/v)^n / (i/v)^(n+1)] = [1 / (i/v)] = (v/i), or impedance.
Last edited:
Yes, that's more or less what I wrote back in post #39 - "actually units are = admittance^n for circuit with n nodes"
*To be pedantic that should be "Then the ratio of two matrix determinants...".
Thank you for the broader viewpoint, I had only considered the loop gain case where the matrices are the same size, not where the two matrices are different.
I think Bode uses this when he defines transfer functions from node i to node j then points out that this is formally defined even if i = j and discusses the interpretation.
But what is the interpretation of the actual determinant?
Best wishes
David
In a geometrical interpretation, the determinant of an nxn matrix is the magnitude of a volume
in n-vector space.
Yes, that's what I learned in my Maths course.
But what is the physical interpretation of an "n-dimensional admittance volume"?
And Bode also works with the mesh formulation, so the matrices are different and the determinants are "n-dimensional impedance volumes".
But they both provide the correct answer so there must be some deeper structure that I don't quite understand.
Best wishes for the holidays
David
With Ohm's law, both I=(1/R)V and V=IR work. There isn't a deeper structure, but an arbitrary choice
of how you write the equations, which then form the matrices. The same information is present in both cases,
but in different forms.
No surprise that an impedance or admittance formulation will work.
Of course a scalar admittance is just the inverse of an impedance.
For a network I am not so sure, I don't think the matrices are simply inverses(?)
But is the admittance determinant the simple inverse of the impedance determinant?
I suspect so but don't see what structure ensures this will happen.
Best wishes
David
Matrix algebra shows that Z = Y^-1 and Y = Z^-1 (that they are inverses of each other).
We have (1) V = Z I and (2) I = Y V
Then from (2): Y^-1 I = Y^-1 (Y V) = (Y^-1 Y) V = V
Then since Y^-1 I = V and from (1) V = Z I, we see that Y^-1 = Z.
We can also show the relation of detY and detZ,
since from matrix theory we know that det(A B) = detA detB.
If we let B = A^-1, then det(A A^-1) = detA detA^-1
and since det(A A^-1) = detI = 1, we have 1 = detA det A^-1
or detA^-1 = 1/ detA.
In our case let A = Y, then detY^-1 = 1/ detY,
and since Y^-1 = Z (from above), we then have detZ = 1/ detY.
Last edited:
Simple, the determinant of an NxN matrix it's the volume of an N-dimensional parallelepiped build using the ket vectors from the original matrix. The Hadamard inequality further justifies the analogy.
Now if you consider the linear operator to matrix isomorphism, you'll find out that the determinant is the volume that includes all possible trajectories of the linear operator in the N-dimensional phase space.
If the Z and Y matrices are indeed inverses then the rest is obvious, but I am not convinced of this yet, hence my concerns.
Consider a specific network with the admittance matrix defined in the usual way, for nodes from Kirchoff current law.
It is presumably possible to invert that admittance matrix and produce a matrix with units of impedance but I believe this is not the usual impedance matrix, which is derived from the network mesh and Kirchoff potential law.
Excellent motivation to reread W K Chen and Bode, do you have any additional references you recommend to explain your view?
Best wishes
David
Hi Waly
Yes, we already mentioned the geometrical interpretation of the determinant.
But what is the physical interpretation of a N-volume in admittances?
Best wishes for the season
David
Experiment with LTspice.
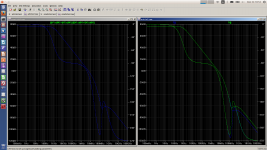
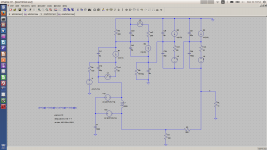
I did the simulation method which Ochoa describes in his book at page 95 and compared it with the GFT and Tians result.
For the GFT and Tians simulation, I used the LTspice implementation from
Frank Wiedmann https://sites.google.com/site/frankwiedmann/loopgain GFT_LTspice.zip .
(You can show Tians loop gain with Tt() ).
The circuit used is article2.asc, which shows a small difference between
Tian and Middlebrook.
The result of the simulation of Ochoa and Tian matches.
Well, this is not surprising, but nice to see it in a simulation.
Best wishes
Josef
I did the simulation method which Ochoa describes in his book at page 95 and compared it with the GFT and Tians result.
For the GFT and Tians simulation, I used the LTspice implementation from
Frank Wiedmann https://sites.google.com/site/frankwiedmann/loopgain GFT_LTspice.zip .
(You can show Tians loop gain with Tt() ).
The circuit used is article2.asc, which shows a small difference between
Tian and Middlebrook.
The result of the simulation of Ochoa and Tian matches.
Well, this is not surprising, but nice to see it in a simulation.
Best wishes
Josef
Attachments
Exactly as in |I>=|Y||U>, it's called the Ohm's law (|*> ket vector, |*| matrix).
You missed the second half of my post, forget for a second about matrixes and determinants and think in terms of a Nth grade linear differential equation associated to a circuit, as a result of applying the electrodynamics laws in differential format, the linear differential operator has a unique associated NxN matrix (it's called an isomorphism), jw->d/dt if you prefer. The determinant associated with the linear differential operator matrix is the volume occupied by all possible solutions for the linear differential equation in the phase space. Otherwise said, an arbitrary solution for the linear differential equation will always be inside of that volume. The boundary conditions for the differential equation (or node voltages, in the ket vector interpretation) are defining the particular solution for the circuit.
Exactly as you say, no surprise that it confirms Dr Ochoa's and my assessment, but nicely done, so thanks.
Best wishes
David
Didn't miss it, just don't see that it adds much.
But perhaps I did miss some implications, will think it over more, reply then.
Best wishes
David
Ok, have an answer for this, a simple example demonstrates that the usual network admittance matrix is not the inverse of the usual network impedance matrix.
But my suspicion in the first post was incorrect.
The determinants are not simply inverses.
David
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.