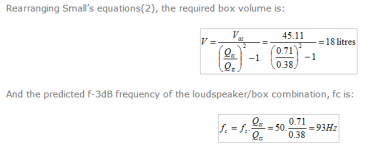In books such as The Loudspeaker Design Cookbook by Dickason and that book by Weems, Designing, Building, and Testing...., I've seen the formula
Qtc = ((Vas/ Vb) + 1)^2 *Qts
However, I was wondering if putting a driver in a closed box only increased Qm or only increased Qe or both. Intuitively it would seem correct to suppose that Qe would remain the same and Qm would increase. That's my intuition, as putting the driver in a closed box isn't changing anything electrical, but only the mechanical side of its operation.
Then I manipulated some equations by Thiele in a paper of his to discover that
Qec = ((Vas/ Vb) + 1)^2 * Qes
Qmc = ((Vas/Vb) +1)^2 * Qms
This being in agreement with the standard equation relating Qts to Qtc that I started with.
Would all of you in the know with T/S calculations agree with my equations for Qec and Qmc?
Why should Qe change when the electrical condition of the driver is unchanged?
Qtc = ((Vas/ Vb) + 1)^2 *Qts
However, I was wondering if putting a driver in a closed box only increased Qm or only increased Qe or both. Intuitively it would seem correct to suppose that Qe would remain the same and Qm would increase. That's my intuition, as putting the driver in a closed box isn't changing anything electrical, but only the mechanical side of its operation.
Then I manipulated some equations by Thiele in a paper of his to discover that
Qec = ((Vas/ Vb) + 1)^2 * Qes
Qmc = ((Vas/Vb) +1)^2 * Qms
This being in agreement with the standard equation relating Qts to Qtc that I started with.
Would all of you in the know with T/S calculations agree with my equations for Qec and Qmc?
Why should Qe change when the electrical condition of the driver is unchanged?
correction to equations
Sorry! -to all those who have looked at this. The equations are incorrect, I used the wrong symbolism for square root. The correct equations for Qec and Qmc are:
Qec = sqrt((Vas/Vb) +1) * Qes
Qmc = sqrt((Vas/Vb) +1) * Qms
Rather than reply to my own post, I did try to be able to edit my post, but was unsuccessful for what reason I don't know.
-Pete
Sorry! -to all those who have looked at this. The equations are incorrect, I used the wrong symbolism for square root. The correct equations for Qec and Qmc are:
Qec = sqrt((Vas/Vb) +1) * Qes
Qmc = sqrt((Vas/Vb) +1) * Qms
Rather than reply to my own post, I did try to be able to edit my post, but was unsuccessful for what reason I don't know.
-Pete
In terms of mechanical parameters
Qms = (1/Rms) x sqrt(Mms/Cms)
When placed in a box Cms is replaced by the combination of Cms in parallel with Cb, where Cb is the compliance of the box.
Similarly,
Qes = (Re/Bl)^2 x sqrt(Mms/Cms)
Again, in a box Cms must be replaced with Cms in parallel with Cb.
Since Cb in parallel with Cms is always less that Cms, both Qes and Qms increase by sqrt(Cms/Cab) where
Cab = Cb x Cms /(Cb + Cms)
If you work through the math,
Sqrt(Cms/Cab) = Sqrt( (Cb + Cms)/Cb) = Sqrt(1 + Cms/Cb) = sqrt(1 + alpha).
------
Alpha = Vas/Vb.
Since
Vas = Sd^2 x Cms x const.
and
Vb = Sd^2 x Cb x const.
Cms/Cb = Vas/ Vb = alpha.
The bottom line is that both Qe and Qm increase by a factor of
Sqrt(1 + alpha), as does Qt because of the change in compliance.
Qms = (1/Rms) x sqrt(Mms/Cms)
When placed in a box Cms is replaced by the combination of Cms in parallel with Cb, where Cb is the compliance of the box.
Similarly,
Qes = (Re/Bl)^2 x sqrt(Mms/Cms)
Again, in a box Cms must be replaced with Cms in parallel with Cb.
Since Cb in parallel with Cms is always less that Cms, both Qes and Qms increase by sqrt(Cms/Cab) where
Cab = Cb x Cms /(Cb + Cms)
If you work through the math,
Sqrt(Cms/Cab) = Sqrt( (Cb + Cms)/Cb) = Sqrt(1 + Cms/Cb) = sqrt(1 + alpha).
------
Alpha = Vas/Vb.
Since
Vas = Sd^2 x Cms x const.
and
Vb = Sd^2 x Cb x const.
Cms/Cb = Vas/ Vb = alpha.
The bottom line is that both Qe and Qm increase by a factor of
Sqrt(1 + alpha), as does Qt because of the change in compliance.
Okay, so it DOES seem reasonable that decreasing compliance by back loading the driver with a closed box would increase Qm. But it DOES NOT seem reasonable at all that decreased compliance would increase Qe. Is this perhaps a case of Thiele/ Small as a simplication becoming stretched?
Now, I'm not going to lose sleep if this doesn't become reasonable. I'm just exercising my curiosity here.
Thanks for confirming my "discovery", anyway.
Thanks to Ron for the info about editing.
I did neglect to edit my first equation relating Qtc to Qts. I'll do that now just to make this more worthy of the archive.
Qtc = sqrt((Vas/ Vb) + 1) * Qts
Regards,
Pete
Now, I'm not going to lose sleep if this doesn't become reasonable. I'm just exercising my curiosity here.
Thanks for confirming my "discovery", anyway.
Thanks to Ron for the info about editing.
I did neglect to edit my first equation relating Qtc to Qts. I'll do that now just to make this more worthy of the archive.
Qtc = sqrt((Vas/ Vb) + 1) * Qts
Regards,
Pete
MCPete said:Is this perhaps a case of Thiele/ Small as a simplication becoming stretched?
No. Thiele small theory neglects radiation resistance, assumes the elements can be lumped and ignores changes in parameters with level and frequency, but still predicts your "discovery".
John proved both Qes and Qms are modified by compliance (the only variable which affects Fs). This is why I put my answer in terms of Fs - most never get past Fs, Qts, Vas modeling...
MCPete said:Okay, so it DOES seem reasonable that decreasing compliance by back loading the driver with a closed box would increase Qm. But it DOES NOT seem reasonable at all that decreased compliance would increase Qe. Is this perhaps a case of Thiele/ Small as a simplication becoming stretched?
Now, I'm not going to lose sleep if this doesn't become reasonable. I'm just exercising my curiosity here.
Thanks for confirming my "discovery", anyway.
Thanks to Ron for the info about editing.
I did neglect to edit my first equation relating Qtc to Qts. I'll do that now just to make this more worthy of the archive.
Qtc = sqrt((Vas/ Vb) + 1) * Qts
Regards,
Pete
Well you just have to look at the definitions of Qe and Qm. Both depend on moving mass and total compliance. The differences is that Qm includes mechanical damping and Qe electrical damping. As Ron noted eariler, the electrical damping doesn't change. Neither does the mechanical damping. Also note that Q is not just damping. It is actually a ratio of the ability to store energy to the ability to dissapate energy. You should be able to grasp that a stiffer spring can store more energy than a weak one. Thus when the compliance decreases Q increases because the system can store more energy.
Qm and Qe come directly out of the equation which governs the motion of the cone.
Yes, I see in John K's post that both Qes and Qms are directly proportional to sqrt(Mms/ Cms). But these are equations devised by Thiele and Small that define what Qes and Qms are. So merely stating their equations doesn't answer my question.
In other words Thiele and Small understood a connection between compliance and electrical Q. The equation for Qes states the connection, but the equation by itself doesn't provide any explanation as to why there is a connection.
In the case of Qms, Qms directly proportional to stiffness is fairly easy to comprehend. A spring with increased tension can store and release more energy as a result of being made more stiff.
But WhY should compliance affect electrical Q? Given the sophistication of the authors of these equations, I would think that there probably is an explainable link between electrical Q and compliance. -That is what I would maybe like to be able to grasp so long as it doesn't require being able to do Calculus.
-Pete
In other words Thiele and Small understood a connection between compliance and electrical Q. The equation for Qes states the connection, but the equation by itself doesn't provide any explanation as to why there is a connection.
In the case of Qms, Qms directly proportional to stiffness is fairly easy to comprehend. A spring with increased tension can store and release more energy as a result of being made more stiff.
But WhY should compliance affect electrical Q? Given the sophistication of the authors of these equations, I would think that there probably is an explainable link between electrical Q and compliance. -That is what I would maybe like to be able to grasp so long as it doesn't require being able to do Calculus.
-Pete
MCPete said:But WhY should compliance affect electrical Q? Given the sophistication of the authors of these equations, I would think that there probably is an explainable link between electrical Q and compliance.
What happens with a coil of wire when you move it through a magnetic field? What happens if you move it faster (Higher Fs)?
What you are missing is that Q applies or is calculated at resonance. But first, consider the definition of resonance, it is when the positive and negative reactances are of equal magnitude so that they exactly cancel and there is no imaginary part in the total impedance. If you alter the total compliance the resonance will shift to a frequency where the reactance of the mass is equal to that of the new total compliance. The reactances were equal and of one magnitude at the free air resonance, and equal but of a different magnitude at the closed box resonance. Now, Q is the ratio of reactance over resistance at resonance, the reactance changed, the electrical damping did not, but obviously the Q does change.
Remember that for damping purposes you can short the voltage source, then pull the source resistance through the gyrator (representing the driver motor) into the mechanical secondary circuit of the driver for analysis.
I suggest that you look up the equations for the impedance of a mass, and compliance.
Qm is simply expressing the mechanical restance as a ratio to reactance at resonance.
Qe expresses the electrical damping resistance as a ratio.
And Qt combines Qm and Qe to express the combined resistive damping as a ratio.
Pete B.
Remember that for damping purposes you can short the voltage source, then pull the source resistance through the gyrator (representing the driver motor) into the mechanical secondary circuit of the driver for analysis.
I suggest that you look up the equations for the impedance of a mass, and compliance.
Qm is simply expressing the mechanical restance as a ratio to reactance at resonance.
Qe expresses the electrical damping resistance as a ratio.
And Qt combines Qm and Qe to express the combined resistive damping as a ratio.
Pete B.
MCPete said:Yes, I see in John K's post that both Qes and Qms are directly proportional to sqrt(Mms/ Cms). But these are equations devised by Thiele and Small that define what Qes and Qms are. So merely stating their equations doesn't answer my question.
In other words Thiele and Small understood a connection between compliance and electrical Q. The equation for Qes states the connection, but the equation by itself doesn't provide any explanation as to why there is a connection.
In the case of Qms, Qms directly proportional to stiffness is fairly easy to comprehend. A spring with increased tension can store and release more energy as a result of being made more stiff.
But WhY should compliance affect electrical Q? Given the sophistication of the authors of these equations, I would think that there probably is an explainable link between electrical Q and compliance. -That is what I would maybe like to be able to grasp so long as it doesn't require being able to do Calculus.
-Pete
They are not equations derived by Thiele and Small, they come directly from the equation of motion for the cone. Probably too much detail but we start by writing that the sum of the forces on the cone = the acceleration of the cone (Newtons Law)
F - Rms x’ – C x = M x’’
where F is the applied force, Rms is mechanical resistance, C is compliance, M is moving mass. x = displacement, x' = velocity, x" = acceleration of the cone.
F = BL * I, the force generated in the motor,
But
I = (Es - Eb) /Re
where Es is the (amplifier) appled voltage , Eb is the back EMF and Re is the voice coil resistance. ( If you consider voice coil inductance we need to use Ze, but Le is not a significant contribution of Ze around resonance so we can use Re.)
The back EMF is
Eb = BL * x'
Thus
I = (Es - BL*x')/Re
The we can substitute and write,
(B L)(Es / Re) = m x’’ + (Rms + (B L)^2/Re) x’ + x / c
The term [Rms + (BL)^2/Re] is the damping term.
Now, this is recognized as a standard ordinary differential equation
F = Mx" + Bx' + Kx
for a 2nd order system which has a natural frequency,
wn = sqrt(K/M)
and
1/Q = B / sqrt(MK)
Comparing to out equation for the driver cone,
M = m,
K = 1/c
B = (Rms + (BL)^2/Re)
So
w = sqrt(mc)
1/Q = (Rms + (BL)^2/Re) / sqrt(m/c) = Rms/sqrt(m/c) + (BL)^2/Re)/ sqrt(m/c)
Or
1/Q = 1/Qm + 1/Qe
From whence we get the relations
Q = Qm * Qe / (Qm + Qe)
Again, the compliance,c, in the equation, is the total compliance (driver suspension plus box air spring).
Anyway, this is the basic analysis of the moving system and you should be able to see how the compliance enters into both Qm and Qe. What I showed before shows how the compliance terms changes when the air spring is included.
If you work through the math for the in box system you can write the equation as
F(t) = x” + Ù (1/Qms + 1/Qes) x’ + Ù^2 (1 + á) x
where Ù is an inverse dimensionless frequency, wn/w and á =Vas / Vbox.
There is nothing magical here. The dependence of Qm and Qe on compliance just comes out in the wash.
The reason to wrie the equation in dimensionless form is that it tells us about the relative effect of the different terms. For example, when w is small (very low frequency), Ù will be large, and the term Ù^2 (1 + á) x will dominate the other terms. This is the well know case where at low frequency the driver is controled by the compliance alone. When w is very large, Ù will be very small (and Ù ^2 even smaller) and the driver motion is dominated by the cone mass. This is the mass controled region where we have flat frequency response. When w is around wn, Ù will be about 1.0 and all three terms must be considered. The damping terms will be on the order of 1/Qm = 1/Qe = 1/Qt. So if Qt is very small, 1/Qt is very large and the damping will dominate around w = wn. If Qt is large, 1/Qt is small and damping drops out and we have an lightly oscillator with natural frequency = wn.
PB2 said:What you are missing is that Q applies or is calculated at resonance. I suggest that you look up the equations for the impedance of a mass, and compliance.
Aren't you the one with the question?
Impedance of a mass and compliance?
Mobility or impedance analogy?
Time for you to do your own homework.
Edit: Wondering what provoked this response ... My previous post was directed to the OP by the way, it is not all about you.
Are you trying to impress me?
Wow, you know the difference between an impedance and mobility analogy?
Yes, I am impressed with your rudeness! LOL!
I'm the one who answered the question here, does that bother you so much?
You need to do your homework, the Q is the same no matter which analogy you choose, LOL!
Yes, the internet is a nut house!
Are you trying to impress me?
Wow, you know the difference between an impedance and mobility analogy?
Yes, I am impressed with your rudeness! LOL!
I'm the one who answered the question here, does that bother you so much?
You need to do your homework, the Q is the same no matter which analogy you choose, LOL!
Yes, the internet is a nut house!
Ron E said:
What happens with a coil of wire when you move it through a magnetic field? What happens if you move it faster (Higher Fs)?
Oh, wait, perhaps it bothers you that this statement by you makes no sense what-so-ever, LOL!
People should also understand that T&S theory showed that a sealed box woofer is essentially a 2nd order high pass filter. This ignores the voice coil inductance which if high can result in some slope in the pass band, but this is easily accounted for on top of the basic 2nd order high pass view.
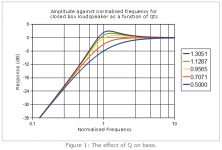
Consider what we call a prototype filter design, which is where we scale Fc to 1 Hz and the amplitude to 0 dB. Then we plot a family of filter responses as a function of Q. This would represent Qtc for a closed box, and Qts for free air operation. This family of curves represents any 2nd order speaker. Simply scale frequency by Fc, and shift the amplitude by making 0 dB the pass band sensitivity and pick the curve for the particular Qtc (or Qts). If you can picture the prototype family of curves then you now know every type of 2nd order or closed box system that can be built. Simple, anyone can do it.
Some Qtc values of particular interest are .5, .707, 1, and 2. I'll let people look them up to understand why.
Think, critically damped (-6dB at Fc), maximally flat (-3dB at Fc), 0dB output at Fc, and +6dB output at Fc.
One could also plot a family of transient response, say step response curves as a function of Qtc.
I'll let those learning look up the characteristics for some interesting Qtc values.
This is why Qts and Qtc are so interesting and important.
Pete B.
Consider what we call a prototype filter design, which is where we scale Fc to 1 Hz and the amplitude to 0 dB. Then we plot a family of filter responses as a function of Q. This would represent Qtc for a closed box, and Qts for free air operation. This family of curves represents any 2nd order speaker. Simply scale frequency by Fc, and shift the amplitude by making 0 dB the pass band sensitivity and pick the curve for the particular Qtc (or Qts). If you can picture the prototype family of curves then you now know every type of 2nd order or closed box system that can be built. Simple, anyone can do it.
Some Qtc values of particular interest are .5, .707, 1, and 2. I'll let people look them up to understand why.
Think, critically damped (-6dB at Fc), maximally flat (-3dB at Fc), 0dB output at Fc, and +6dB output at Fc.
One could also plot a family of transient response, say step response curves as a function of Qtc.
I'll let those learning look up the characteristics for some interesting Qtc values.
This is why Qts and Qtc are so interesting and important.
Pete B.
Hi in what proportion does Qtc/Qts change or is there any such ratio( since it depends on total damping and total compliance) because i agree that Qtco/Qts change with constant ratio of fc/fs.Your second set is correct.
Qxc/Qxs = Fc/Fs , so Q changes in proportion to the resonant frequency
Electrical damping is Bl^2/Re - unchanged
You can't edit because they lock posts for editing after perhaps 1/2 hour. They could leave it open, but choose not to.
sqrt(1+alpha) is the ratio, but in the real case, there are changes depending on how you measured T/S parameters, etc, and the compliance is level dependent and the damping terms are frequency dependent, etc.. You have to stop somewhere or else you will chase your tail forever...
There's a bit of a masterclass on closed box here at diyaudio by BBC engineer Morgan Jones:
http://www.diyaudio.com/forums/diyaudio-com-articles/158899-arpeggio-loudspeaker.html
He discusses how Qes is affected by single ended triode amplifier output impedance and resistance of bafflestep coils. And it contributes to Qts when added to Qms.
Typical 8" SEAS CA22RNX bass driver:
H1288-08 CA22RNX
But really the closed box formula is all you need. And a driver Qts of near 0.5 works best for closed box, which means smaller magnets than your usual reflex Qts 0.38 driver.
Then decide what sort of box Qtc you want. Anything over 0.71 sounds a bit one note IMO. It's also modified by room gain. Big freestanding speakers in small rooms sound over bassy IMO. Best reduce the bass and put them near the wall IMO.
http://www.diyaudio.com/forums/diyaudio-com-articles/158899-arpeggio-loudspeaker.html
He discusses how Qes is affected by single ended triode amplifier output impedance and resistance of bafflestep coils. And it contributes to Qts when added to Qms.
Typical 8" SEAS CA22RNX bass driver:
H1288-08 CA22RNX
But really the closed box formula is all you need. And a driver Qts of near 0.5 works best for closed box, which means smaller magnets than your usual reflex Qts 0.38 driver.
Then decide what sort of box Qtc you want. Anything over 0.71 sounds a bit one note IMO. It's also modified by room gain. Big freestanding speakers in small rooms sound over bassy IMO. Best reduce the bass and put them near the wall IMO.
Attachments
, and the compliance is level dependent and the damping terms are frequency dependent, etc.. You have to stop somewhere or else you will chase your tail forever...
I am lost here how is the compliance term level dependant
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.
- Home
- Loudspeakers
- Multi-Way
- Calculating Qec Qmc