Highest resolution without quantization noise

[Tattoo]

A 16-bit / 44.1 kHz file just like any other file except it's purely digitally encoded.

No, an AD converter has an anti aliasing filter before it in order to prevent frequencies above half the sampling frequency.

A digitally generated file can have frequencies above half the sampling frequency. If you don't take this into account aliasing will occur.
A good example is signal processing where non linear distortion is added to the signal. To prevent aliasing you need to upsample the signal enough, than add the non linear distortion, and then down sample again. That's why SY said you confuse recording with playback.

Its simple to test: If you have a DAW (audacity is free) you can create a square wave, witch looks perfect, and look at its spectrum. Result aliasing galore. Then record a square wave and study the differences. The recorded wave will not look perfect, because its band limited, but there's no aliasing.

Here's a great video demonstrating this at 17.20: D/A and A/D | Digital Show and Tell (Monty Montgomery @ xiph.org) - YouTube

 

[merlin el mago]

Dam I listen to music from the no-real reality, therefore I do not exist in the real reality I am just a figment of my imagination

You are welcome to non reality world.

 

[DF96]

"For example, 14-bit ADC can produce 16-bit 48 kHz audio if operated at 16x oversampling, or 768 kHz"

Only if the 14-bit ADC either has 16-bit accuracy or purely random errors. The latter is possible (depending on DAC architecture); the former is unlikely.

A 16-bit / 44.1 kHz file just like any other file except it's purely digitally encoded.

Such a file can contain data sequences which could not occur from a bandlimited source. This is a trick used by NOS fans to 'exhibit' the 'superiority' of their chosen nonfidelity.

 

[Tattoo]

Only if the 14-bit ADC either has 16-bit accuracy or purely random errors. The latter is possible (depending on DAC architecture); the former is unlikely.

Didn't the first Philips CD players have a 14 bit dac with 4 times oversampling and noise shaping. This got 16 bit resolution in the audio band.

 

[fotios]

Dam I listen to music from the no-real reality, therefore I do not exist in the real reality I am just a figment of my imagination

Knock, knock, Neo.

 

[godfrey]

A 16-bit / 44.1 kHz file just like any other file except it's purely digitally encoded.

Such a file can contain data sequences which could not occur from a bandlimited source.

I'm not convinced that's true. It seems to me that any such synthetically generated digital file could have been created by sampling some correctly band-limited analog signal.

My reasoning is as follows:
If you take that digital file and pass it through an ideal DAC with sinc interpolation, the resulting analog output will have no frequency components above fs/2. If you then sample that analog signal. the resulting digital data should be identical to what you started with.

The only quibble I see is that there may be content at exactly fs/2, in which case the amplitude is undefined. I'm not sure what sinc interpolation does with that.

 

[Tattoo]

My reasoning is as follows:
If you take that digital file and pass it through an ideal DAC with sinc interpolation, the resulting analog output will have no frequency components above fs/2.

It has now no frequencies above fs/2, but it has a LOT of aliasing artefacts.
Before you go into the dac, you have to make sure there are no frequencies above fs/2.

If you then sample that analog signal. the resulting digital data should be identical to what you started with.

No.

 

[sesebe]

Quote:
Originally Posted by DF96 View Post
Passive pre-filtering can slow the signal seen by the opamp down to the region where the opamp is well behaved.

Passive pre-filtering like what?

The op-amp is usually used as a low-pass filter, the article makes a case for the use of video op-amp's as LPF and that's very interesting!

Do you use some simulating tools?

Do a simulation of a low pass active filter of first order filter. Put on the input a step signal with a slew-rate of 1000V/µsec and measure the slew-rate at the inputs of the OP. After this post the results and comment!

This it is the schematic from wiki to not be confused: http://upload.wikimedia.org/wikipedia/commons/5/59/Active_Lowpass_Filter_RC.svg

 

[jcx]

Sampling theory, Nyquist doesn't say you can reproduce fs/2 content, only strictly less than that

another side of the box is amplitude - some bit patterns can give over 0 dB analog out - conversely would have required over 0 dB input analog signal in recording to get those bit patterns

 

[Kastor L]

With oversampling you can achieve the equivalent of 17-bit resolution or 102 dB.

However that is only the dynamic range to the quantization noise floor, it's still 96 dB even though it's stated as 102 dB.

Oversampling does not change resolution; it makes filter design easier.

"Remember the CD player numbers game? The first Philips-based machines had 14-bit, 4 times oversampling, the original Japanese used 16-bits. Then in 1986 the 16×4 Philips players arrived and by 1988 a raft of 18×8 machines appeared from the Orient. The Great Bit War seemed to be on in earnest, but then Philips launched Bitstream in 1989 and put a swift end to it
///
Dual Philips TDA 1541AS1 DAC's paired up and shared gave 18-bit resolution"

"The use of oversampling technology allowed the 16-bit Red Book standard to be met with the 14-bit DAC converters that were available when the system was introduced.

As well as allowing 16 bit-equivalent performance, this also offers additional benefits. For example, it gives a higher signal-to-noise ratio and higher dynamic range"

The way I see it oversampling moves the quantization error farther away thus increasing the depth to the quantization noise floor thus increasing the dynamic range.

If we increase 16-bit to a hypothetical 17-bit, like that, then the dynamic range is 102 dB and 96 dB at the same time.

The first one is quantization noise floor dynamic range, the second one is the musical dynamic range.

Yes?

 

[Kastor L]

A 16-bit / 44.1 kHz file just like any other file except it's purely digitally encoded.

An AD converter has an anti-aliasing filter before it in order to prevent frequencies above half the sampling frequency.

A digitally generated file can have frequencies above half the sampling frequency.

A 44.1 kHz file can not have frequencies above 44.1 kHz.

Let's say it does, just delete them then, wow, is it so difficult!

 

[Kastor L]

Linear phase reconstruction will look identical to the original.

Minimum phase reconstruction will look different.

I don't know about maximum phase. Is that ever used with DACs?

The point is, that reality is minimum-phase.

If someone strikes a cymbal 20 metres away, the air pocket which reaches you first is the tip of the drumstick connecting with the cymbal.

I.e. it's not the cymbal decay and then the strike a few milliseconds later.

If reality is minimum-phase then a reconstruction filter should be minimum-phase as well.

At the very least, the flagship DAC products from Wolfson and Asahi Kahei Microsystems entertain this.

The Cirrus Logic flagship DAC chip has a fast roll-off versus slow roll-off setting, not sure exactly how it's designed.

Maximum-phase is the inverse of minimum-phase and it would sound highly unnatural, in the situations when / if we could hear it.

Linear is halfway.

 

[Kastor L]

Do you use some simulating tools?

Do a simulation of a low pass active filter of first order filter. Put on the input a step signal with a slew-rate of 1000V/µsec and measure the slew-rate at the inputs of the OP. After this post the results and comment!

This it is the schematic from wiki to not be confused: http://upload.wikimedia.org/wikipedia/commons/5/59/Active_Lowpass_Filter_RC.svg

I don't use simulating tools sorry. I look at schematics a little such as in LTspice or the pictures at ZeptoBars.

I suspect the simulating tools will not take all the Mhz frequencies of the DAC chip into account.

From what I took from the article, the Mhz frequencies in DAC chips, as well as radio frequency interference, are incentives to use two video op-amp's in the pathway after it.

In a live simulation, what kind of results would you be interested in?

"The Texas Instruments / Burr-Brown PCM63 DAC generates a comb spectra, that is flat out to 20MHz and declines into the noise floor at 50MHz"

 

[Kastor L]

A few interesting links —

SRC Comparisons - Help and Information

http://www.wolfsonmicro.com/media/77050/Ultra_High_Performance_DAC_whitepaper.pdf

https://web.archive.org/web/2013120...-laser.com/technology/techsacd/techsacd14.htm

Accudio?

</title> <meta name=description content=""/> <meta name=keywords content=""/> <meta http-equiv=Content-Type content="text/html; charset=utf-8"/> <link rel=stylesheet type="text/css" href="/css/main.css?ez_orig=1"/> <link rel=stylesheet type="text/css

 

[benb]

I think most of those who know what they are talking about have already left the building.
It's all yours.

Jan

I've posted links (thinking of DSPguide and the NS dither app note) in earlier pposts but have got no response. I presume anyone who read them was already familiar with their content.

Here's another - this is more oriented to recording (and "mastering" which once meant the EQ and other stuff done for LP cutting) and so covers a lot of unrelated stuff, but the digital-recording parts such as bit depth and dither are relevant:
Audio FAQ - Digital Domain: CD Mastering | Mastered for iTunes | Audio Mastering | Blu-Ray Mastering

...
That is why DSD usually sounds better than CD's, the studios which use DSD are "paranoid" and use better microphones and ADC as well.

Remember that "garagerock" received it's name from being recorded in a garage.....

Most likely with not very good recording equipment......

Yet it still sounds pretty good imho, LoL.

I think that's an important point. LP's are making a minor resurgence, and I think some of it has to do with hearing an LP that was produced and presssed many decades ago that has wonderful dynamics and very little (compared to recent decades) compression, and the listeners think "Wow, I should get into LPs because they sound great, so much better than CDs and MP3s!"

People buy recorded music because of its emotional impact, not because of specs or equipment or medium, but often these things get confused. Admittedly, it's hard to separate them.

O.k., with shaped dither we can move noise away from the 2-4 kHz area.

However can the music signal then vary by 120 dB in the 2-4 kHz area as well, or is it still limited to a 96 dB ceiling?

Yes, and that's the point. In the 10-22 kHz range (or wherever the noise-shaping filter puts the most noise, somewhere in the high end of the audible spectrum), there is substantially LESS than 96kHz dynamic range, but (I think as someone else was sort-of saying), the ear isn't as sensitive to these frequencies at lower volume levels (see the Fletcher-Munson curve - it appears the threshold of hearing at 10kHz is +15dbSPL), so overall the noise floor sounds lower.

Noise-shaping actually reduces the measured dynamic range when considering all frequencies from 20Hz to 20KHz equally, but aurally the range is increased.

Sampling theory, Nyquist doesn't say you can reproduce fs/2 content, only strictly less than that

another side of the box is amplitude - some bit patterns can give over 0 dB analog out - conversely would have required over 0 dB input analog signal in recording to get those bit patterns

The processing and "hypercompression" done to the signals on many CDs released in the last couple of decades often does this, though I'm sure (ahem) no one in this thread listens to such CDs...

 

[Tattoo]

A 44.1 kHz file can not have frequencies above 44.1 kHz.

Let's say it does, just delete them then, wow, is it so difficult!

It does inside the digital system.
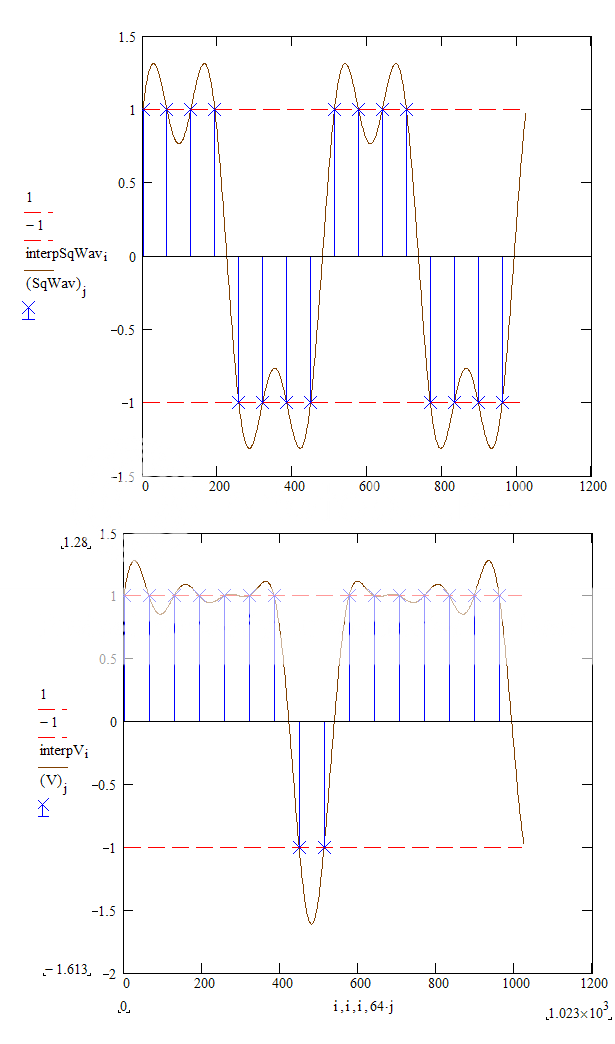
First, the sampling process creates square waves of 44,1kHz, with harmonics at 132.2kHz and so on These frequencies should be removed by a reconstruction filter, to prevent intermodulation artefacts in the audio band.

Second, if the sound ITSELF has frequencies above fs/2, for example by adding non linear distortion in the digital domain, then these frequencies will alias back into the audio. These aliasing products can not be filtered out by the reconstruction filter.
Iaw: If there are no frequencies above fs/2 in the signal present, then there is only 1 way to connect the sample values together. If there are frequencies above fs/2 in the signal present, then there is more than 1 way to connect the sample values and extra frequencies are generated: Aliasing.

To make this clear, I've made 2 soundfiles with my DAW. One 10kHz sine and one 10kHz square. If everything is fine then these files should sound the same. The first harmonic of the 10kHz square is at 30kHz and no human can hear that. (I hope we can all agree on that.) But as you can hear, the files sound very different and of cause the spectra looks very different to.

To hear the soundfiles change zip to wav.

 

[Tattoo]

The way I see it oversampling moves the quantization error farther away thus increasing the depth to the quantization noise floor thus increasing the dynamic range.

If we increase 16-bit to a hypothetical 17-bit, like that, then the dynamic range is 102 dB and 96 dB at the same time.

The first one is quantization noise floor dynamic range, the second one is the musical dynamic range.

Yes?

It works ONLY IF the noise of the oversampling is decorrelated, not so easy.
The first Philips CD players used oversampling in combination with noise shaping to get to 16 bit resolution in the audio band. Here the noise is shifted to frequencies above 20kHz, much easier to do.

 

[sesebe]

I don't use simulating tools sorry. I look at schematics a little such as in LTspice or the pictures at ZeptoBars

Big mistake. That way you could better understand the things that you say and maintain that you are the expert. But it is much easier to read bits of information out of context and then to claim that those are the real things.

Several years ago I had a serious dispute to work as if written on the internet something, especially on Wikipedia, it is true.
End dispute was simple. Another colleague was listed as author of Mona Lisa and then asked others to check on internet the author. Of course then made ​​the necessary correction but it was enough to convince other colleagues that the information from the internet are not always accurate.

I suspect the simulating tools will not take all the Mhz frequencies of the DAC chip into account.

From what I took from the article, the Mhz frequencies in DAC chips, as well as radio frequency interference, are incentives to use two video op-amp's in the pathway after it.

Not really. Intro simulation can be done more than is possible in real life, the only real limitation is only your imagination. So properly preparing a simulation, you can take into account the frequency and harmonics up beyond the sites GHz. That is not possible in real life.

In a live simulation, what kind of results would you be interested in?

You have seen the slew rate to entries in OP is much smaller (even over 100x lower) than the slew-rate of the entry in the filter.

 

[Kastor L]

LP's are making a minor resurgence, and I think some of it has to do with hearing an LP that was produced and pressed many decades ago that has wonderful dynamics and very little compression ///

Personally I think it's mostly the physical medium and the feeling of purchasing / collecting a limited edition vinyl.

As for the musical dynamic range, how about cassette tape, it's the same concept right.

Dynamic range - Wikipedia, the free encyclopedia

"Compact Cassette tape performance ranges from 50 to 56 dB depending on tape formulation"

Noise-shaping actually reduces the measured dynamic range when considering all frequencies from 20Hz to 20KHz equally, but aurally the range is increased.

Right, measured dynamic range versus aural dynamic range is another way of saying engineering dynamic range versus perceived dynamic range, which Abraxalito pointed out earlier.

However, these terms relate strictly to the noise floor.

The musical dynamic range has nothing to do with the noise floor, it's the softest note to the loudest note within the media file, I'm wondering if this can exceed 96 dB in 16-bit / 44.1 / 96 / 192 kHz L-PCM.

Likewise, if it can exceed 24 dB in 4-bit / 44.1 kHz.

To illustrate further, if a sound in the media file can move from let's say 5 dB to 110 dB at 4 kHz, without distortion.

With a DAC an amplifier with let's say 115 dB SNR, with the volume control fixed.

It seems to me like the 6 dB per bit rule is defined by quantization noise.

SNR in ADCs: Where did all the bits go? | EDN-

"All ADCs generate quantization noise as a consequence of dividing the input signal into discrete “buckets.” The ideal width of these buckets is equal to the converter’s LSB size. The uncertainty of any ADC bit is ±1/2 LSB. If you assume that this error’s response is triangular across each bit, the rms value equals this LSB signal’s magnitude divided by rms noise
Combining the rms-signal and rms-noise terms, you reach the ideal ADC SNR"


If we reduce or skip the quantization noise, then even a 4-bit / 44.1 kHz L-PCM file can achieve let's say 110 dB musical dynamic range.

The only difference is the "resolution" of the volume shifting will be much less than with a 16-bit / 44.1 kHz file.

We would perhaps hear a flat volume in the 4-bit file, when there is a quiver (fast amplitude variance) in the 16-bit file.

Is this correct?

http://en.wikipedia.org/wiki/Tremolo

Vibrato - Wikipedia, the free encyclopedia

 

[Kastor L]

It does inside the digital system.
///
To make this clear, I've made 2 soundfiles with my DAW.
///
To hear the soundfiles change zip to wav.

I will try your files later with a slow roll-off filter versus a fast roll-off filter, that should yield some difference right?