Roots of sum of factorized polynomials?

[jcx]

oh thats different, try Kharitonov + Robust Control

"The problem of robustness under parametric uncertainty received a shot in the arm in the form of Kharitonov's Theorem for interval polynomials, which appeared in the mid-1980's in the Western literature. It was originally published in 1978 in a Russian journal. With this surprising theorem the entire field of robust control under real parametric uncertainty came alive and it can be said that Kharitonov's Theorem is the most important occurrence in this area after the development of the Routh-Hurwitz criterion. A significant development following Kharitonov's Theorem was the calculation, in 1985, by Soh, Berger and Dabke of the radius of the stability ball in the space of coefficients of a polynomial.

From the mid-1980's rapid and spectacular developments have taken place in this field. As a result we now have a rigorous, coherent, and comprehensive theory to deal directly and effectively with real parameter uncertainty in control systems. This theory nicely complements the optimal theories as well as Classical Control and considerably extends the range of possibilities available to the control specialist.
"
from
http://portal.acm.org/citation.cfm?id=545947

lots of refs in google

also Middlebrook's extra element theorem approach developed in
Vorperian's "Fast Analytical Techinques for electrical and electronic circuits"
http://www.powells.com/biblio?show=HARDCOVER:SALE:9780521624428:68.00

http://www.consult-cpr.com/Additional Pages/Eng LinksC.html

 

[jcx]

the Bhattacharyya book is downloadable:

http://www.ece.tamu.edu/~bhatt/

 

[Christer]

the Bhattacharyya book is downloadable:

http://www.ece.tamu.edu/~bhatt/

Great, thanks. I'll have a look at it to see if I understand anything of it.

 

[PigletsDad]

There is one trivial, but important special case.

If any factors are present in both polynomials, they will form factors of the sum, and the sum can be written as the product of shared factors and the sum of the product of the other factors. If this happens in your case, it may reduce the degree of the remaining factorisation to one which you can make progress with.

If you don't have common factors, analytic progress is pretty limited except for low degrees.

Numerical methods are pretty good; I seem to remember there are routines in the NAG library for this sort of stuff, and I expect Mathematica etc can do it as well.

 

[jcx]

you could take a geometric pole/zero view

seperate and then divide through to get

A(s)/B(s) = -1

then you could plot the | A(s)/B(s) | = 1 contours

and the Arg( A(s)/B(s) ) = pi isolines

their intersections are the roots of the summed polynomials, less the common roots which cancel in the division - of course the common roots are roots of the final sum too

computation wize this may not be a win but it should help in visualizing the relation of the roots of the sum to the starting polynomial's individual roots

there are likely lots of conformal mapping/compelx analysis ideas that come in to play that I've mostly never learned or forgot

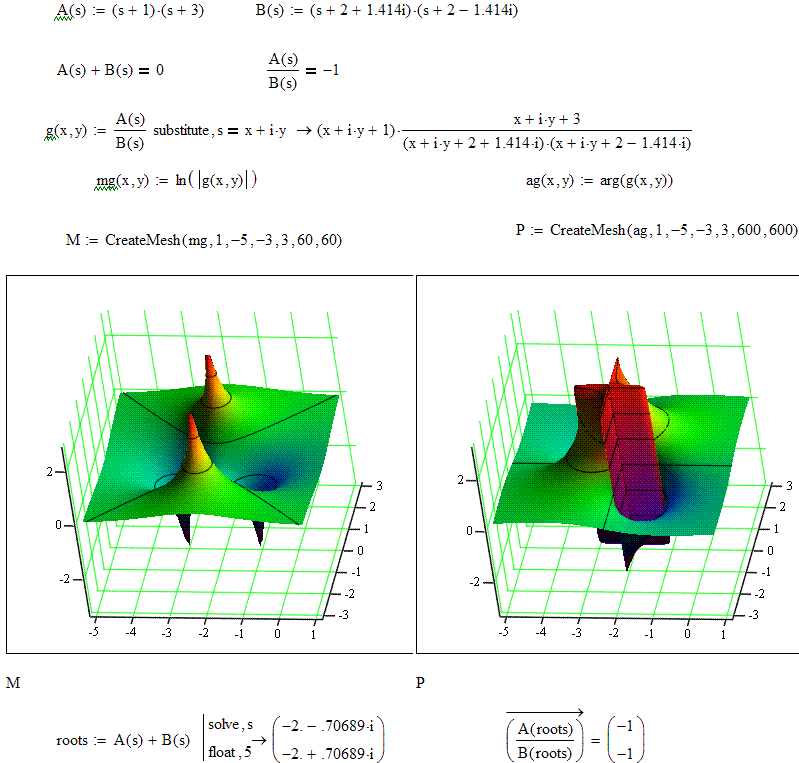
here I followed the above concept, but plotted ln(|g(s)|) - the poles and zeroes are more equally weighted by the log display, the ln(*) = 0 is of course the |*|= 1 locus, which is the hyperbolic appearing black contour line in the 1st plot

the phase surface is harder to interpret, there is a discontinuity where the arg function wraps from +pi to - pi, the intersections of these "tears" in the phase sheet with the 0 ln(magnitude) locus in the 1st plot are the locations of the roots of the sum of the polynomials

the phase wrap discontinuities connect poles with zeros in a conjugate symmetry preserving (minimal? ) set of phase isolines, this shows how the roots of the summed polynomial will be constrained to be "between" the pairs of roots of the A(s), B(s) starting polynomials

when the degree of A(s), B(s) are not equal, the "excess" poles or zeros in the ratio plot will be paired to the zeros or poles at infinity and be "connected" by a +/-pi phase wrap line to the paired infinity points, this indicates that "excess" roots in either A(s) or B(s) will be pushed away from the region of paired roots

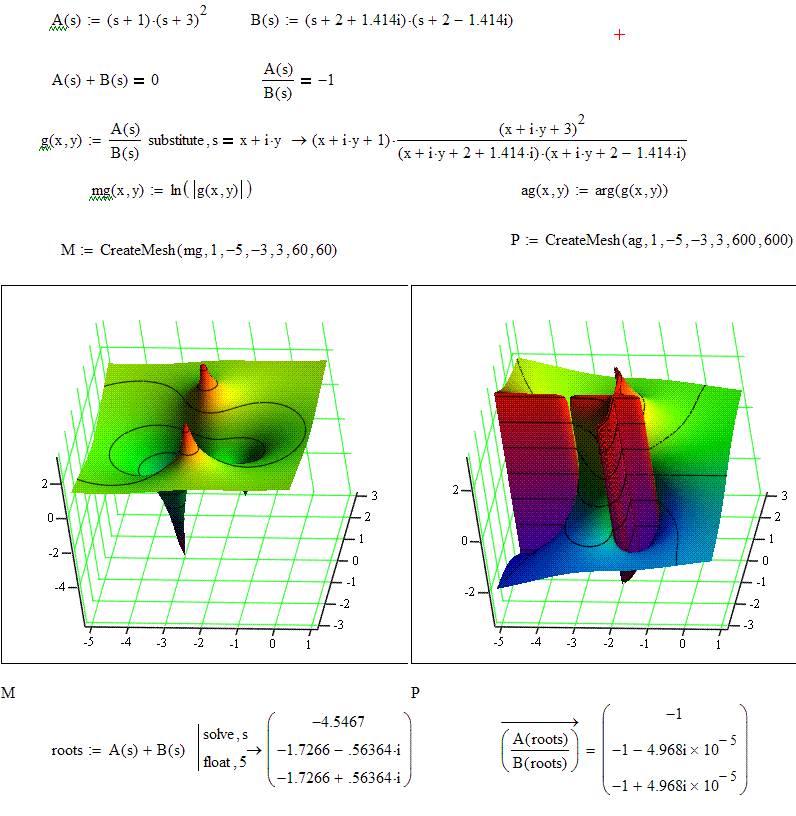
2nd pic:

this illustrates the pushing away of an "excess" root in A(s) vs the degree of B(s) - everything in the same positions/scale as the 1st plot, but the A(s) root (s+3) is squared giving a double zero in the A(s)/B(s) pole-zero surface

i think you can see the phase discontinuity ridge from the excess (s+3) heading out to its "paired" pole at -infinity on the left of the phase plot
numerically we now have a root at -4.5 in the summed polynomial wihich is "outside" of the region containing the A(s), B(s) roots